ARTIGO ORIGINAL
OLIVEIRA, Miguel Araújo [1]
OLIVEIRA, Miguel Araújo. Aproximações para Enésimo Número Primo. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 12, Vol. 06, pp. 64-72. Dezembro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/enesimo-numero, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/enesimo-numero
RESUMO
Este artigo tem como principal objetivo apresentar uma fórmula algorítmica para calcular o enésimo número primo. Tal fórmula é essencial para partirmos do estado inicial para algum algoritmo mais desenvolvido no futuro. Grandes matemáticos deixaram suas pequenas e grandes descobertas, algumas podendo servir de suporte para a fórmula que será apresentada neste material. Futuramente, esse material pode ser usado para o progresso nos estudos relacionados à teoria dos números podendo enfim, concluirmos uma fórmula fechada para o termo primo geral. Cada contribuição é importante. Logo, todos os pequenos avanços nos fazem chegar mais próximos daquilo que realmente queremos alcançar. Dada a fórmula presente neste artigo, é de suma importância o total compreendimento para que futuros matemáticos possam tomar como inspiração do desenvolvimento possivelmente precoce após essa descoberta. Atribuído de todo o conhecimento sobre a definição de números primos, esse trabalho apresentará uma demonstração da fórmula podendo facilmente ser interpretada pelo leitor.
Palavras-Chave: Fórmula, enésimo termo, número primo.
INTRODUÇÃO
As sequências possuem padrões definidos. Alguns padrões são difíceis de encontrar, como por exemplo: 2, 8,666…, 10,888…, 11,6296296296…, 11,8765432099…, e assim por diante. O segredo por trás dessa sequência é:
onde a1 é o primeiro termo da sequência.
⅔+8 = 8,666… , 8,666…/3+8 = 10,888… e assim por diante.
A sequência dos números naturais obedece uma regra simples. (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … ). Observe que essa sequência aumenta de 1 em 1 conforme prossegue.
Veja que a equação nesse dois exemplos funciona para todos os termos da sequência se porventura funcionar para o primeiro. Verificando que a sequência é (1,2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … ) vemos que, a1 = 1, logo 1 + 1 = 2. Considerando 2 como a1, temos 2 + 1 = 3, e assim por diante. Nesses casos é muito simples definirmos o modelo que rege a sequência. Mas, se tratando de números primos o segredo é quase impossível de ser desvendado.
APROXIMAÇÕES PARA SEQUÊNCIAS SIMPLES
A sequência dos números pares e ímpares é bem interessante, pois as duas consiste na soma de 2 números em relação aos 2 primeiros. Assim como visto no exemplo anterior, podemos modificar o modo com que encontramos os valores da sequência. Exemplo:
Os números pares; (0, 2, 4, 6, 8, 10, 12, … ), observe que a regra por trás dessa sequência é:
pois, se a1 for 0, então 0 + 2 = 2, dado um novo a1 = 2, temos 2 + 2 = 4, e assim por diante. Mas, observe que temos outra forma para determinar os elementos dessa sequência:
dessa forma, usando as regras de arredondamento, podemos determinar os valores pares da sequência.
a1 + 51/30 com a1 = 0, temos 0 + 59/30 = 1,9666…, arredondando 1,9666… para inteiro, temos 2. Dado a1 = 2, temos 2 + 59/30 = 3,9666…, arredondando 3,9666… para inteiro, temos 4. Esse algorítmico serve para definir qualquer sucessor par, como por exemplo o número par depois de 12563456. Dado a1 = 12563456, temos 12563456 + 59/30 = 12563457,9666…, arredondando 12563457,9666… para inteiro, temos 12563458.
TERMO GERAL DE UMA PROGRESSÃO ARITMÉTICA
Com base no que já foi apresentado até aqui, podemos também determinar o enésimo termo de uma sequência. Dada a sequência dos números pares a seguir:
0, 2, 4, 6, 8, 10, 12, …
sabemos que o primeiro termo dessa sequência é 0, o segundo termo é 2, o terceiro termo é 4, o quarto termo é 6, e assim por diante. Mas, qual a regra por trás disso? Como podemos saber qual o quadragésimo oitavo termo dessa sequência sem ficar somando de 2 em 2 até chegarmos na resposta?
 onde n é a posição do termo que queremos encontrar, nesse caso o 48° é n = 48, então 2 x 48 = 96, então 96 é quadragésimo oitavo termo da sequência dos números pares.
onde n é a posição do termo que queremos encontrar, nesse caso o 48° é n = 48, então 2 x 48 = 96, então 96 é quadragésimo oitavo termo da sequência dos números pares.
Por conseguinte, as sequências cuja possuem uma razão ≠ 2, temos a seguinte fórmula criada por Carl Friedrich Gauss (1777-1885).
onde an é termo geral a ser descoberto, a1 é o primeiro termo da sequência, n é a posição do termo geral e r a ordem de distribuição da sequência conhecida com razão. Vamos a um exemplo:
Dada a sequência (0, 3, 6, 9, 12, 15, 18, 21, …), sabemos que o primeiro termo é 0, o segundo termo é 3, o terceiro termo é 6 e logo percebemos que a ordem de distribuição é de 3 em 3, sabendo esses dados qual seria o milésimo sexto termo dessa sequência?
an = a1 + (n – 1) . r
an = 0 + (1006 – 1) . 3
an = 0 + (1005) . 3
an = 0 + 3015
an = 3015
Concluímos que, 3015 é o 1006° termo dessa sequência. No entanto, há sequências praticamente impossíveis de determinarmos sua razão, tornando muito difícil encontrar seu termo geral ou enésimo valor. Como exemplo temos a sequência dos números primos.
NÚMEROS PRIMOS
Os números primos são os átomos da Matemática, quando um número não é primo ele é composto por primos. Há casos quando um número não é nem primo e nem composto, como é caso dos números binários. Toda essa relação tem uma sintonia fina matemática por trás da aura do Universo. Cabe aos matemáticos descobrirem o que regem tais leis e determinar suas regras para fins evolutivos em espécie. Sabemos que os números primos estão aí, mas o que não sabemos é qual fórmula gera números primos. O principal intuito desse artigo é apresentar um algorítmico formular que consiste no encontro do termo geral primo.
Observando a sequência a seguir, vemos a beleza como que esses números se comportam:
2, 3, 5, 7, 11, 13, 17, 19, 23, …
observe que, é praticamente impossível descobrir sua ordem de propagação. Veja que a razão entre os dois primeiros termos é 1, já a razão entre o quarto e quinto é 4. É evidente que a razão é particular em cada um dos casos, logo não podemos usar a fórmula de Gauss para determinar o termo geral dessa sequência.
ENÉSIMO TERMO PRIMO
A fórmula aproximada para a sequência dos números primos que será apresentada agora, é relativa ao modelo usado na “aproximação para sequências simples”. No entanto temos
Chamaremos “piso de w” a parte inteira de w, usando o símbolo ?. Portanto, o termo geral da sequência de números primos fica assim
sabendo que o arredondamento de ?(w) é par, o enésimo primo será o arredondamento de ?(w), mais 1.
Veja este exemplo para n = 8:
Lembre-se que, relacionado a sequência de números pares, estamos bem próximos de descobrirmos um padrão para a sequência dos primos. Às vezes o valor de an não é tão próximo do valor, às vezes, conseguimos gerar primos de outras casas e por vezes a sua parte inteira é o primo em si. O mais lindo nisso tudo é que com essa visão podemos futuramente desvendar a fórmula fechada para números primos. Dentre alguns dos exemplos que pode acontecer com o valor de an citado temos um exemplo simples. Usando essa fórmula de aproximação para sequências, vamos calcular o quinto e milésimo número primo. Assim, temos
an = 10π^0,9595…/ 3 ⇨ 9,9975606656 arredondando para inteiro temos an = 10. Lembre-se que, se arredondamento de ?(w) for par, então o valor de an=10+1. Logo, concluímos nesse exemplo que, o quinto número primo é 11.
Para n = 1000 usamos o mesmo processo com as mesmas regras e corolários. No entanto, é de suma importância fazermos os cálculos detalhadamente para não concluirmos o valor do n ésimo primo errado quando se trata de termos gerais grandes como vamos verificar no próximo:
an = 7921π0,9595…/3 ⇨ 7919,0678032296 arredondando para inteiro, temos an = 7919.
METODOLOGIA
Usa-se o maior número de dados possíveis para podermos definir um padrão. No entanto, o padrão real é quase que impossível. Porém, com pesquisas e com muito esforço conseguimos chegar ainda mais perto no que desejamos.
Verificamos que existem diversas fórmulas que nos mostram a aproximação para números primos. Todas elas em algum dia serão realmente úteis. Dentre estas fórmulas, temos
- FÓRMULA DE APROXIMAÇÃO PARA ENÉSIMO PRIMO ASSÍNTOTA.
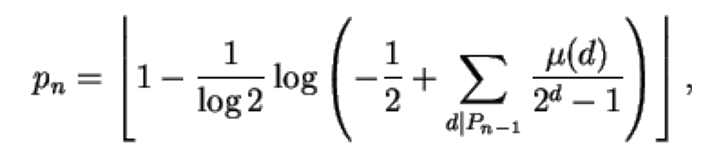
Entendendo e absorvendo a aura de todas essas fórmulas, podemos criar uma nova, ainda mais próxima, para desvendar esse mistério. Contudo, a fórmula apresentada neste é graficamente, um pequeno avanço na compreensão dos números primos.
RESULTADOS E DISCUSSÃO
Este artigo apresentou uma forma de calcular o enésimo número primo. Tal forma é essencial para partirmos do estado inicial para algum algoritmo mais desenvolvido no futuro. Grandes matemáticos deixaram suas pequenas e grandes descobertas, algumas podendo servir de suporte para a fórmula que fora apresentada neste material. Futuramente, esse material pode ser usado para o progresso nos estudos relacionados à teoria dos números podendo enfim, concluirmos uma fórmula fechada para o termo primo geral. Cada contribuição é importante. Logo, todos os pequenos avanços nos fazem chegar mais próximos daquilo que realmente queremos alcançar.
Observe que, em nosso primeiro exemplo dos números pares o algorítmico que foi apresentado pode nos dar com precisão o número par, o que falta é descobrir o modelo por trás da sequência dos primos. Acredito que o modelo apresentado neste artigo pode ajudar no avanço da compreensão do real mistério que envolve os números primos.
Dada a fórmula presente neste artigo, é de suma importância o total compreendimento para que futuros matemáticos possam tomar como inspiração do desenvolvimento possivelmente precoce após essa descoberta. Atribuído de todo o conhecimento sobre a definição de números primos, esse trabalho apresentará uma demonstração da fórmula podendo facilmente ser interpretada pelo leitor.
DEMONSTRAÇÃO PARA PARTE INTEIRA DE ?(W)
Dado n=1, temos an=2. Se o piso de [0,904554885-( 0,904554885√0,6348 )+√5 ]=2 quando n vale 1, então n ∈ IR. Logo a imagem de f(k)={k-[ k√0,6348 ]+√5} tem parte inteira um número primo, ∀ n ∈ IP.
FUNDAMENTAÇÃO TEÓRICA E CONSIDERAÇÕES FINAIS
Sabemos que os números primos são infinitos e que qualquer descoberta voltada para um avanço significativo relativo aos números primos é de suma importância e gera prêmios e etc. No entanto, o principal foco desse artigo é avançar milimetricamente nesse campo contribuindo ativamente para sua compreensão assim como foi usado exemplo dos números pares a1+59/30.
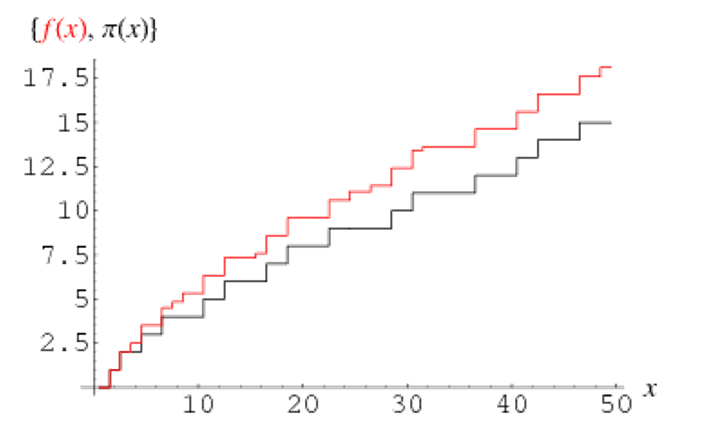
Existe uma fórmula assintótica para encontrarmos os primos, com base nessa fórmula foi realizada alguns estudos no passado para entender o comportamento gráfico dos números primos. Um de seus principais mistérios é seu comportamento gráfico.
- FUNÇÃO π(x), PARA X ∈
REFERÊNCIAS
FÓRMULAS PARA PRIMOS E TESTE DE PRIMALIDADE: Disponível em: <http://www.mat.puc-rio.br/~nicolau/papers/mersenne/node18.html>.
FUNÇÃO PARTE INTEIRA: Disponível em: <https://olimpedia.fandom.com/pt-br/wiki/Fun%C3%A7%C3%A3o_Parte_Inteira#:~:text=A%20parte%20inteira%20de%20um,com%20%22arredondar%20para%20baixo%22.>.
FUNÇÃO DE CONTAGEM: Disponível em: <https://www.google.com/url?sa=i&url=https%3A%2F%2Fmathworld.wolfram.com%2FRiemannPrimeCountingFunction.html&psig=AOvVaw0Wicgsmc2kX-YQ6vKBBYlH&ust=1602798217788000&source=images&cd=vfe&ved=0CA0QjhxqFwoTCPC8g6j5iOwCFQAAAAAdAAAAABAJ>.
NÚMERO PRIMO. In: WIKIPÉDIA: a enciclopédia livre. Wikipédia, 2020. Disponível em: <https://pt.wikipedia.org/wiki/N%C3%BAmero_primo>.
SÓ MATEMÁTICA: “Progressões” em Só Matemática. Virtuous Tecnologia da Informação, 1998-2020. Consultado em 14/10/2020 às 13:58. Disponível na Internet em: <https://www.somatematica.com.br/emedio/pa/pa3.php>.
BIOGRAFIA DE RIEMANN: Disponível em: <https://pt.wikipedia.org/wiki/Bernhard_Riemann>.
APÊNDICE – REFERÊNCIA DE NOTA DE RODAPÉ
2. Disponível em: https://www.google.com/url?sa=i&url=https%3A%2F%2Fmathworld.wolfram.com%2FRiemannPrimeCountingFunction.html&psig=AOvVaw0Wicgsmc2kX-YQ6vKBBYlH&ust=1602798217788000&source=images&cd=vfe&ved=0CA0QjhxqFwoTCPC8g6j5iOwCFQAAAAAdAAAAABAJ
[1] Estudante de Licenciatura em Matemática no Centro Universitário Leonardo da Vinci, Técnico em Auxiliar administrativo pelo Instituto Federal do Pará. Vínculo com Centro Universitário Leonardo da Vinci.
Enviado: Outubro, 2020.
Aprovado: Novembro, 2020.
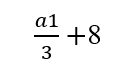


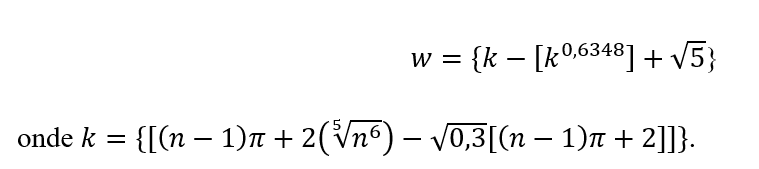
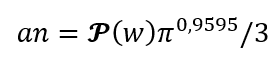

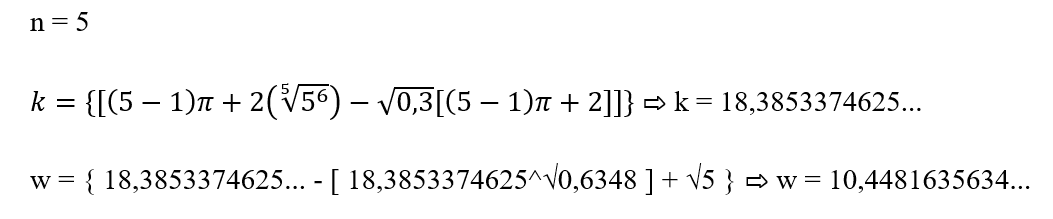
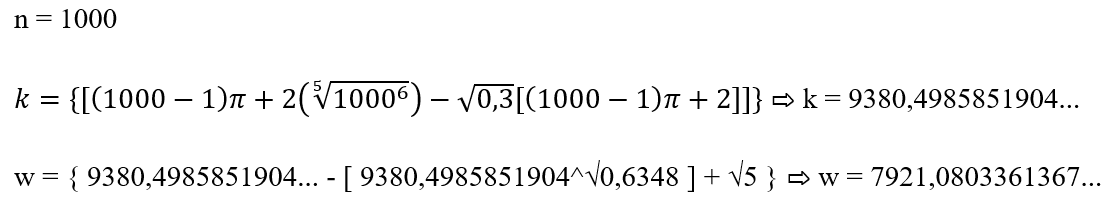


7 respostas
Parabéns pela conquista guerreiro, vc vai longe com sua dedicação e inteligência
???
Gostei bastante do artigo! Bom para entendedores e leigos em matematica! Parabéns aos envolvidos
Muito bom o seu artigo mano, muito sucesso aí!
Prezado Sr Miguel Araújo Oliveira, interessante sua explanação e demonstração, peço minhas sinceras desculpas a todos(as) aqui presente desta Revista Científica, dentro de sua explanação e demonstração encontrei alguns pontos negativos ao afirmar que existe números primos gêmeos!!! com base em suas fórmulas apresentada na inicial: “Eis a definição da função de contagem dos números primos, até um certo número x Equação”, prove com números sua afirmação os números primos gêmeos e qual o valor de π usado em suas demonstrações?; como já é sabido de tempos passados que este enigmático número de π , conforme relato do grande pensador e matemático Arquimedes de Siracusa, “No que diz respeito à obtenção do número, estima-se que em 250 A.E.C.(Antes Era de Cristo); Arquimedes obteve uma aproximação de π calculando o perímetro de dois hexágonos, um inscrito e outro circunscrito numa circunferência. Ao aumentar o número de lados do polígono, até chegar aos 96 lados, conseguiu uma aproximação igual a esta fração de números inteiros(22:7=3,1428571428571428571428571428571)”(Fonte site de Matemáticas), de tempos passados ele foi dito como um número transcendente e irracional, ocorre que um Brasileiro com um Polígono de 1134 lados dentro de uma Circunferência de 360º graus obteve uma razão de números inteiros, afirmando cientificamente com uma obra cientifica publicada: ” A ousadia do π ser racional”. que na era atual padronizou este enigmático número de π para ser Racional e Irreversível(3,15), Três inteiros e quinze centésimos finito depois da vírgula, dentro deste número enigmático com 100% de total precisão, sancionei uma lei que deverá ser respeitada sempre, está Lei diz: “Não pode ser aproximado, Não pode ser arredondado, Não pode ser simplificado, Não pode ser Fatorado; tem que ser 100% exato com total precisão” nas resoluções onde ele estiver presente…. com relação aos números primos, onde um Brasileiro afirma cientificamente que alguns números não são primos como todos(as) vem relatando de tempos passados, com uma simples PA(Progressão Aritmética), desvendei seus enigmas, onde afirmo cientificamente que não são primos e nem primos gêmeos: segue os números relatados a seguir: 2; 19; 41; 59; 61; 79; 101; 139; 179; 181; 199; 239; 241; 281; 359; 401; 419; 421; 439; 461; 479; 499; 521; 541; 599; 601; 619; 641; 659; 661; 701; 719; 739; 761; 821; 839; 859; 881; 919; 941; 1019; 1021; 1039; 1061; 1181; 1201; 1259; 1279; 1301; 1319; 1321; 1361; 1381; 1399; 1439; 1459; 1481; 1499; 1559; 1579; 1601; 1619; 1621; 1699; 1721; 1741; 1759; 1801; 1861; 1879; 1901; 1979; e mais alguns…… sendo assim “A Hipótese de Rielmann perde totalmente sua força” o autor Sr Sidney Silva.
Prezado nobre amigo Miguel Araújo Oliveira, interessante sua pergunta, pois com uma simples PA(Progressão Aritmética) padronizei duas fórmulas: vejamos como ficaria pegar um número primo e dividir ou seja usar a fatoração ou a decomposição de números primos para ser fatorado do menor para o maior e do maior para o menor, assim será considerado um número primo:
esse número é primo 12280616105497 e somente pode ser dividido e fatorado somente pelos números 1867; 1871; 1873; 1877 que também são primos vejamos como fica minha tese:
do menor para o maior:
12280616105497 1867
6577726891 1871
3515621 1873
1877 1877
1
Agora irei fatorar com números primos do maior para o menor:
12280616105487 1877
6542683061 1873
3493157 1871
1867 1867
1
Provando minha tese que o numeral 2, 19 e outros já citados acima não são primos, e os primos gêmeos não existe. lendo este número primo teremos; (Doze Trilhões, Duzentos e Oitenta Bilhões, Seiscentos e Dezesseis Milhões, Cento e Cinco Mil Quatrocentos e Oitenta e Sete.), com esta simples fórmula cheguei na casa dos 92 Nonilhões, e é Finito…. Sr Sidney Silva.
o primeiro numero primo seria o numeral três( 3): vejamos como ficaria minha tese e teoria:
3*5*7*11*13*17= 255255 vejamos como fica pela minha definição de números primos:
Do menor para o maior:
255255 3
85085 5
17017 7
2431 11
221 13
17 17
1
Agora do maior para o menor:
255255 17
15015 13
1155 11
105 7
15 5
3 3
1
Prova que os valores fatorados somente com números primos; será considerado números primos, pois foi dividido somente com os números primos existente dentro da minha tese e teoria…porém haverá um único numero primo que será dividido por ele mesmo e o resultado será 1, classificando como os verdadeiros números primos………esse é meu conceito e a definição para os números primos…….meu cordial abraço Sr Sidney Silva.
interessante sua explanação e demonstração, simples e de fácil aprendizado aos seus alunos(as) com meu respeito a todos(as) aqui presente neste singelo canal, tenho um conceito sobre o que é números primos:
“Pra ser um número primo terá que dividir somente pelo número primo, sendo do menor para o maior, e do maior para o menor, só assim poderá ser um número primo exato e finito” essa Lei é aplicada no momento em que for feita a Fatoração ou a decomposição de números primos”…. ao contrário que todos(as) vem relatando em tempos passados, usando uma teoria já obsoleta para os tempos atuais, Sr Sidney Silva. Porém não é possível esta sequência, pois tem alguns números que não são primos e os primos gêmeos não existe…..
Parabéns pela conquista meu amigo!!!