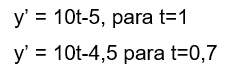Sincronizar relógios no espaço-tempo

ARTIGO ORIGINAL

LOMBARDI, Marcus Antonio ^[1]

LOMBARDI, Marcus Antonio. Sincronizar relógios no espaço-tempo. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 09, Vol. 01, pp. 107-118. Setembro de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/filosofia/sincronizar-relogios, DOI: 10.32749/nucleodoconhecimento.com.br/filosofia/sincronizar-relogios

RESUMO

Um dos pressupostos dos pesquisadores e filósofos é a capacidade de realizar questionamentos profundos constantemente. Questionamentos esses ou que sejam capazes de apontar, de provocar, ou buscar respostas para o mundo ao nosso redor. O tempo por sua vez, é um daqueles assuntos que são capazes de trazer discussões acaloradas, ou fazer parte do imaginário. Dentro deste contexto, buscando refletir sobre a sincronização dos relógios no espaço-tempo, este artigo busca teorizar sobre    a escrita matemática no início da concepção do espaço-tempo. Neste momento, encontra-se a ênfase sobre a velocidade relativa relativística representada nos diagramas de Minkowski. Através de gráficos e grandezas procurou-se compreender a validade da fórmula da velocidade relativa relativística relacionando-a com o produto interno ou soma produto de Minkowski. Em um desenvolvimento crítico posterior, buscou-se a aplicação do número e = 2,718, àqueles diagramas com vistas ao desenvolvimento de algumas propriedades do espaço-tempo, como distância espaço-temporal, gráficos, testes e problemas recentes utilizando o número e dentro dos diagramas.

Palavras-chave: Relatividade Restrita, Espaço-Tempo, Metodologia, Diagramas de Minkowski.

1. INTRODUÇÃO

Para introduzir a reflexão proposta neste estudo, é importante mencionar sobre a compreensão do real valor dos números, ou ainda, da importância desta como modo de percepção do tempo/ espaço.  O estudo “O Valor dos Números” de Pedreira (2016), sugere que, em seu início, a Aritmética tem pontos onde a notação não é inteiramente clara. Desta forma, procuramos, nesta sequência, uma crítica construtiva à notação nos inícios da Relatividade.

A Relatividade trouxe novos campos de pesquisa e focamos aqui o problema da representação dos objetos matemáticos em alguns itens da Relatividade, que se por um lado abriu fronteiras antes inimagináveis, também proporcionou questionamentos que ainda hoje não foram compreendidos.

Limitaremos a presente pesquisa a metodologia do problema básico de distância entre dois pontos, partindo da nova conceituação trazida pela Teoria da Relatividade Restrita (T.R.R.) com ênfase no espaço tempo (BOHM, 2015). Partimos da literatura tradicional e, também, de exposições veiculadas na mídia científica sobre o assunto.

Dividimos o trabalho nos itens abaixo: escrita matemática e espaço-tempo, onde se faz a retomada da demonstração da fórmula da velocidade relativa relativística em relação com o produto interno de Minkowski; a velocidade Relativa, onde desenvolvemos o tema central da sincronização de relógios no espaço tempo, primeiro recorrendo à transformação de Lorentz, e posteriormente aplicando logaritmos neperianos ao problema da sincronização dos relógios; o Cálculo nos Inícios do Espaço-Tempo, em que aplicamos o número e aos diagramas de Minkowski na teoria consagrada da queda livre revista pela teoria da relatividade restrita; sobre os diagramas de Minkowski, onde se retoma o exame dos três tipos de intervalo nos diagramas de Minkowski e se procura aplicar os conteúdos do artigo a um problema de espaço-tempo publicado recentemente pela mídia científica.

Esta construção buscou trazer os principais aspectos para construção desta teorização, sendo capaz de subsidiar até mesmo para que estudos futuros possam contribuir, ou ainda, trazer melhorias para este material.

2. ESCRITA MATEMÁTICA E ESPAÇO-TEMPO 

Retomando o artigo “O valor dos números” (PEDREIRA, 2016) há algumas operações algébricas que envolvem números negativos que pedem algum esclarecimento. Por exemplo, há alguma dificuldade em multiplicar (-5) por 2, o que é equivalente a somar (-5) vezes o número 2. A regra de sinais é suficiente para dar sequência às equações, e ainda, a experiência do matemático, irão tornar irrelevante tal questionamento.

Também, o sinal (-) tanto indica que o número é negativo, quanto a operação subtração, e outras notações como o sinal (-) nos logaritmos podem não ter inteira clareza, mas ficam resolvidos pelo matemático experiente.

Mas a dificuldade se mantém se aproximarmos as notações algébricas das equações da física. Há problemas difíceis nos dois campos do saber, e algo como uma boa solução foi apresentado nos estudos de Popper (2007), décadas atrás. Podemos salientar deles a falseabilidade e a pesquisa interdisciplinar, iniciativas hoje bastante divulgadas.

Seguimos aqui essa via construtiva inaugurada por Popper (207), pesquisando itens da escrita algébrica que podem ser aperfeiçoados tendo em vista sobretudo os diagramas de Minkowski.

Começamos retomando algo daqueles inícios da Relatividade. Ela foi posta em diagramas da geometria analítica. Era inevitável esse expediente, mas o espaço-tempo quadridimensional não se encaixa perfeitamente naquela geometria. Surgem as geometrias do espaço-tempo, e é nessa mudança de metodologia que concentramos estas pesquisas, com foco em algumas passagens algébricas.

Hoje já é mais familiar a todos nós os resultados contraintuitivos da teoria, como alguém em movimento contar espaços e tempos diversos de alguém estacionário, x/x’= t’/t.

Os diagramas de Minkowski são sempre citados porque facilitam a compreensão de que a velocidade da luz, c, é a medida que relaciona os espaços e os tempos dos observadores em movimento, contração do espaço, dilatação do tempo.

Vamos comparar a representação do movimento na antiga teoria e na Relatividade.

Temos a adição de velocidades, 4+4=8, no espaço tridimensional. Já no espaço-tempo, , em acordo com a adição relativística de velocidades.

Um dado notável é que alguém entre dois móveis que viajam a v, em sentidos opostos, contava 0 de v relativa, conta agora pouco mais de v, na nova teoria, mas 2v não ultrapassa o valor de c.

Há uma complicação no espaço-tempo que não havia antes: aquela representação natural de comparar um movimento no espaço como a diagonal de um cubo, é substituída pelo produto interno de Minkowski, principalmente:

(u + v, w) = (u,w) +(v,w)

Podemos associar o v às três coordenadas espaciais da antiga teoria e o w à correspondente coordenada temporal de v. O v e o u somados e a diagonal de um retângulo, e os lados, ou projeções somadas dão a velocidade relativa, maior que a diagonal.

Por exemplo, , é a v. relativa.

Dois exemplos que contrariam a nossa intuição: dois raios caem, um na frente e outro na traseira do trem, ao mesmo tempo? Se um observador se movimenta no interior do vagão os eventos não são simultâneos para este observador em movimento. E, também, a velocidade relativa de dois móveis que viajam com velocidades iguais, mas em direções opostas não é igual a zero. Temos a velocidade relativa: VR = (v-v’) / 1-vv’/c˄2.[2]

3. A VELOCIDADE RELATIVA

A velocidade relativa apreendida a partir dos diagramas de Minkowski vinculados ao espaço-tempo, que inclui termos novos como linha do tempo e causalidade, propõe uma continuidade entre aqueles pontos de espaço-tempo originados nos gráficos da Transformação de Lorentz.

Há complexidade em torno da v. relativa. Na dedução da sua fórmula aparece o 1 que não constava na Transformação de Lorentz. Salientamos aqui a situação de v. relativa onde um móvel cruza com o outro, e esse ponto de encontro, o qual irá funcionar, na linguagem dos limites, como tendência a os móveis se encontrarem, encontro no espaço-tempo.

Colocando no diagrama de Minkowski o encontro desses dois móveis, um mais lento, a 0,03 c e outro mais veloz, a 0,06 c, o problema é achar os dois espaço-tempos no momento em que os móveis se encontram, sabendo que v. relativa é igual a 0,03006.

A colocação no diagrama tanto pode pôr o observador no eixo xx, e y=x, entre os dois móveis, quanto coincidindo com a saída deles. Escolhemos esta última, o móvel mais lento sai de 0, e é alcançado pelo mais veloz que saiu também de 0.

Na antiga teoria, o observador em 0 mede 0,03c (Km) quando o móvel mais lento é ultrapassado pelo mais veloz. Os viajantes no sistema 0,03c medem um espaço maior que 0,03c, e os que vão a 0,06c, um espaço maior ainda, já em acordo com a Relatividade.

Também, para alguém em 0 a ultrapassagem se deu em um segundo e a v. relativa é de 0,03c. Para o viajante, o tempo medido foi menor que um segundo, no sistema 0,03c, e menor ainda no sistema 0,06c, e a v. relativa é 0,03006c, e em acordo também com os quadrivetores e produto interno de Minkowski.

Nossa proposta é aplicar algo do cálculo a esses inícios do espaço-tempo para verificar a coerência entre conceitos utilizados e também verificar se pode haver algum ponto divergente.

Então, como sincronizar relógios de dois espaços-tempo, um a 0,03c e outro a 0,06c, sabendo que a Relatividade dá V. relativa igual a 0,03006c?

Então, alguém estacionário mede 0,03c de espaço e 1 segundo de tempo no momento do encontro. A v. relativa 0,03006 não dá a sincronia dos relógios, mas alguma indicação dela. Os espaço-tempos medidos por 0,03 e 0,06 são respectivamente 0,030015 e 0,9995; 0,03005 e 0,998; valores obtidos aplicando o fL (fator Lorentz) de 0,03c e de 0.06c, ao 0,03c de espaço e 1 segundo de tempo.

Procuramos agora a sincronização de relógios usando o número e.

A aplicação de logaritmos neperianos a sincronização dos relógios parte de que o limite quando x vai ao infinito, que resulta no número e (número de Euler ou número de Neper), tem a propriedade de 1+1/x, indicar espaço e x indicar tempo, de interesse para os inícios da Relatividade.

Aquele valor 0,03 é relacionado com o número e, assim, e , e usamos aqui a função , inversa de ln, da calculadora do celular. Transcorrido um tempo de 1, exp(1) = 2,718, transcorrido um tempo de 0,03, exp (0,03) = 1,0304. O 0,03, é tomado como medida de tempo, em relação com o 1, 1 segundo.

Agora transcorrido um tempo 1 podemos associá-lo a c, transcorrido um tempo menor, 0,03 segundos ele se associa a uma parte de c, que no exemplo acima vale 1,0304. Mas aqui a parte é maior do que 1, mas um tempo transcorrido de 0,06 segundos, também será associado a um valor maior que um, mas maior que 1,0304, ele vale e e guardam proporção, como também e.

Fazemos então c equivalente a e, aproximação a menor, e fica ln c=1 e podemos monitorar o encontro dos móveis em 0,03006c.

Quer dizer, o viajante de 0,03c, parte de sua origem remota e chega, após t segundos a 0,03006c, e o viajante de 0,06c, lá chega após t’ segundos, mas eles, t e t’, são relacionados na razão 2:

Temos e

A diferença de tempos, 1,03051 e 1,03045 = 0,0006 dá conta de que os viajantes partindo ambos da origem remota, passam ou percorrem o espaço 0,03c e avançam a 0,03006c, e a diferença de logaritmos 0,0006, indicadora de tempos transcorridos é avaliada diversamente por 0,03 e por 0,06, na razão 2.

Então o logaritmo 1,03051, já é revisto pelo fator de Lorentz

O tempo em segundos, que se deve gastar para ir a 0,03 é 1,03045, calculado a maior (deveria ser igual a 1) segundo o observador o estacionário. O tempo é 1,03051, para o viajante 0,03 e também para o viajante 0,06, também calculado a maior; este reclama 1/3 de 0,0006, igual a 0,0002, porque gasta tempo menor, e os 2/3 de 0,0006 cabem ao viajante 0,03. Fica tempo de 0,03=1,03045+0,0004, e tempo de 0,06=1,03065+0,0002. O inverso desses valores dá o espaço, como é inverso, é calculado a menor.

E chegamos aos pares, começando pelo tempo, temos o tempo de 0,03, 1,03085, que forma o par com 0,03 vezes o inverso de 1,03085, que resulta 0,0291021. E o par 1,03065, que resulta 0,029107, valores bem próximos do cálculo exato, mas com alguma contradição, porque é contado um tempo maior do que aquele de um observador estacionário.

4. O CÁLCULO NOS INÍCIOS DO ESPAÇO-TEMPO 

A praticidade dos diagramas de Minkowski permitiu a esse Autor avançar no cálculo aplicado ao espaço-tempo, por exemplo, o tempo próprio e o tempo que vai de um Evento,  a outro evento medido pelo relógio de um observador que segue uma determinada trajetória de  a  O valor obtido depende não só dos dois eventos como também da trajetória seguida; ele é maior o quanto possível quando medido por um observador que se desloca em movimento retilíneo uniforme.

Observamos que o Autor incluiu a integral na equação do tempo, em algumas passagens algébricas, e esse uso do cálculo feito pelo Autor, seguimos também, mas com interesse em comparar a antiga e nova teoria.

Pesquisamos então, a escrita de fórmulas ou dados importantes como a queda livre e o número e, no contexto do espaço-tempo. Começamos com um dado conhecido. Por exemplo, determinar qual é o tempo em que o objeto em queda livre atinge a metade da trajetória. Pondo , no tempo de 1 segundo à meia trajetória fica e tempo = 0,7 segundos.

Agora o motivo da pesquisa da v. relativa foi chegar a corresponder os achados a escala de logaritmos, e os achados ficam como tendência a, ou limites de. Aqui, também a equação de Torricelli fica como campo de aproximação aos logaritmos naturais, pensando por exemplo em uma queda livre meio infinito, e/2. Parece que há, nos diagramas, a exigência de corresponder a escrita da antiga métrica à nova, fixando-se antes nos dados consagrados das antigas teorias. A métrica não se separa da física, em muitas pesquisas do autor, e estas somente vemos com maior interesse.

Nessa associação de logaritmos e queda livre, retomamos aquele valor acima de 0,7 segundos com vista a igualar uma queda livre com a medida a e.

Nesse contexto novamente ocorreu a proximidade da antiga teoria com a nova, e o cálculo dá às vezes medidas próximas e às vezes não, mas não é tarefa fácil vincular a experiência ao espaço-tempo. Os viajantes não compartilham um mesmo conjunto de eventos como vimos acima. Eles avaliam espaços-tempo que não coincidem nem no tempo e nem no espaço, diverso da antiga teoria.

Bem, o 0,7 segundos está na antiga teoria e visualizamos bem as derivadas primeira, velocidade instantânea, e segunda, aceleração, da primitiva, espaço, no exercício que fizemos acima.

Vamos fixar bem esse resultado.

A primitiva é , a primeira derivada, 10t, e a segunda, 10, e as grandezas são metro, metro por segundo e metro por segundo ao quadrado. Aquele 0,7 acima, ajuda a calcular o b, da equação ax + b, tangente à parábola , e fica no contexto algébrico bem coerente da antiga teoria:

Aproximando agora esses achados do número e. Como fica o extremo de xx, se o extremo de yy é e, e onde colocamos e/2?

O problema, praticamente de incluir o número e nos diagramas de Minkowski, envolve as pesquisas recentes sobre este número.

Encontramos a informação , mas não localizamos a demonstração desta fórmula.

Passamos ao número e, mas em uma metodologia aproximada aos dados físicos imediatos.

Partimos da observação , o que é aceito, mas quanto aos gráficos, são dois gráficos diferentes. Assim também . Agora o 1 da fórmula é o número inteiro 1, mas representa também o mínimo e o máximo numérico.

Começamos separando os dois gráficos. Bem, as fórmulas, lim de e fazendo x tender ao infinito, dão respectivamente e , 1/e e se as sequências numéricas são vinculadas ao movimento, não coincidem.

Agora a colocação de queda livre onde a trajetória é e/2, com a intenção de por em gráfico a primitiva e as duas derivadas, fica como dependendo de como fazer o gráfico; e representa o conjunto total dos números, um número máximo. Se colocamos e na vertical e e na horizontal, ou ainda em 3d ou 4d, essas medidas ficam e/4 e nada além, e as medidas no interior do gráfico são sempre menores do que o contorno sugerido por ele. Acontece um esgotar do universo numérico.

Vamos nos fixar nesse assunto central de nossa pesquisa.

Há alguma discussão sobre a representação dos números e, e 1/e, em um mesmo gráfico. Colocando na abcissa de 0 a infinito, na ordenada, em 1, as duas funções e e 1/e coincidem, e o 1 corresponde ao tempo zero em que as funções começam a se desdobrar, de modo infinitesimal, no espaço ou gerando espaço. No limite elas alcançam e=2,72 e 1/e=0,367. E nos pontos metade de e=1,356 e metade de 1/e=0,1835, estes quatro valores indicam tempos.

Notamos que para se chegar a e se sai de zero e para se chegar a 1/e se sai do infinito numérico, e ambos, zero e infinito numérico são representados por 1 na fórmula do número e. Já o 1/x representa um infinitesimal. E leva mais tempo para compor a totalidade do que para decompô-la.

Há aqui discussão se o número 1/e se reduz a e ou é independente dele.

Retomando o exemplo acima de que a metade da queda livre ocorre no tempo 0,7 está em acordo com , medida está de tempo e 1-0,304=0,7 com boa aproximação. O 1 é a totalidade ou o mínimo de tempo e o e, totalidade de espaço ou mínimo de espaço nas situações limites.

Agora o 0,7 se refere ao lim(1+1/x) compondo do zero a e/2 e o 0,3 é o tempo da outra metade da trajetória, que é menor.

O problema de usar o lim(1-1/x) para chegar ao 0,3, decompondo da totalidade a e/2 tem solução recorrendo a construção de segmentos proporcionais.

Colocamos em uma linha o 2,72 seguido do 0,367 e construímos um triângulo com os lados 3,087, 2,72 e 1; as projeções de 0,367 e 2,72 serão bem próximas de 0,3 e 0,7, no lado igual a 1, que representa aqui a totalidade do tempo. O 0,3 é a medida da trajetória onde o móvel sai do solo em direção ao alto.

5. DIAGRAMAS DE MINKOWSKI

Nossa pesquisa em torno dos diagramas de Minkowski deve pôr em questão a conhecida dificuldade relacionada com o intervalo tipo espaço.

A dificuldade, que aparece antes dos diagramas, é que se considerarmos os três ângulos notáveis, 30, 45 e 60 graus, no primeiro a ordenada do tempo é menor que a abscissa do espaço. Vejamos bem esse ponto.

Bem vimos acima que c é medida comum de espaços e tempos medidos e vale que x/t=t’/x’, se aumentamos a medida do espaço 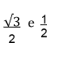diminuímos a medida do tempo. Representamos em um semicírculo c Km no eixo dos x e 1 segundo no eixo dos t (tempo). Os pontos    estão na bissetriz do diagrama, no estão no ângulo de 30 graus, e , no ângulo de 60 graus, e formam triângulos retângulos com a hipotenusa que mede 1.

Irá aparecer a palavra, intervalo, algo genérico na antiga teoria, mas aqui com a especificação, intervalo de espaço-tempo e invariante, dado pela fórmula

O problemático intervalo tipo espaço vem da definição dos três tipos de intervalo, algo impensável na antiga teoria.

“No intervalo tipo tempo, nenhuma partícula material é observada se movimentando com velocidade maior que c. As partículas sempre percorrem menor distância que a luz em intervalo de tempo fixo.

Lembrando que este intervalo tipo tempo é representado entre os ângulos 45 e 90 graus onde estão S e S’, t maior que x, compreendemos bem que em um referencial S o evento A ocorre antes de B, igualmente no referencial S’, A ocorre antes de B, delta e delta

O intervalo tipo espacial separa eventos que não podem comunicar-se entre si porque delta c delta t. A ordem no tempo dos eventos separados por um intervalo de tipo espacial depende do referencial. A ocorre antes de B em S e B ocorre antes de A em S’. (Ângulo de 0 a 30 graus) também intervalo tipo luz, nesse caso delta x = c delta t, isso corresponde a um pulso luminoso que deixa o local do primeiro evento no instante onde este ocorre e chega ao local do segundo evento no instante em que este ocorre. Estes eventos estão localizados sobre a bissetriz dos eixos x e ct. (Ângulo de 45°)” (BATISTA, 2006)

O que dizer dos movimentos que estão próximos de (1,0) além de na abcissa de espaço e em  na ordenada do tempo? Em uma primeira análise eles poderiam ser originados pelos movimentos de 45° a 90° do diagrama, mas não originam aqueles.

Nesse caso se pode ir a uma origem remota do movimento simbolizado pelo diagrama, mas além de  na ordenada de tempo e  na abcissa do espaço não se pode ir a origem 0≡0 do diagrama de espaço tempo, medidas tomadas por alguém no interior do móvel.

Em uma perspectiva interdisciplinar sugerida pelos trabalhos de Popper (2007), cabe rever esses três intervalos, com foco na análise da linguagem empregada.

Em uma segunda pesquisa nos propomos a examinar alguns pontos que ficaram sem esclarecimento: naquele exemplo de v=0,03c e v=0,06c, estamos com delta t maior que delta x, mas com v=0,8c e v=0,9c, estamos com delta t menor que delta x. Como se dá a justificação pelo produto interno nos dois casos? E também, voltando ao número e. Se este número inclui na sua definição o conjunto de todos os números maiores que zero, ele pode ser usado como eixo de um gráfico, e no outro eixo, o infinito. Também o número 1, fica ele em um eixo, e em outros dois eixos se colocam x e 1/x o que também leva a esgotar o conjunto numérico, ou pôr o infinito, sempre em um contexto metodológico do espaço-tempo.

Por fim, fica para uma segunda pesquisa um site recente da ICHI.PRO que auxilia bastante nesse conteúdo. Os personagens são Alice e Bob. Ela passa por ele a 0,5c e dispara contra ele um projétil a 0,25c. Conforme o site, a velocidade de Alice e do projétil em relação a Bob são, respectivamente: 0 e 0,2.5c; 0,21c e 0,43c; 0,5c e 0,66c. Estes resultados estão em perfeito acordo com a fórmula da velocidade relativa relativística.

Este site encontramos às vésperas desta publicação, e tem relação direta com as linhas centrais deste trabalho, mas por ora só podemos comentar: A) os autores do site não deixam claro a situação em que Bob é atingido pelo disparo e B) o tempo em que Bob se livra de ser atingido pelo disparo deve ter solução usando o número e=2,718.

6. CONCLUSÃO

A metodologia de Popper (2007) trouxe uma nova perspectiva no exame das teorias, em um contexto crítico e construtivo. Ela abre pistas para verificar melhor os termos, passagens, argumentos histórico-científicos e mesmo sociais das teorias.

Pesquisamos então algo da escrita matemática, as possibilidades de erros e os esforços para o progresso interdisciplinar, alguns temas notáveis como o uso do cálculo para testar fórmulas e construir gráficos com ênfase no espaço tempo.

Mas é Minkowski o A. que influi mais na produção deste artigo. A dedução da v. relativa posta em quadrivetores abre várias linhas de investigação para compreender melhor os inícios da Relatividade, e ao final um desafio, para uma próxima pesquisa de um melhor exame do intervalo tipo espaço, outro assunto importante deste grande autor.

REFERÊNCIAS 

BATISTA, R. C. O intervalo de espaço-Tempo. Plato – Páginas das Disciplinas – Capítulo 5: Diagramas espaço-tempo, 2006. Disponível em: http://plato.if.usp.br/~fma0374d/aula5/node7.html. Acesso em: 03 out. 2021.

BOHM, D. A teoria da relatividade restrita. São Paulo: Unesp, 2015.

EINSTEIN, A. Sobre os princípios da relatividade e suas implicações. Revista Brasileira do Ensino da Física, v. 27, n. 01, 2005. Disponível em: https://doi.org/10.1590/S1806-11172005000100005. Acesso em: 03 out. 2021.

PEDREIRA, S. M. O valor dos números. Revista Científica Multidisciplinar Núcleo do Conhecimento, ano 01, vol. 08. pp. 05-16. Setembro de 2016. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros. Acesso em: 03 out. 2021. 

POPPER, K. Lógica da Pesquisa Científica. São Paulo: Cultrix, 2007.

APÊNDICE – REFERÊNCIA NOTA DE RODAPÉ

2. Nota:

1. Sobre a demonstração usual da v. relativa há na fórmula, semelhança com a derivada do quociente, que dá margem a pensar por que aparece na demonstração v vezes o v’, em movimento retilíneo uniforme.
2. Como chegar, pelo produto interno ao valor de 11,36, que é a soma das velocidades 4 e 4?

A questão envolve o difícil conceito de inverso de uma grandeza. Se colocamos o 4 e o ¼ como segmentos, qual segmento corresponde ao 1? Porque dividindo o 4 em quatro partes, cada parte é o inverso de 4, mas multiplicando por 4, resulta uma área, ¼ vezes 4. Por aqui se vê que essa situação deve estar presente no produto interno, mas não acessamos essa fonte do autor.

O que conseguimos foi que se colocamos a 45º simétricos e opostos 4 e 4, e dizemos que vamos corresponder o segmento 4 ao quadrado 4, o segmento ¼ vai corresponder ao 1 em relação ao 16. E por fim temos 2 quadrados de 4 de lado, formando a área de 32, e não sabemos como administrar os dois quadrados, cada um medindo 1, área de 32 que dá, extraída a raiz quadrada, a metade da v. relativa, Ö32.

^[1] Doutor, Universidade Gama Filho, Departamento de Filosofia.

Enviado: Abril, 2022.

Aprovado: Setembro, 2022.