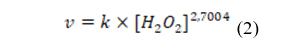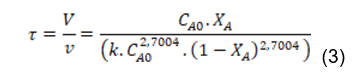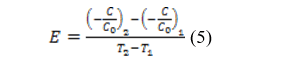ARTIGO ORIGINAL
GALLO, Gabriela [1], LEAL, Lucas Ferreira [2], D’AMELIO, Monica Tais Siqueira [3]
GALLO, Gabriela. LEAL, Lucas Ferreira. D’AMELIO, Monica Tais Siqueira. Estudo e desenvolvimento de um reator CSTR. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 10, Vol. 05, pp. 05-28. Outubro de 2019. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-quimica/estudo-e-desenvolvimento
RESUMO
A menor disponibilidade de matérias-primas tem gerado uma constante necessidade de otimização dos processos produtivos, com intuito de reduzir os custos de produção e manter a competitividade nos preços dos produtos. A partir dessa necessidade, os engenheiros são motivados a testarem várias condições de funcionamento dos processos. Como na maioria dos casos não é economicamente viável e nem seguro parar o processo produtivo a realização de experimentos no equipamento desejado, é de extrema importância o desenvolvimento de protótipos. Portanto, essa pesquisa visou estudar as variáveis que influenciam no rendimento de um protótipo de reator tanque a fim de verificar a melhor condição deste equipamento. Para tal, foi realizado o estudo da cinética a partir da reação do permanganato de potássio com o peróxido de hidrogênio, bem como, o estudo do comportamento de sistemas reais através da Determinação do Tempo de Residência (DTR). O teste 2, com volume de 925 ml e agitador de uma pá, tenha sido o que mais se aproximou de um CSTR (Reator Tanque Contínuo Ideal).
Palavras-Chave: otimização, reator CSTR, simulação de processos.
1. INTRODUÇÃO
O estudo e desenvolvimento dos Reatores Químicos são fundamentais para a produção de muitos produtos químicos industriais. Eles combinam a cinética química e o projeto de reatores para selecionar um sistema de reatores que opere de maneira mais segura e mais eficiente no processo da reação necessária. Conforme Fogler (2012), a cinética química e o projeto de reatores estão no coração de quase todos os processos químicos industriais. É, principalmente, o conhecimento da cinética química e o projeto do reator que distinguem o engenheiro químico dos outros engenheiros.
Inicialmente, deve-se entender que um processo químico envolve além de reações químicas, fenômenos de superfície e fenômenos de transporte de massa e de energia. Quando o estudo da cinética das reações químicas é feito sem considerar os efeitos de difusão de massa e de calor, gera uma diferença entre a taxa real e a taxa cinética intrínseca. Desta forma, é de extrema importância determinar alguns parâmetros para analisar o comportamento dinâmico de sistemas de Engenharia Química para visar melhorias no processo.
Assim, no curso de Engenharia Química da Universidade São Francisco – campus Itatiba, os reatores foram estudados em considerações ideais e reais através do desenvolvimento do Projeto Integrador (P.I.). O Projeto foi proposto para os alunos do 9º semestre e teve como principal objetivo a integração de conhecimentos adquiridos entre as disciplinas (Laboratório de Engenharia Química, Reatores Químicos e Termodinâmica para Engenharia Química), bem como, uma revisão orientada de todo o conteúdo do curso, por meio do desenvolvimento do reator CSTR. Entretanto, devido à importância deste assunto para os Engenheiros Químicos, neste trabalho, aprofundaram-se os estudos das condições que permitem que este, seja considerado ideal, onde os parâmetros de vazão, agitação, entre outros foram modificados e analisados.
Deve-se salientar que foi usada uma reação simples, para facilitar as medidas de concentração, uma vez que o foco principal era o reator.
1.1 REATORES IDEAIS
Os reatores químicos são equipamentos onde acontecem reações para a transformação de matérias-primas em produtos comercializáveis. Esses equipamentos existem nas mais variadas formas e tamanhos. Os tipos de reatores ideais mais comuns são: batelada (BR), tubular (PFR) e tanque contínuo (CSTR) (FOGLER, 2012).
Para a produção de um produto químico de forma economicamente viável, utilizando uma variedade de matérias-primas e uma sucessão de etapas de tratamento, é requerido o projeto de um processo químico industrial. Segundo Levenspiel (2000), de todas as etapas necessárias para a formação do produto, a etapa de tratamento químico é considerada a principal parte do processo, sendo responsável pelo seu sucesso ou fracasso.
Por este motivo, mantendo o foco no objetivo proposto por este trabalho, foram detalhadas as características de um reator CSTR, que embora não possua o maior rendimento quando comparado aos outros reatores contínuos, é usado na indústria quando uma agitação intensa é requerida.
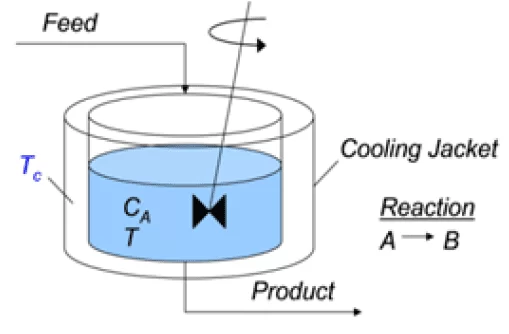
O reator CSTR possui um agitador onde os reagentes e produtos têm escoamento igual e não há acúmulo dos reagentes em seu interior, isto é, o volume é constante. Ele também é conhecido como reator de misturas perfeitas e faz com que as reações não alterem suas concentrações, velocidades e temperatura dentro do tanque (FOGLER, 2012).
Possui vantagens de controle, pois pode controlar a temperatura da reação pela regulagem da vazão de alimentação e ainda, é capaz de minimizar as reações paralelas indesejáveis através do uso de correntes com concentrações baixas de reagente limitante. No entanto, em comparação aos outros reatores que operam em sistema contínuo, apresenta a menor conversão de reagente por volume. Por isso, ele pode ser usado sozinho, ou pode ser ligado em série e em paralelo para melhorar o rendimento do processo. Para representá-lo segue a Figura 1.
Figura 1 – Reator CSTR.
1.2 REATORES REAIS
Nos sistemas reais podem acontecer desvios no sistema. É comum nestes sistemas a aproximação das equações dos reatores reais pelas equações dos reatores ideais, diminuindo consideravelmente o número de variáveis que influenciam no processo, simplificando as equações (LEVENSPIEL, 2000). Os princípios básicos de conservação de massa e energia, conforme a Primeira Lei da Termodinâmica, são os principais fenômenos considerados no equacionamento dos reatores, além das equações constitutivas, condições iniciais e de contorno (STEPHANOPOULOS, 1984).
Assim, uma forma de analisar um reator para obter resultados rápidos e seguros sem a realização de testes em uma planta real, consiste na utilização da modelagem e simulação (STEPHANOPOULOS, 1984).
A modelagem dos reatores é obtida através das leis básicas de conservação de massa e energia, consistindo primeiramente em determinar as variáveis que influenciam o funcionamento dos reatores. Estas variáveis podem ser: o volume inicial, as vazões de entrada e saída, a equação de taxa, a constante cinética, entre outras.
Para este tipo de reator, tanque, faz-se necessário o cálculo do tempo espacial. Matematicamente, é representado pela razão do volume do reator pela vazão de saída. Se o tempo espacial for igual ao tempo médio de residência, pode-se dizer que é um reator ideal, caso contrário é um reator que opera em um sistema dinâmico.
1.3 DETERMINAÇÃO DO TEMPO DE RESIDÊNCIA (DTR)
Os modelos não ideais incorporam desvios da idealidade por fenômenos de escoamento que podem ocorrer no interior dos equipamentos. Segundo Sassaki (2005), alguns fenômenos foram descritos a seguir:
- Escoamento preferencial – ocorre quando grandes quantidades do fluído escoam através do equipamento em tempo menor que outros.
- Curto Circuito: ocorre quando elementos do fluído escoam através do reator sem percorrer todo seu interior.
- Zonas Mortas: são regiões do equipamento isoladas ou inacessíveis, onde os fluídos nelas aprisionados, não interagem com a zona ativa do reator, entre outros. Desta forma, é imprescindível o conhecimento da distribuição do tempo de residência (DTR).
A DTR é uma informação que permite prever o comportamento de sistemas reais. É uma função de distribuição do tempo de residência de cada partícula, calculada através da integral, num intervalo de tempo de 0 ao ∞. O resultado obtido desta função matemática é o tempo médio de residência (SASSAKI, 2005).
O tempo de residência de uma porção ou elemento de fluído é o tempo decorrido desde a sua entrada até sua saída no equipamento. Uma vez que os diversos elementos de um fluído passam por diferentes caminhos dentro do reservatório, fica fácil perceber que terão diferentes tempos de residência (SASSAKI, 2005).
Assim, a somatória de todos estes tempos determina o tempo médio de residência do fluído. Portanto, através da curva obtida da DTR é possível prever o comportamento do escoamento de um tanque perfeitamente agitado, como pode ser observado na Figura 2 a seguir:
Figura 2 – Curvas E (Ө) para os casos de escoamento real e ideal (mistura perfeita).

2. METODOLOGIA
2.1 PROJETO E MONTAGEM DO REATOR
Este reator foi construído durante o Projeto Integrador (P.I.) através do ensino interdisciplinar das unidades curriculares do 9o semestre da Faculdade de Engenharia Química da Universidade de São Francisco, campus de Itatiba – SP, e utilizado para continuar os estudos no Trabalho de Graduação. As disciplinas envolvidas foram: Reatores Químicos, Termodinâmica para Engenharia Química e Laboratório de Engenharia Química. A Tabela 1 apresenta os materiais utilizados nesta montagem e suas dimensões.
Tabela 1- Materiais utilizados na montagem do reator CSTR.
| Materiais |
| Reservatórios de 5 litros |
| Válvulas globo ¾” em PVC |
| Cotovelos ¾” em PVC |
| Cotovelos 12 mm de engate rápido |
| Reduções de ¾” para 12 mm |
| Redução de engate rápido de 12 mm para 6 mm |
| Mangueira de Poliuretano (PU) de 6 mm |
| Tubulação de ¾” em Policloreto de Vinila (PVC) |
FONTE: Próprio autor.
A Figura 3 apresenta o reator montado com as indicações dos materiais utilizados.
Figura 3 – Montagem do reator CSTR.

2.2 DETERMINAÇÃO DA CINÉTICA DA REAÇÃO
A reação escolhida foi a de permanganato de potássio (KMnO4) com peróxido de hidrogênio (H2O2), a qual gera como produto principal o sal, dióxido de manganês, conforme descrito na Equação 1 (OLIVEIRA, 2014). Com um precipitado, é possível determinar, por proporção estequiométrica, a concentração de todos os demais componentes. Estes reagentes são fáceis de serem encontrados em farmácia e apresentam baixo custo, o que favoreceu a realização das práticas laboratoriais.
2KMnO4 + 3H2O2 ̶> 3O2 + 2H2O + KOH + 2 MnO2 (1)
2.3 ESTUDO DA CINÉTICA DA REAÇÃO E DETERMINAÇÃO DA ORDEM DA REAÇÃO
Inicialmente, prepararam-se 250 mL de soluções de:
- Permanganato de Potássio 0,1 M;
- Permanganato de Potássio 0,05 M;
- Peróxido de Hidrogênio 0,1 M;
- Peróxido de Hidrogênio 0,05 M.
As massas e os volumes usados no preparo das soluções estão indicados na Tabela 2.
Tabela 2- Composição de cada frasco utilizado para o estudo da velocidade de reação
| Reagentes | Massa (g) | Volume (mL) | Concentração (mol.L-1) |
| KMnO4 | 3,95 | 0,10 | |
| 1,97 | 0,05 | ||
| H2O2 | 19,55 | 0,10 | |
| 9,77 | 0,05 |
FONTE: Próprio autor.
Foram preparadas 9 reações. Para tal, numeraram-se os erlenmeyers de 1 a 3, conforme a composição indicada na Tabela 3. Em seguida, adicionaram-se 10 mL da solução de Permanganato de Potássio e 10 mL da solução de Peróxido de Hidrogênio, para então, cronometrar o tempo. Após, a reação, pesou-se o papel de filtro e colocou-o no kitassato para posterior filtragem na bomba a vácuo. Para cada frasco (1, 2 e 3) analisou-se a formação do produto nos tempos de 30”, 45” e 60”.
Tabela 3- Composição de cada frasco utilizado para o estudo da velocidade de reação.
| Frasco | [KMnO4] (mol.L-1) | [H2O2] (mol.L-1) |
| 1 | 0,10 | 0,10 |
| 2 | 0,10 | 0,05 |
| 3 | 0,05 | 0,01 |
FONTE: Próprio autor.
2.4 DETERMINAÇÃO DA DTR
Para o estudo da DTR foram testados 2 agitadores, o primeiro com uma pá e o segundo com mais pás, conforme a Figura 4:
Figura 4 – Modelo das pás testadas no estudo da DTR.

O traçador utilizado foi o corante alimentício da cor amarelo de tartrazina de marca Arcolor (Lote: 267648; Val: 04/2019).
2.5 CONSTRUÇÃO DA CURVA DE CALIBRAÇÃO
Para construir a curva de calibração, prepararam-se soluções de corante nas concentrações indicadas na Tabela 4 abaixo.
Tabela 4 – Valores das concentrações de corante nas amostras preparadas.
| Amostra | Concentração (g.L-1) |
| 1 | 0,8 |
| 2 | 0,6 |
| 3 | 0,4 |
| 4 | 0,2 |
| 5 | 0,0 |
FONTE: Próprio autor.
Colocaram-se as 4 soluções com corante em cubetas apropriadas para, em seguida, levarem-nas ao espectrofotômetro, onde foram medidas as absorbâncias de cada uma a 430 nm. A água pura, foi usada como branco. Após as medições realizadas no espectrofotômetro (Modelo: Bel UV – M51; Marca: BEL), anotaram-se os valores das absorbâncias lidos.
2.6 REALIZAÇÃO DA DTR
Inicialmente, calibrou-se o reator. Nesta etapa, as vazões de entrada, 60 mL.min-1, foram ajustadas à metade da vazão de saída, 120 mL.min-1, para não haver acúmulo de material. Em seguida, ajustou-se a pá do agitador a cerca da metade da altura do volume a ser utilizado e ligou-se a agitação em uma velocidade de 20 rpm.
Após o reator ficar completamente cheio, fechou-se a torneira, desligou-se o agitador e determinou-se o volume do reator através do líquido presente no reator. Esvaziou-se o tanque e encheu-o com a solução de traçador. Abriu-se a torneira para a saída de água e acionou-se o cronômetro. Retiraram-se amostras em copos de café nos tempos 0, 20”, 40”, 1’00”, 1’30”, 2’00”, 2’30”, 3’00”, 4’00”, 5’00”, 6’00”, 8’00”, 10’00”, 12’00”, 15’00”, 20’00”, 25’00”, 35’00”, 45’00”. Após a coleta, as amostras foram analisadas com auxílio do espectrofotômetro (Modelo: Bel UV – M51; Marca BEL).
2.7 DETERMINAÇÃO DA CONVERSÃO REAL DO REATOR
Para determinar a conversão do reator, inicialmente ajustaram-se as vazões para as mesmas usadas no PI. Antes de começar a reação, delimitou-se o volume de 1430 mL no reator, numeraram-se e pesaram-se os papéis de filtro e ainda, prepararam-se 2 L de soluções de permanganato de potássio 0,1 M e peróxido de hidrogênio 0,1 M. A composição das soluções está indicadas na Tabela 5. Após o preparo das soluções, estas foram colocadas nos reservatórios de alimentação. Em seguida, abriram-se as duas válvulas e aguardou-se o reator atingir o volume pré-estabelecido no início do experimento. Quando se atingiu o volume, ligou-se o agitador e abriu-se a válvula de saída. A partir deste momento, disparou-se o cronômetro e as coletas das amostras foram feitas nos tempos 0”, 1’, 2’, 3’, 4’, 5’, 6’, 7’, 8’, 9’, 10’, 11’, tempo que esvaziou os reservatórios dos reagentes. Assim, para quantificar o produto formado, as amostras foram filtradas na bomba à vácuo, separando a solução dos precipitados. Estes foram secos na estufa à 100 oC por 5 minutos, para então, serem pesados na balança analítica. Os valores da massa obtida foram anotados.
Tabela 5 – Composição de cada frasco utilizado para o estudo da velocidade de reação
| Reagentes | Massa (g) | Volume (mL) | Concentração (mol.L-1) |
| KMnO4 | 31,91 | 0,10 | |
| H2O2 | 156,31 | 0,10 |
FONTE: Próprio autor.
3. RESULTADOS E DISCUSSÃO
3.1 MONTAGEM DO REATOR
Durante o Projeto Integrador, verificou-se a necessidade de um controle minucioso em relação à vazão do reator. Para tal, as válvulas de alimentação e de saída foram modificadas. A Figura 5 apresenta as mudanças adotadas.
Figura 5 – Montagem do reator CSTR após as mudanças de melhoria no protótipo.

3.2 DETERMINAÇÃO DA ORDEM DA REAÇÃO
A partir das soluções preparadas de Permanganato de Potássio e Peróxido de Hidrogênio com diferentes concentrações, obtiveram-se as massas de precipitado.
O número de mol de MnO2 foi determinado dividindo-se a massa de precipitado encontrada pela massa molar (86,938 g.mol-1). O reagente limitante foi determinado para cada conjunto de concentrações. Assim, através da concentração molar do produto obtida, foi possível determinar as concentrações do reagente limitante.
Os valores calculados estão apresentados na Tabela 6.
Tabela 6 – Valores da massa de precipitado formado, do número de mol calculado de Produto e da Concentração do Reagente Limitante.
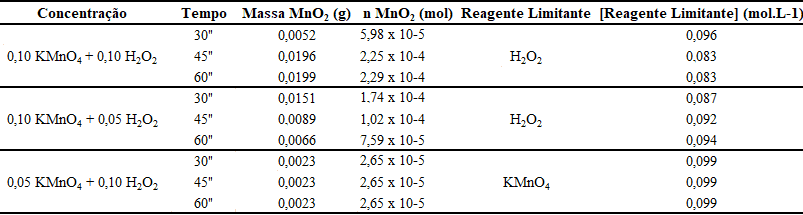
Através dos dados indicados na Tabela 6, os gráficos da Concentração Molar pelo Tempo foram construídos para cada uma das concentrações utilizadas na determinação da velocidade da reação, como podem ser observados a seguir:
Figura 6 – Gráficos da Concentração Molar do Reagente Limitante (mol.L-1) x Tempo (h).
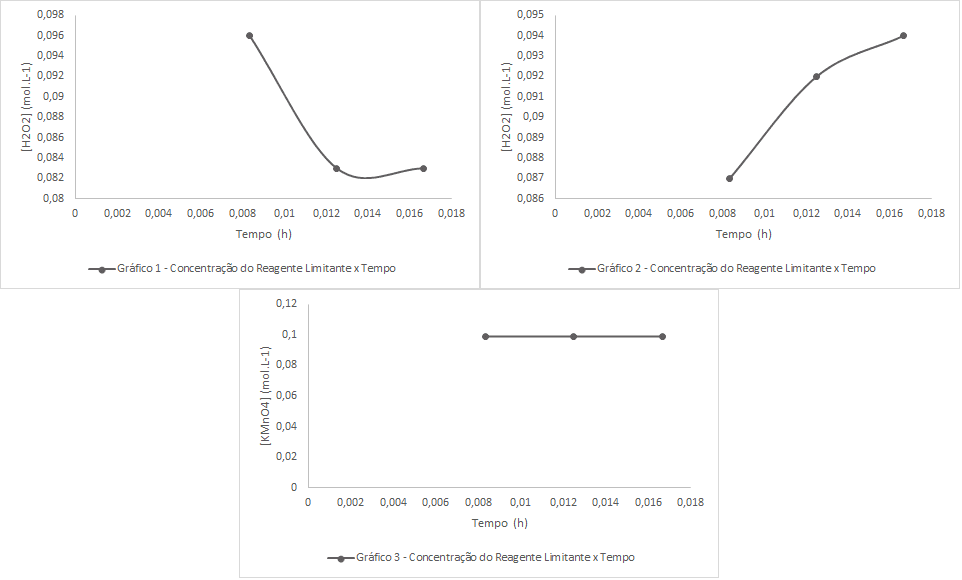
Conforme, os gráficos apresentados na Figura 6, para calcular as velocidades da reação, traçaram-se as retas tangentes a partir do primeiro ponto da curva, exceto no Gráfico 3, o qual está representado por uma reta constante. Neste gráfico a velocidade é nula. Portanto, pode-se constatar que a velocidade independe da concentração do Permanganato de Potássio. Já para os gráficos 1 e 2, as velocidades da reação foram obtidas pelo coeficiente angular da reta tangente, como podem ser verificadas na Tabela 7.
Tabela 7 – Valores das velocidades de reação calculados.
| Velocidade
(mols.(L.h)-1) |
[H2O2]
(mol. L-1) |
[KMnO4]
(mol. L-1) |
|
| -3,12 | 0,10 | 0,10 | (1) |
| 0,48 | 0,05 | 0,10 | (2) |
| 0 | 0,10 | 0,05 | (3) |
FONTE: Próprio autor.
Para determinar a ordem do Peróxido de Hidrôgenio (a), relacionou-se o primeiro com o segundo sistema. Assim foi feito também, para determinar a ordem do Permanganato de Potássio (b), porém, relacionando o primeiro com o terceiro sistema.
a = 2,7004
b = 0,00
A ordem da reação é a somatória das ordens de ambos reagentes. Como a ordem do permanganato é nula, a ordem da reação foi estabelecida a partir da ordem do peróxido de hidrogênio, a qual foi determinada em 2,7. Desta maneira, a velocidade desta reação é escrita segundo a Equação 2 a seguir:
A partir da Equação 2, determinou-se a constante cinética em 1565,3 (L/mol)2,7004.h-1.
3.3 DETERMINAÇÃO DA CONVERSÃO TEÓRICA
A determinação da conversão teórica XA foi obtida através da Equação do reator ideal. (SCHMAL, 2013)
A Tabela 8 apresenta os parâmetros do reator.
Tabela 8 – Valores dos Parâmetros do reator CSTR.
| Parâmetros do Reator CSTR | |
| Volume (V) | 1430 ml |
| Vazão (v) | 21600 ml.h-1 |
| Tempo espacial (τ) | 0,1285 h |
| Constante de velocidade (k) | 1565,3 |
| Concentração inicial (CA0) | 0,100 mol.l-1 |
FONTE: Próprio autor.
A partir dos valores da Tabela 8, foi possível resolver a Equação 3, determinando assim, o valor da conversão teórica do reator, XA = 0,528. Este valor será comparado com a conversão real para uma prévia discussão mais adiante.
3.4 DETERMINAÇÃO DA CONVERSÃO EXPERIMENTAL
Para determinar a velocidade de reação, considerou-se o estudo da DTR. Através desta consideração, com o intuito de obter a máxima conversão, escolheu-se usar o volume de reator de 1430 ml. A reação usada foi a do permanganato de potássio com o peroxido de hidrogênio, a qual obteve o precipitado de estudo. Assim, após a separação dos produtos obtidos, pesou-se a massa e calculou-se o número de mol deles, para então, determinar a concentração do reagente limitante. Como os cálculos usados foram similares aos que foram realizados na determinação da conversão teórica, de forma explicativa, analisou-se o consumo do reagente limitante ao longo do tempo através do gráfico plotado na Figura 7.
Figura 7 – Gráfico da Concentração do Regente Limitante x Tempo para determinar a conversão experimental.
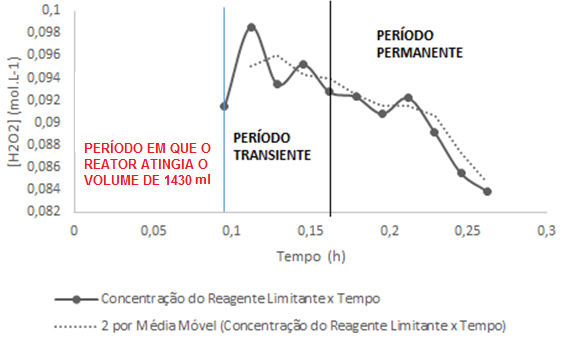
O primeiro momento do gráfico, quando não há amostras, representa o tempo que o reator despendeu para atingir o volume de 1430 mL, isto é, a válvula de saída estava fechada. Ao atingir esse volume, foi aberta a válvula de saída e o reator operou em regime transiente, ou seja, período em que a variação de concentração se encontrava de forma desordenada. O terceiro momento, mostra que o reator atingiu o regime permanente. Neste período é possível realizar os cálculos de conversão.
Portanto, para calcular a conversão experimental, considerou-se a concentração inicial, CA0 = 0,1 mol.L-1 e a concentração final, como sendo a concentração obtida no final do processo, isto é quando acabaram-se os reagente do tanque de alimentação, CAF = 0,083867814 mol.L-1.
Assim, através da Equação para determinar a conversão experimental abaixo (SCHMAL,2013), calculou-se a conversão experimental, cujo valor obtido foi de XA = 0,16132186.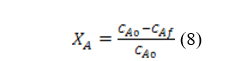
Onde, XA = Conversão do reagente limitante, CA0 = Concentração inicial do reagente limitante e CAf = Concentração final do reagente limitante.
Comparando o valor de Xa teórico (0,528) e o valor de Xa experimental (0,1613), o valor teórico apresentou-se, aproximadamente, 3,3 vezes maior que o valor experimental.
Figura 8 – Comparação da conversão teórica com a conversão experimental.

O baixo rendimento apresentado na Figura 8, é consequência das interferências provocadas pelo escoamento real, ou ainda, pela variação de volume durante a reação. Como a vazão de saída se encontrou maior que a vazão de alimentação, não se atingiu o estado estacionário do sistema e nem a condição de equilibrio para evitar a formação de vórtices.
Para verificar o quanto a não idealidade do reator influenciou na diferença da conversão, determinou-se o tempo de residência médio para comparar com o tempo espacial. Quanto maior a diferença entre eles, maior a não idealidade.
3.5 DETERMINAÇÃO DA DTR
A determinação da DTR foi feita com um traçador não reativo. Para tal, aplicou-se a técnica de estímulo e resposta. O marcador é introduzido no reator no instante t=0 e a análise da composição da corrente de saída permite conhecer a concentração do marcador na saída do reator ao longo do tempo.
Para construir a curva de calibração, mediram-se as absorbâncias das diferentes concentrações testadas no espectrofotômetro à 430 nm, conforme estão indicados na Tabela 9.
Tabela 9 – Valores das absorbâncias obtidos para a construção da curva de calibração.
| Amostra | Absorbância (UA) |
| 1 | 2,291 |
| 2 | 1,714 |
| 3 | 1,170 |
| 4 | 0,637 |
| 5 | 0,048 |
FONTE: Próprio autor.
A partir da curva de calibração traçada, determinou-se a reta de tendência, que está representada por uma função linear, cujo eixo das ordenadas é interceptado no ponto -0,0212. Como não é possível obter uma concentração negativa, necessitou-se de uma condição de contorno inicial que, estipulasse o ponto (0,0) como início da reta. Nestas condições, foi possível construir a curva de calibração ajustada conforme ilustra a Figura 9.
Figura 9 – Gráfico da Curva de Calibração à 430 nm.
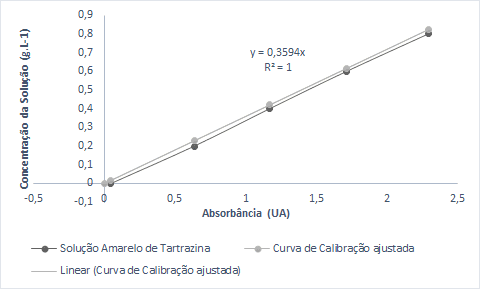
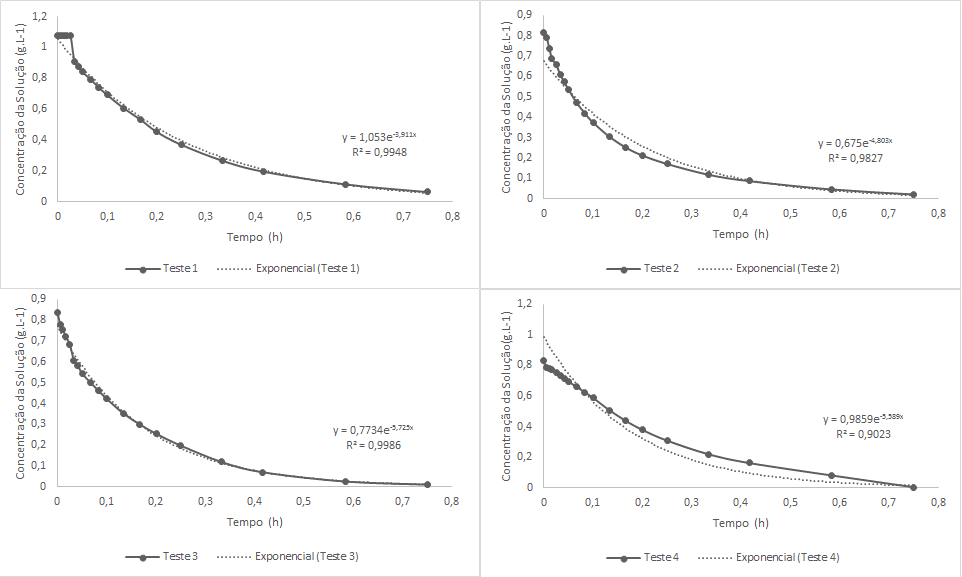
A partir da curva de calibração ajustada, determinou-se a concentração das amostras coletadas através do valor da absorbância lida na equação da reta obtida. Assim, para verificar o processo de solubilização do corante alimentício, construíram-se os gráficos da concentração da solução pelo tempo para cada teste. Nesta fase, segundo a Figura 10, constatou-se que o teste 3 foi o que obteve o melhor desempenho, uma vez que, a concentração decrescia exponencialmente conforme o desejado.
Figura 10 – Gráficos da Concentração X Tempo. a) Teste 1: Volume total com 1 pá. b) Teste 2: Meio volume com 1 pá. c) Teste 3: Meio volume com mais de uma pá. d) Teste 4: Volume total como mais de uma pá.
3.6 ESTÍMULO TIPO DEGRAU NEGATIVO
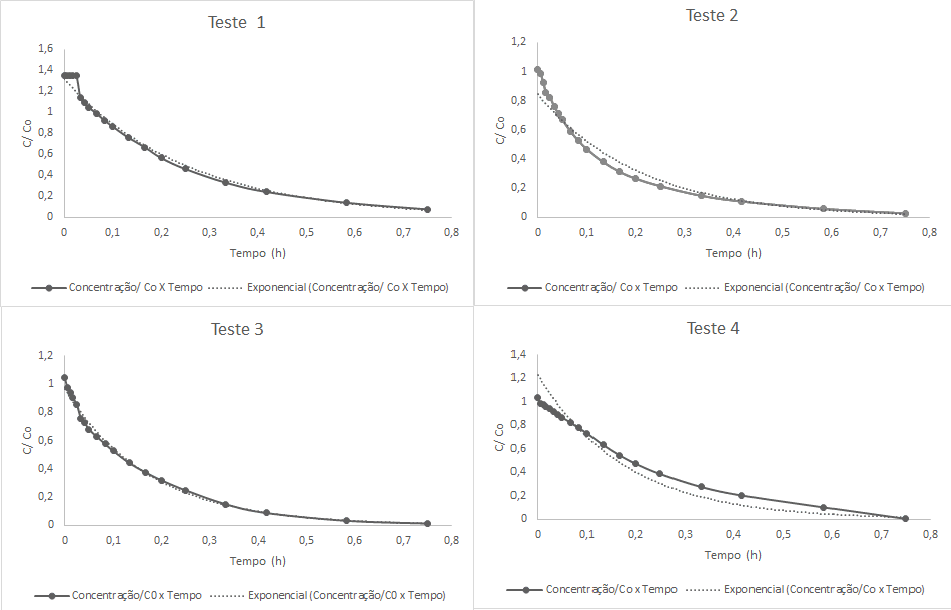
A introdução de uma perturbação em degrau negativo corresponde a um processo de diluição gradativa ao longo do tempo. Inicialmente, o marcador se encontra dentro do reator e possuí uma concentração C0 conhecida. A concentração de marcador à saída do sistema, Cs(t), é medida ao longo do tempo para determinar a função E(t). Na quantificação do estímulo utilizado para verificar a variação da concentração ao longo do tempo, projetaram-se os gráficos da concentração final/concentração inicial em relação ao tempo, que podem ser observados a seguir:
Figura 11 – Gráficos do estímulo degrau para cada teste realizado.
3.7 DETERMINAÇÃO DA FRAÇÃO DA CORRENTE
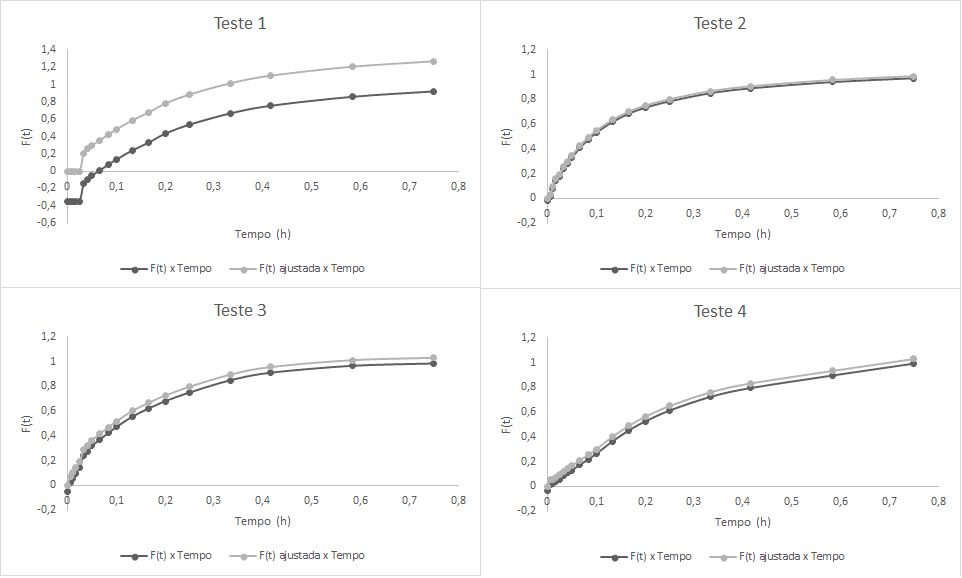
Para determinar a fração da corrente ao longo do tempo, projetaram-se os gráficos F(t) x T, através da Equação de Fração de Corrente (FOGLER, 2012).
Onde, F = Fração de corrente; C = Concentração atual da solução de traçador (g.L-1); C0= Concentração inicial da solução de traçador (g.L-1).
Na análise dos dados obtidos, verificou-se que em todos os testes, a concentração final das soluções de traçador se apresentou maior que a concentração inicial, o que promoveu pequenos desvios do esperado. Novamente, ajustaram-se as curvas conforme pode ser verificado na Figura 12. O teste 2 foi o que apresentou menor desvio.
Figura 12 – Gráficos da Função F(t) x Tempo.
3.8 TEMPO DE RESIDÊNCIA
Para quantificar o tempo de residência foi utilizada a Equação da Função E (FOGLER, 2012).
Onde: (- C/ C0)1 = Concentração final de traçador/ Concentração inicial de traçador na análise do tempo 1; (- C/ C0)2 = Concentração final de traçador/ Concentração inicial de traçador na análise do tempo 2; T2 = Tempo 2 (h); T1 = Tempo 1 (h).
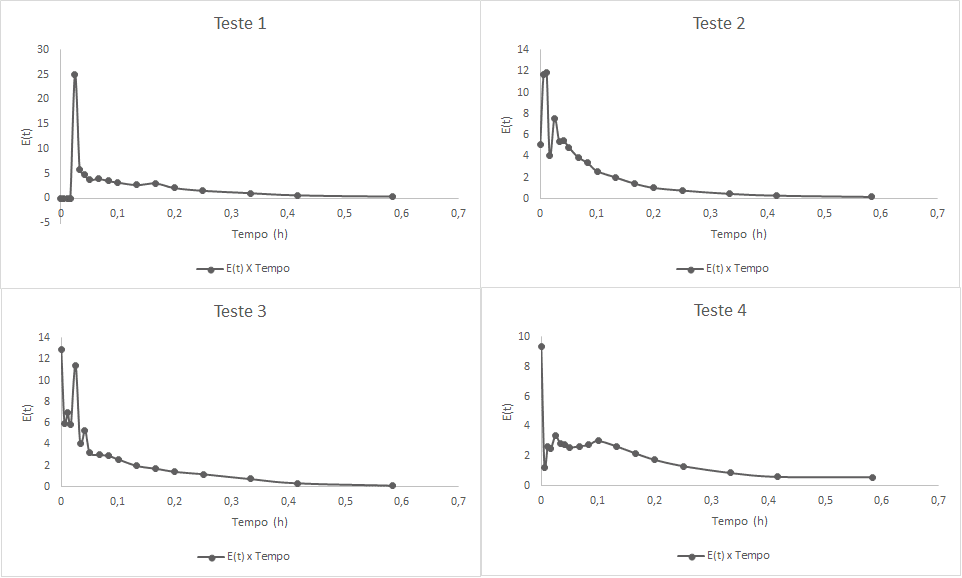
Após a aplicação da Equação 5, construíram-se os gráficos de E(t) x Tempo, para cada teste, conforme está descrito na Figura 13. Através destes, analisou-se o comportamento do escoamento no reator, onde, com o auxílio da Figura 2, compararam-se os resultados obtidos com o teórico. Assim, foi possível constatar que os desvios ocorreram, de forma geral, no início do processo, uma vez que, levou-se um tempo para se alcançar a estabilidade do sistema. Neste período transiente, as partículas ainda não estavam misturadas homogeneamente, demonstrando assim, a não idealidade do reator, através da formação de caminhos preferencias. O teste 2 foi o que mais se aproximou do ideal.
Figura 13 – Gráficos da Função E(t) x Tempo.
3.9 DETERMINAÇÃO DO TEMPO MÉDIO DE RESIDÊNCIA
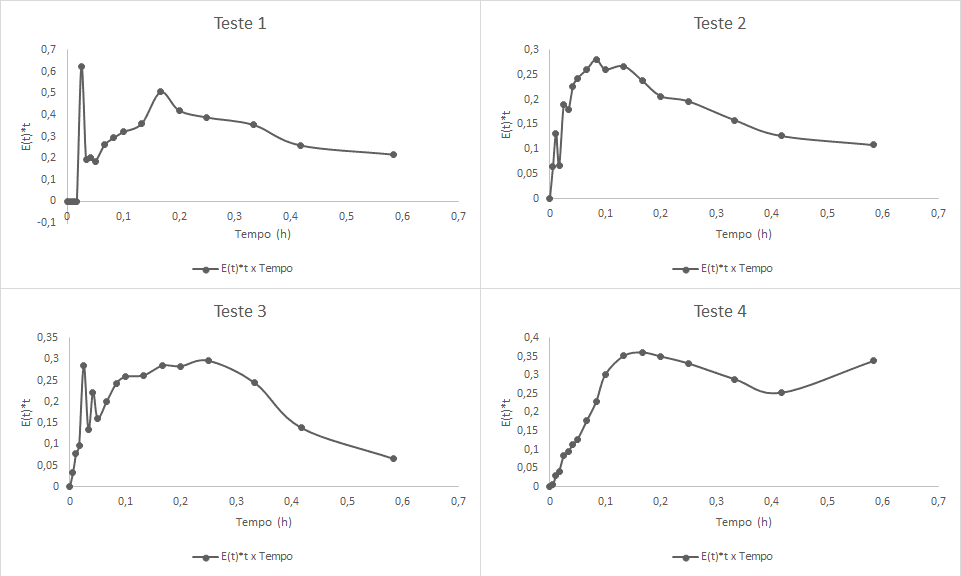
Para determinar o tempo de residência médio, de forma experimental, multiplicou-se o tempo pela função E(t) para cada amostra, conforme está descrito na Equação 6 (SCHMAL, 2013). Os gráficos construídos podem ser verificados através da Figura 14.
A partir da área do gráfico ou da somatória de todos os pontos, foi possível determinar o tempo médio de residência para cada teste, onde, os valores obtidos podem ser observados a seguir: teste 1 = 4,59 h, teste 2 = 3,21h, teste 3 = 3,29 h e teste 4 = 3,48 h. Estes valores serão comparados com o tempo espacial.
Figura 14 – Gráficos da Função E(t)*t x Tempo.
3.10 DETERMINAÇÃO DO TEMPO ESPACIAL
Para determinar o tempo espacial do reator foi usada a função para determinar o tempo médio de residência (SCHMAL, 2013).
Onde, τ = tempo espacial, V = volume do reator e vo = vazão do reator.
Após aplicar os valores do volume e da vazão na fórmula da Equação 7, determinou-se o tempo espacial para cada teste, conforme apresentados na Tabela 10.
Tabela 10 – Valores do tempo espacial obtidos para cada teste conforme os respectivos valores de volume e vazão indicados.
| Volume (V) (mL) | Vazão (vo) (mL.h-1) | τ (h) |
| 1850 | 7200 | 0,2569444 |
| 0925 | 7200 | 0,1284722 |
| 0925 | 7200 | 0,1284722 |
| 1850 | 7200 | 0,2569444 |
Fonte: Própria autor.
A partir dos valores do tempo espacial obtido, comparou-se com os valores do tempo médio de residência para verificar a idealidade do reator. Quanto maior a diferença entre eles, maior a não idealidade do reator.
Tabela 11 – Valores do tempo médio de residência e do tempo espacial.
| Testes | Tempo de Residência Médio (h) | τ (h) |
| 1 | 4,59 | 0,2569444 |
| 2 | 3,21 | 0,1284722 |
| 3 | 3,29 | 0,1284722 |
| 4 | 3,48 | 0,2569444 |
FONTE: Próprio autor.
Assim, segundo a Tabela 11, como o tempo espacial diferiu do tempo médio de residência, verificou-se que o reator tanque contínuo não se comporta como um CSTR e ainda, que o teste 2 foi o que menos apresentou desvio.
4. CONCLUSÕES
Com a realização do projeto de reator de tanque contínuo em questão, foi possível levantar diversos pontos que são fundamentais para a execução do protótipo. Primeiramente, o estudo e o desenvolvimento do reator foram essenciais para dimensionar a importância que o Engenheiro Químico tem dentro da indústria. Pois, é através de projetos de processos químicos que se avaliam a eficiência, rendimento e custo necessários para produzir um produto. Ainda, vale ressaltar que o objetivo deste trabalho foi analisar o volume e o agitador do reator para verificar a forma que estes interferem no funcionamento do reator.
Portanto, segundo o estudo da DTR, concluiu-se que a velocidade de agitação do processo deve ser proporcional ao volume do reator, ou seja, quanto maior o volume, mais intensa deve ser a agitação. Constatou-se também, que a conversão do produto está relacionada ao tempo em que as partículas ficam dentro do reator, desta forma, para se obter uma saída específica, deve-se determinar o volume mais adequado para o processo. Já em relação ao estudo dos agitadores, observou-se que embora o agitador com mais pás fosse o mais indicado à proporcionar uma mistura mais homogênea, em sistemas com volumes menores, por se encontrarem menos submersos em solução, o peso dos agitadores interferem no processo, o que dificulta a homogenização da reação, além de favorecer a formação de vórtices.
Portanto, o baixo rendimento experimental foi devido à não idealidade do reator. Conforme resultados obtidos, todos os testes apresentaram desvios. Estes desvios geraram uma diferença entre a conversão teórica e a experimental de aproximadamente 3,8 vezes, o que demonstra que alguns desafios ainda precisam ser superados através de um controlador de vazões mais preciso e de artefatos como chicanas para alcançar a idealidade do reator tipo tanque contínuo.
5. REFERÊNCIAS
FOGLER, H. S. Elementos de engenharias das reações químicas. 4. Ed. Rio de Janeiro: LTC, 2012.
LEVENSPIEL, O. Engenharia das reações químicas. São Paulo: Edgard Blücher Ltda., 2000.
Nonlinear Model Library. Disponível em: <www.Hedengren.net/research/models. htm>. Acesso em: 23/04/2017.
Oxirredução do Permanganato de Potássio e Água Oxigenada. Disponível em: <https://www.youtube.com/watch?v=Qw3qWLS6cUg>. Acesso em: 23/04/2017.
SASSAKI, R. A. Distribuição de tempos de residência em sistemas alimentados com vazão variável. 2005. Tese (Mestrado em Ciências em Engenharia Civil, Programa De Pós-Graduação Em Engenharia Civil) – Universidade Federal do Rio de Janeiro, COPPE. Disponível em: <http://wwwp.coc.ufrj.br/teses/mestrado/rh/2005/Teses/SASSAKI_RA _05_t_M_rhs.pdf>. Acesso em: 09/04/2017.
SCHMAL, M. Cinética e reatores: aplicação na engenharia química. 2. Ed. Rio de Janeiro: Synergia: COPPE/UFRJ: FAPERJ, 2013.
SCHULTZ, G.: LAUER, J.: LOPES, J. M.: RANGEL, R. S. Modelagem e simulação dos reatores químicos BR e PFR no EMSO e GNU OCTAVE. 2014. Artigo (Trabalho de Graduação em Engenharia Química) – Departamento de Engenharia Química, Faculdade Integradas de Aracruz, Espírito Santo, 2014.
STEPHANOPOULOS, G. Chemical process control: na introduction to theory and practice. New Jersey: Prentice Hall, 1984.
[1] Engenheira Química pela Universidade São Francisco.
[2] Engenheiro Químico pela Universidade São Francisco.
[3] Professora na Universidade São Francisco (USF); Pós-doutorado em Ciências Atmosféricas pelo IAG/USP; Doutora em Materiais pelo IPEN/USP; Mestre em Materiais pelo IPEN/USP, Engenheira Química pela UFSCar.
Enviado: Setembro, 2019.
Aprovado: Outubro, 2019.