ARTIGO ORIGINAL
GOMES, Alexandre Merison Santos [1], SOUZA, Rafael Araujo [2]
GOMES, Alexandre Merison Santos; SOUZA, Rafael Araujo de. O Princípio da Inclusão – Exclusão e as Permutações Caóticas: Métodos Alternativos de Contagem. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 08, Vol. 16, pp. 193-209, Agosto de 2018. ISSN:2448-0959
RESUMO
Pretende‐se neste artigo abordar aspectos teóricos que norteiam o princípio da Inclusão-Exclusão e as Permutações Caóticas, além de apresentar formas de como aplicar tais conhecimentos. Refletindo sobre necessidade humana de contar e quantificar os elementos de um determinado conjunto, garantindo a continuidade de algumas ações e a uma reavaliação e redirecionamento de outras. Este texto está dividido em três partes: na primeira é apresentado alguns aspectos conceituais relativos sobre o Princípio da Inclusão-Exclusão. Na segunda, tem‐se um detalhamento sobre as Permutações Caóticas, com sua dinâmica e seus resultados e, na terceira, é abordado a aplicação do Princípio da Inclusão-Exclusão nas Olimpíadas Brasileiras de Matemática das Escolas Públicas (OBMEP).
Palavras-Chave: Inclusão-Exclusão, Permutações, Caóticas, Obmep.
1. INTRODUÇÃO
Os métodos de contagem ultimamente não têm sido muito bem tratados na educação básica e nem no ensino superior, além dos livros didáticos também não se aprofundarem mais sobre o assunto, que é frequente no ENEM, OBMEP e até mesmo em concursos públicos.
Uma pergunta que surge é: Por quê? Muito provável que pelo fato do assunto exigir um pouco mais de atenção, de raciocínio cauteloso, visto que se deve analisar caso a caso e isso para o aluno da educação básica não é prazeroso, sem falar que muitos professores demonstram grandes dificuldades ou falta de interesse quando se fala de combinatória.
Uma vantagem do ensino dos métodos de contagem é o fato da possibilidade de saber a quantidade de elementos de um determinado conjunto sem haver a necessidade de enumerá-los. Como por exemplo, se um aluno tivesse que saber quantos números de três algarismos todos distintos existem? Uma possibilidade seria enumerá-los e contar, no entanto não seria um trabalho rápido e prazeroso. Portanto, se utilizasse os métodos de contagem, no caso, o princípio multiplicativo, chegaria a resposta de forma rápida e clara, no caso, números.
Além do Princípio multiplicativo, a combinatória possui diversas ferramentas, como as permutações, arranjos, combinações e outros métodos alternativos, onde nesse trabalho será tratado de dois deles, no caso o Princípio da Inclusão – Exclusão e as Permutações Caóticas.
Frente a este contexto, o presente trabalho tem como intuito trazer à tona a importância do Princípio da Inclusão – Exclusão para o desenvolvimento da matemática discreta, analisando os principais resultados e teoremas associados a contagem e examinando aplicações importantes, como as Permutações caóticas, sem falar que tais estudos podem se estender para estudos probabilísticos.
Com o propósito descrito acima, este trabalho foi organizado da seguinte maneira. A segunda seção é feita a apresentação do Princípio da Inclusão – Exclusão, em sua forma mais simples e no decorrer da seção fazendo suas generalizações, até chegar à sua forma geral, sempre com exemplos de aplicações.
Na terceira seção versa sobre as Permutações Caóticas, onde se usa o Princípio da Inclusão – Exclusão para a sua demonstração e segue com algumas aplicações.
Na quarta seção, são apresentados alguns problemas das Olimpíadas Brasileiras de Matemática das Escolas Públicas (OBMEP), confirmando a importância e aplicabilidade do Princípio da Inclusão – Exclusão.
2. METODOLOGIA
2.1 TIPO DE PESQUISA
A descrição das etapas deste estudo tem como finalidade facilitar a compreensão sobre o processo e a lógica de construção da pesquisa e, no sentido de mostrar, o percurso trilhado e as técnicas de pesquisas empregadas para o cumprimento dos objetivos.
Portanto, a pesquisa apresenta – se como bibliográfica, pois a mesma apresenta um levantamento bibliográfico do material já publicado sobre o assunto; Nessa fase inclui-se também a pesquisa pura, com o objetivo de satisfazer uma necessidade pelo conhecimento;
Quanto aos objetivos apresenta – se como exploratória com abordagem metodológica, classificando-se como qualitativa em função da análise da teoria ser feita apenas a partir da discussão dos autores teóricos. Nesse sentido, tem o objetivo de mostrar a importância do Princípio da Inclusão – Exclusão para o desenvolvimento da matemática discreta, analisando os principais resultados e teoremas associados a contagem e examinando aplicações importantes, como as Permutações caóticas, e assim, tais estudos podem se estender para estudos probabilísticos.
2.2 PROCEDIMENTO
No primeiro momento será feita a escolha da temática, em seguida haverá o levantamento do material bibliográfico para a construção do artigo. Após a análise do material, o estudo desenvolvido apresenta – se da seguinte forma: Será iniciado com o caso mais simples do princípio da Inclusão – Exclusão fazendo as extensões à medida que o trabalho é desenvolvido para em seguida apresentar uma das principais aplicações, no caso, as Permutações Caótica, findando com alguns problemas olímpicos.
3. O PRINCÍPIO DA INCLUSÃO – EXCLUSÃO
O Princípio da Inclusão – Exclusão é um modelo que serve para contar a quantidade de elementos que pertencem a uma união qualquer de conjuntos não necessariamente disjuntos. A saber, o número de elementos de um conjunto qualquer será representado por . Sendo assim, os resultados aqui discutidos estão relacionados com as obras [1], [2] e [3].
Definição 3.1: Dados dois conjuntos e finitos que não possuem elementos comuns, o número de elementos da união é exatamente a soma do número de elementos de cada conjunto, ou seja, se e são disjuntos, então:
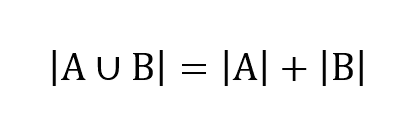 Este princípio, apesar de simples, pode ser uma ferramenta importante na resolução de muitos problemas. Vejamos o problema a seguir:
Este princípio, apesar de simples, pode ser uma ferramenta importante na resolução de muitos problemas. Vejamos o problema a seguir:
Problema 3.1: Quantos são os números naturais que se escrevem com três algarismos distintos?
Solução: Note que não será possível resolver esse problema de forma direta utilizando o princípio multiplicativo, pois para um número ser par ele deve terminar em ou . Com isso, a primeira decisão a ser tomada deve ser aquela com mais restrições, no caso, o número que vai ocupar a posição das unidades, que pode ser tomada de cinco maneiras, seguindo para a posição das centenas, que pode ser tomada de quantas maneiras? A melhor reposta é: Depende.![]()
Pois, se o zero está na unidade, então se tem possibilidades para a centena, por outro lado, se a unidade não for o zero, tem-se possiblidades para a centena. Sendo assim, para resolver o problema, defina os conjuntos disjuntos a seguir:
![]() Conjunto dos números pares com algarismos distintos que terminam com 0.
Conjunto dos números pares com algarismos distintos que terminam com 0.
Conjunto dos números pares com algarismos distintos que não terminam com 0.
Sendo assim, tem-se: ![]() Portanto,
Portanto,
![]() números pares com algarismos distintos.
números pares com algarismos distintos.
Veja que o principio apresentado, proporcionou a resolução do problema de maneira simples e rápida. A seguir tem-se uma extensão desse principio:
Princípio da Inclusão-Exclusão: Dados os conjuntos finitos ![]() dois a dois disjuntos
dois a dois disjuntos ![]()
Problema 3.2: Uma reunião havia certo número de pessoas e todos os presentes apertaram as mãos entre si. Sabendo que ao todos foram feitos cumprimentos, calcule o número de pessoas presentes à reunião.
Solução: Para resolver o problema, enumere as pessoas com os números do conjunto ![]() . Cada aperto de mão associe um par
. Cada aperto de mão associe um par ![]() significando que a pessoa i apertou a mão da pessoa j. Sendo assim, os apertos de mão envolvendo a pessoa 1 foi:
significando que a pessoa i apertou a mão da pessoa j. Sendo assim, os apertos de mão envolvendo a pessoa 1 foi:
De modo análogo, os apertos de mão envolvendo a pessoa 2 que não envolva a pessoa 1 é:
É importante destacar que os apertos (1,2) e (2,1) é o mesmo aperto. Dessa maneira, pode-se definir, de um modo geral:
Observe que para , e que todos os apertos aparecem em um dos . Sendo assim, contém todos os apertos de mão. Logo, pelo principio da inclusão-exclusão:
que resolvendo a equação em ![]() , obtém-se
, obtém-se ![]() =12.
=12.
A seguir, será discutida outra extensão do principio, no caso em questão, os conjuntos agora não são necessariamente disjuntos.
Proposição 3.1: Sejam e dois conjuntos finitos quaisquer. Então,
Demonstração: Note que, ![]() , com
, com ![]() e
e ![]() conjuntos disjuntos. Aplicando o princípio da inclusão-exclusão, tem-se:
conjuntos disjuntos. Aplicando o princípio da inclusão-exclusão, tem-se: ![]()
![]() que será chamado de (i) . Observe ainda que,
que será chamado de (i) . Observe ainda que, ![]() , com e disjuntos. Aplicando o principio da inclusão – exclusão novamente, obtém-se:
, com e disjuntos. Aplicando o principio da inclusão – exclusão novamente, obtém-se: ![]() , que será chamado de (ii). Dessa maneira, substituindo (ii) em (i), tem-se que:
, que será chamado de (ii). Dessa maneira, substituindo (ii) em (i), tem-se que:
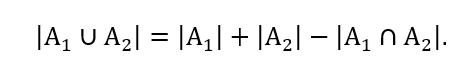
Como se queria demonstrar.
Problema 3.3: Quantos inteiros entre e são divisíveis por ou ?
Solução: Para resolver esse problema, defina os conjuntos:
![]() Conjunto dos inteiros entre 1 e 1000 que são divisíveis por 3;
Conjunto dos inteiros entre 1 e 1000 que são divisíveis por 3;
![]() Conjuntos dos inteiros entre 1 e 1000 que são divisíveis por 7;
Conjuntos dos inteiros entre 1 e 1000 que são divisíveis por 7;
O objetivo agora é calcular o número de elementos de (A ∪ B) . Com isso,
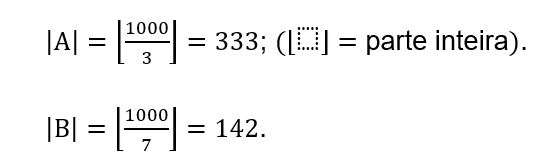
Além disso, deve-se determinar quantos elementos são comuns a A e B, ou seja, (A ∩ B) , no caso:
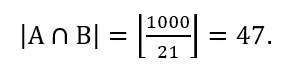
Segundo a Proposição 2.1, tem-se:
![]()
No corolário a seguir, está definido o Principio da Inclusão – Exclusão a três conjuntos não necessariamente disjuntos.
Corolário 3.1: Sejam ![]() e três conjuntos finitos quaisquer. Então,
e três conjuntos finitos quaisquer. Então,
![]()
Demonstração: Pela Proposição 2.1, tem-se:
![]() Aplicando novamente a Proposição 2.1 tem-se:
Aplicando novamente a Proposição 2.1 tem-se:
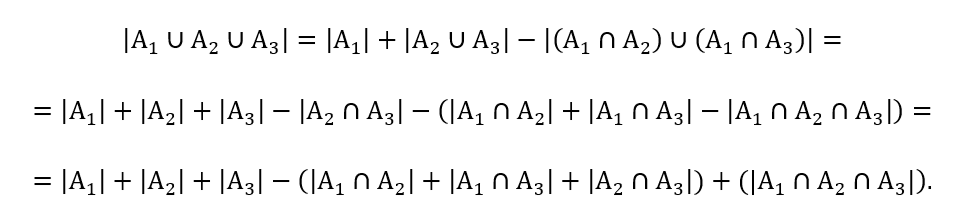
A seguir, será apresentada a visão mais geral do Princípio da Inclusão – Exclusão.
Teorema 3.1 (Princípio da Inclusão-Exclusão / Visão Geral): Seja Ω um conjunto, ![]() subconjuntos de Ω e
subconjuntos de Ω e

Observe que há ![]() parcela em
parcela em ![]() , parcelas em
, parcelas em ![]() , e assim por diante. Dessa maneira:
, e assim por diante. Dessa maneira:
(a) O número de elementos de que pertencem a exatamente dos conjuntos ![]()
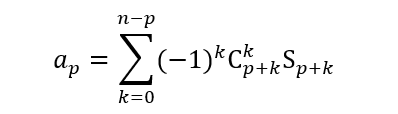 (b) O número de elementos de Ω que pertencem a pelo menos
(b) O número de elementos de Ω que pertencem a pelo menos ![]() dos conjuntos
dos conjuntos ![]()
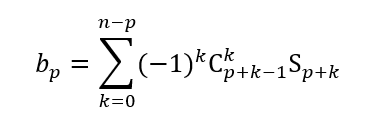 (c) O número de elementos do conjunto
(c) O número de elementos do conjunto ![]() é
é
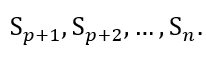
Vale salientar que a parte (a), no caso , é devida ao algebrista inglês J. J. Sylvester (1814-1897), onde é conhecida pelo nome de fórmula do Crivo. Já no caso geral, é devida ao matemático francês Camille Jordan (1858-1922). Já parte (c) é devida ao matemático português, professor da Escola Naval de Portugal, Daniel Augusto da Silva (1814-1878).
Demonstração:
Caso (a). É perceptível que, se um determinado elemento de Ω pertence a menos do que ρ dos conjuntos ![]() , ele não será contado na soma
, ele não será contado na soma ![]() , logo o que deve-se provar é que se um determinado elemento de Ω pertence a exatamente ρ dos conjuntos, então ele é contado uma vez na soma de
, logo o que deve-se provar é que se um determinado elemento de Ω pertence a exatamente ρ dos conjuntos, então ele é contado uma vez na soma de ![]() e que se pertence a mais do que ρ conjuntos de
e que se pertence a mais do que ρ conjuntos de ![]() então não será contado na soma
então não será contado na soma ![]() . Nisto, a soma é:
. Nisto, a soma é:
![]() Um elemento de Ω que está em exatamente ρ dos conjuntos
Um elemento de Ω que está em exatamente ρ dos conjuntos ![]() é contado uma vez apenas em
é contado uma vez apenas em ![]() e não é contado em
e não é contado em ![]() . Logo, ele é contado
. Logo, ele é contado ![]() vez.
vez.
Um elemento de Ω que pertence a exatamente ![]() dos conjuntos
dos conjuntos ![]() é contado em
é contado em 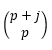 das parcelas de
das parcelas de ![]() , em
, em ![]() das parcelas de
das parcelas de ![]() em
em ![]() das parcelas de , e assim por diante. Daí, o número de vezes que ele é contado na soma de
das parcelas de , e assim por diante. Daí, o número de vezes que ele é contado na soma de ![]() é
é
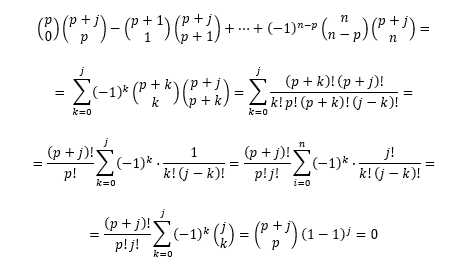
Caso (b). Tem-se que
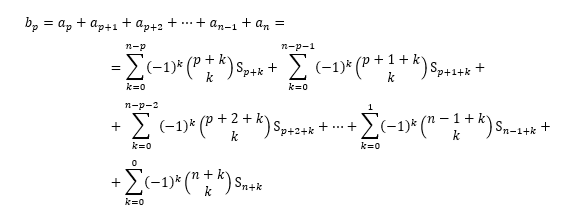
Observe que o coeficiente de no ![]() membro é
membro é
Logo,
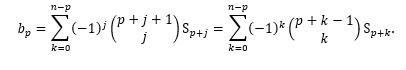
Caso (c). Tem-se que:
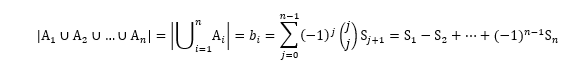
Vale ressaltar que de forma análoga, pode-se mostrar a versão probabilística do princípio da inclusão-exclusão. Veja alguns problemas no qual se aplica o princípio acima demonstrado.
Problema 3.4: No colégio Fantástico, foram entrevistados 78 estudantes. Destes, 32 estavam fazendo um curso de francês; 40 um curso de física; 30 um curso de matemática; 23 um curso de história; 19 francês e física; 13 francês e matemática; 15 física e matemática; 2 francês e história; 15 física e história; 14 matemática e história; 8 francês, física e matemática; 8 francês, física e história; 2 francês, matemática e história; 6 física, matemática e história e 2 estavam fazendo todos os quatro cursos. Quanto estudantes estavam fazendo pelo menos 1 curso nas 4 áreas mencionadas?
Solução: Sejam ![]() e os conjuntos dos estudantes que fazem francês, física, matemática e história, respectivamente.
e os conjuntos dos estudantes que fazem francês, física, matemática e história, respectivamente.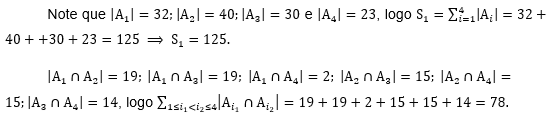

Uma aplicação do Princípio da Inclusão – Exclusão é na teoria dos números com relação à função , chamada de função de Euler, onde é definido para cada inteiro como sendo o número de inteiros positivos que são primos com e não superiores a . Por exemplo, , pois os inteiros positivos que não superam e são primos com são e. Veja a seguir:
– Problema 2.5: Mostre que se a decomposição de em fatores primos é n = ![]() primos distintos, então
primos distintos, então
![]()
Demonstração: Defina os conjuntos abaixo
Ω= Conjunto dos inteiros positivos menores ou iguais a.
![]() = Conjunto dos elementos de que são múltiplos de.
= Conjunto dos elementos de que são múltiplos de.
Note que é preciso determinar o número de elementos Ω de que são primos com n, ou seja, o número de elementos que não pertence a nenhum dos conjuntos ![]() . Observe que
. Observe que ![]() é o número de elementos de Ω que pertence a exatamente nenhum, ou seja, zero dos conjuntos
é o número de elementos de Ω que pertence a exatamente nenhum, ou seja, zero dos conjuntos ![]() .
.
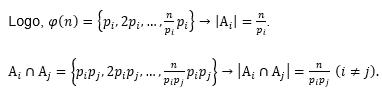
E assim sucessivamente. Tem-se então:
![]()
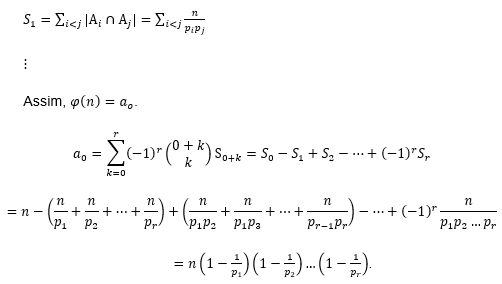
4. PERMUTAÇÕES CAÓTICAS
Uma das principais aplicações do Princípio da Inclusão – Exclusão é a permutação caótica, como será abordado a seguir. Os resultados desta seção estão relacionadas as referencias [1] e [3].
Definição 4.1: Uma permutação dos números (1,2,3,…n) é dita caótica (ou desordenadamente) quando nenhum elemento está no seu lugar primitivo.
Observe que a permutação 4321 de 1234 é uma permutação caótica, no entanto 3241 não é, pois o 2 permanece em sua posição primitiva.
Vale salientar que as permutações caóticas valem para qualquer conjunto de objetos, não necessariamente numéricos. São utilizados conjuntos numéricos apenas para efeito de demonstração.
Teorema 4.1 (Permutações Caóticas): Para n > 1 há precisamente
![]()
Permutações caóticas de ![]()
Demonstração: Considere o conjunto Ω = { 1,2,3,…, n } e defina ![]() , = Conjunto das permutações de (1,2,3,…,n) em que o número i ocupa o i – ésimo lugar, i ∈ {1,2,3,…, n}.
, = Conjunto das permutações de (1,2,3,…,n) em que o número i ocupa o i – ésimo lugar, i ∈ {1,2,3,…, n}.
Assim, o objetivo é determinar o número de elementos do conjunto Ω das permutações de (1,2,3,… n) que pertencem a exatamente zero dos conjuntos ![]() . Dessa maneira, tem-se:
. Dessa maneira, tem-se:
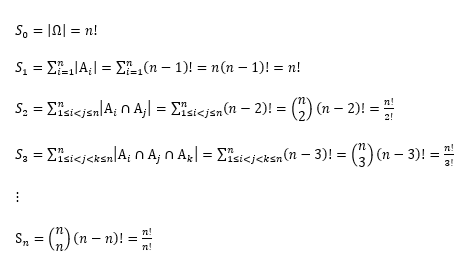
Portanto, o número de elementos de que estão em exatamente zero dos conjuntos ![]() é
é
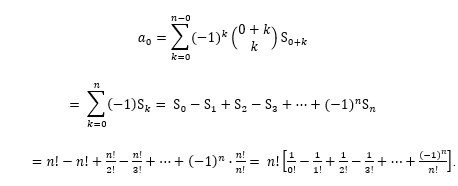
Logo, o número de permutações caóticas de (1,2,3,…, n) é
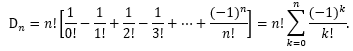
Observação 4.1: É possível mostrar que ![]() é aproximadamente igual a
é aproximadamente igual a ![]() ou seja,
ou seja, ![]() é o número inteiro mais próximo de
é o número inteiro mais próximo de ![]()
Veja o problema a seguir:
Problema 4.1: Uma recepcionista recebeu chapéus, mas estes ficaram totalmente misturados. Decidiu então, devolvê-los aos mesmos. Calcular a probabilidade de que nenhum homem receba o seu.
Solução: Vale lembrar que a probabilidade é definida pela razão entre os casos favoráveis com os possíveis, sendo assim, tem-se:
O número de casos favoráveis consiste no número de permutações caóticas de n objetos (chapéus), pois nenhum dos homens deve ficar com o seu chapéu. Já o número de casos possíveis, consiste em n!(o número de permutações simples dos n chapéus), logo, a probabilidade é:
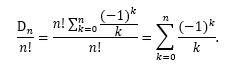
Note que esta probabilidade se estabiliza rapidamente quando n → ∞, ou seja,
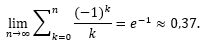
5. O PRINCÍPIO DA INCLUSÃO – EXCLUSÃO NA OBMEP
Nesta seção serão apresentados alguns problemas da OBMEP na qual será utilizada como “ferramenta” para resolução de tais problemas o Princípio da Inclusão – Exclusão. Os resultados aqui discutidos estão associados com a referência [4].
Problema 5.1 (OBMEP – 2016): No refeitório da escola Quixajuba, na hora do almoço, 130 alunos comeram carne e 150 comeram macarrão, sendo que ![]() dos alunos comeram carne e também macarrão. Além disso, 70 alunos não comeram carne nem macarrão. Quantos alunos comeram carne, mas não comeram macarrão?
dos alunos comeram carne e também macarrão. Além disso, 70 alunos não comeram carne nem macarrão. Quantos alunos comeram carne, mas não comeram macarrão?
Solução: Seja x o número de alunos na escola. E defina os conjuntos:
![]() = Conjunto dos alunos que comem carne
= Conjunto dos alunos que comem carne
![]() = Conjunto dos alunos que comem macarrão
= Conjunto dos alunos que comem macarrão
Sabe-se que ![]() e e, além disso, os que comem carne e macarrão são
e e, além disso, os que comem carne e macarrão são ![]() , ou seja,
, ou seja, ![]() Com isso, temos:
Com isso, temos:
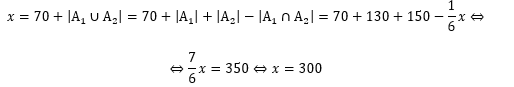
Logo, o número de alunos que comem apenas carne é ![]() 80 alunos.
80 alunos.
Problema 5.2 (OBMEP – 2014): Em uma orquestra de cordas, sopro e percussão, 23 pessoas tocam instrumentos de corda, 18 tocam instrumentos de sopro e 12 tocam instrumentos de percussão. Nenhum de seus componentes toca os três tipos de instrumentos, mas 10 tocam instrumentos de corda e sopro, 6 tocam instrumentos de corda e percussão e alguns tocam instrumentos de sopro e percussão. No mínimo, quantos componentes há nessa orquestra?
Solução: Defina os conjuntos:
![]() = Conjunto das pessoas que tocam instrumentos de corda
= Conjunto das pessoas que tocam instrumentos de corda
![]() = Conjunto das pessoas que tocam instrumentos de sopro
= Conjunto das pessoas que tocam instrumentos de sopro
![]() = Conjunto das pessoas que tocam instrumentos de percussão
= Conjunto das pessoas que tocam instrumentos de percussão
Com isso tem-se:

Logo o número de componentes da orquestra é:
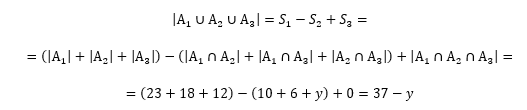
Observe que ![]() com isso resta apenas 8 pessoas em
com isso resta apenas 8 pessoas em ![]() e 6 pessoas em
e 6 pessoas em ![]() , caso contrário teria –se
, caso contrário teria –se ![]() . Logo,
. Logo, ![]() é mínimo quando y é máximo, ou seja,
é mínimo quando y é máximo, ou seja, ![]() pessoas.
pessoas.
CONSIDERAÇÕES FINAIS
Os métodos de contagem proporcionam uma destreza ao quantificar os elementos de um determinado conjunto, sem precisar enumera-los, sem falar que é Pré-requisito para o estudo de Probabilidade, que está presente, tanto na educação básica, como em muitos programas de cursos em nível superior, além de está frequentemente em concursos públicos e olimpíadas.
Com este trabalho acredita-se que foi possível mostrar a importância do princípio da Inclusão-Exclusão para o desenvolvimento da matemática discreta, além de ser uma ferramenta útil na resolução de problemas olímpicos.
Existem ainda outros métodos de contagem que podem ser bem explorados, com as permutações circulares e caóticas, aqui abordada como consequência do Princípio da Inclusão-Exclusão, o princípio da Reflexão e os Lemas de Kaplansky, além das contagens duplas. Com isso, o trabalho em questão é apenas uma porta de entrada para o estudo dos métodos alternativos de contagem.
REFERENCIAS
[1] MORGADO, A.C. et.al. Análise Combinatória e Probabilidade. 9ªed. Rio de Janeiro: SBM, 1991.
[2] OLIVEIRA, K.I.M.; FERNÁNDEZ, A.J.C. Iniciação à Matemática: Um Curso com Problemas e Soluções. 2ªed. Rio de Janeiro: SBM, 2012.
[3] NETO, A.C.M. Tópicos de Matemática Elementar: Combinatória. vol.4. 2ªed. Rio de Janeiro:SBM, 2016.
[4] BRASIL. Olimpíada Brasileira de Matemática. OBMEP 2017. Rio de Janeiro, 2017. Disponível em: <http:// www.obmep.org.br/provas.htm>. Acessado em: 06 set. 2017.
[1] Professor Especialista em Metodologia do Ensino da Matemática.
[2] Professor Especialista em Metodologia do Ensino da Matemática.

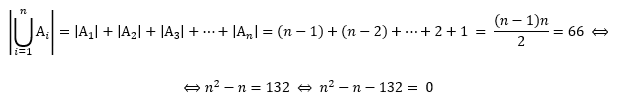
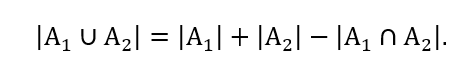

Uma resposta
Excelente artigo!Ele me ajudou a entender problemas mais complexos de métodos de contagem!!! Como, por exemplo, o problema do amigo oculto!