Contribuições do Microsoft Office Excel ao ensino da Estatística

ARTIGO ORIGINAL

FRANCISCO, Isabelly Maria Mendes Barbosa ^[1], OLIVEIRA, Iran Rodrigues de ^[2], SILVA, José Vieira da ^[3]

FRANCISCO, Isabelly Maria Mendes Barbosa. OLIVEIRA, Iran Rodrigues de. SILVA, José Vieira da. Contribuições do Microsoft Office Excel ao ensino da Estatística. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 01, Vol. 10, pp. 131-147. Janeiro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/contribuicoes-do-microsoft

RESUMO

O presente artigo, pesquisa bibliográfica, relata as contribuições do software de planilha eletrônica, Microsoft Office Excel, ao ensino da estatística. Tendo em vista familiaridade dos alunos com as novas tecnologias, introduzi-las ao ensino da estatística dinamiza a aula, tornando assim, o aprendizado proveitoso. Os objetivos propostos pelos Parâmetros Curriculares Nacionais, Orientações Curriculares para o Ensino Médio e a Base Nacional Comum Curricular, recomendam o uso de planilhas eletrônicas no ensino da matemática. Dessa forma, enfatiza-se o uso do Microsoft Office Excel, como ferramenta pedagógica, contribui para o entendimento das aplicações da estatística, por possuir interface amigável e de fácil utilização. Através do software, demonstrou-se o uso de algumas ferramentas que auxiliam no processo de ensino-aprendizagem, partindo desde a efetuação de simples cálculos de média, mediana e moda à construção de tabelas de frequência e de gráficos. Com a utilização correta dos recursos apresentados, torna-se viável direcionar a atenção do aluno à realização de melhores análises em suas pesquisas, haja vista, a administração do tempo em cálculos repetitivos. A fim de que isto se torne uma realidade, faz-se necessária formação e/ou capacitação dos professore, visando o esclarecimento de eventuais dúvidas por parte dos alunos, permitindo-lhes, dessa forma, um bom uso da ferramenta.

Palavras-chave: Estatística, planilha eletrônica, ensino.

INTRODUÇÃO

O uso da tecnologia e suas formas de interação está presente na vida das atuais gerações, através do uso de diversos aplicativos (de mensagens, redes sociais e de serviços). Dessa forma, o aluno envolve-se com a tecnologia, dentro e fora do ambiente escolar. A inserção das mídias digitais e softwares, como ferramentas pedagógicas, podem ser um meio eficaz de dinamizar as aulas, tornando-as também, atraentes e inovadoras.

A tecnologia de informação e comunicação está revolucionando o dia a dia da sociedade atual. A mesma tecnologia que exige a capacitação de seu usuário para fazer um bom uso de suas ferramentas, possui também recursos que auxiliam no processo de aprendizagem da Matemática e consequentemente da Estatística. As Orientações Curriculares para o Ensino Médio, Ciências da Natureza, Matemática e suas Tecnologias diz: “É contemplar uma formação escolar nesses dois sentidos, ou seja, a Matemática como ferramenta para entender a tecnologia, e a tecnologia como ferramenta para entender a Matemática.”¹

Com o intuito de obter maior aproveitamento no ensino da Matemática, é necessária a aplicação das novas tecnologias em sala de aula, como ferramentas para o desenvolvimento e efetivação do processo de ensino-aprendizagem. Esta ação promove, por parte do aluno, significativo avanço de sua aprendizagem, permitindo-lhe, assim, experimentar o contato com as tecnologias, criando, por conseguinte, o hábito de utilização destas ferramentas com autonomia e senso de investigação. Com base nisto, relata Perius:

(…) o processo de ensino e aprendizagem aliado ao processo de experimentação – organização – construção, proporcionado pelo uso das mais diversas mídias, permite que o ambiente de possibilidades no ensino da Matemática pode ser favorecido e estendido, de forma a possibilitar maior autonomia no movimento da aprendizagem. A participação ativa do aluno é favorecida pelas tecnologias na informática, proporcionando assim, novas formas de aprendizagem, modificando as relações entre professores e alunos, ou entre alunos e alunos e entre alunos e conhecimento.²

A aula de Estatística, com o software de planilhas eletrônicas Microsoft Office Excel, pode despertar a atenção e a curiosidade dos estudantes, facilitando assim a exposição e o entendimento dos conceitos. Através do software, os dados podem ser analisados de forma prática, tornando assim, sua interpretação mais nítida, por meio do uso de diversos gráficos a serem, possivelmente, construídos sem dificuldade.

O presente artigo é um estudo das contribuições Microsoft Office Excel ao ensino de Estatística e tem como objetivo analisar as contribuições do software ao processo de ensino e aprendizagem de estatística, demonstrando também sua aplicabilidade. Podendo assim, ser base inspiradora, por parte dos professores, para a elaboração de aulas, com Excel, tendo o software como ferramenta para compreensão e relação com a Estatística.

METODOLOGIA

O presente artigo adotou, como estratégia metodológica, a pesquisa bibliográfica onde foram encontrados materiais que versam sobre o tema proposto, ou seja, sobre as contribuições do Excel ao ensino da estatística. Dessa forma, foi possível fazer uma análise das pesquisas já concluídas e, através dessa análise, listou-se as contribuições do software em estudo, para o ensino da Estatística. Além disso, através da versão 2010 e da versão Online do Excel, foi possível demonstrar, à priori, alguns de seus recursos.

DESENVOLVIMENTO

Ensinar Matemática não tem sido tarefa fácil, pois, a fim de que o aluno construa saberes, demonstre o interesse e a criatividade para este componente curricular, tornam-se razão de constante inquietude não só por parte do professor, como também, do sistema escolar. Diante desse contexto, a exigência do perfil de um professor que busque um ambiente de trabalho estimulante para que o aluno possa criar, comparar, defender e ampliar seus conhecimentos, garantindo assim a participação e interesse pela disciplina na qual está cursando, torna-se preeminente. Para isso, ele, o professor, agente mediador dos saberes escolares, precisa conhecer diversas possibilidades de trabalho e ferramentas tecnológicas que possam viabilizar uma aprendizagem significativa.

A Estatística, um dos ramos da matemática, é utilizada em várias áreas, como por exemplo, na realização de pesquisas, coleta de dados e interpretação dos resultados. O conhecimento estatístico é importante para sociedade, no sentido de concretizar em dados, pesquisas, tratar e sistematizar matematicamente informações relevantes. Exemplo desta amplitude do campo estatístico é a possibilidade dada ao cidadão de interpretar gráficos e tabelas, fazendo assim o uso inconsciente do conhecimento que adquiriu sobre a estatística. Além disso, as empresas necessitam de informações estatísticas para estudo de seus dados e uso na tomada de suas decisões. Segundo Lopes:

Não basta ao cidadão entender as porcentagens expostas em índices estatísticos, como o crescimento populacional, taxas de inflação, desemprego… É preciso analisar/relacionar criticamente os dados apresentados, questionando/ponderando até mesmo sua veracidade. Assim como não é suficiente ao aluno desenvolver a capacidade de organizar e representar uma coleção de dados, faz-se necessário interpretar e comparar esses dados para tirar conclusões.³

O ensino de Estatística é introduzido no Ensino Fundamental através dos Parâmetros Curriculares Nacionais que esclarece: “a finalidade é fazer com que o aluno venha a construir procedimentos para coletar, organizar, comunicar e interpretar dados, utilizando-se de tabelas, gráficos e representações que aparecem frequentemente em seu dia-a-dia.”⁴

No Ensino Médio, os alunos devem aprimorar seus conhecimentos sobre Estatística obtidos no Ensino Fundamental, neste sentido, as Orientações Curriculares para o Ensino Médio recomendam: “um trabalho com ênfase na construção e na representação de tabelas e gráficos mais elaborados, analisando sua conveniência e utilizando tecnologias, quando possível.”¹

As novas tecnologias e suas formas de interação estão presentes na vida das novas gerações seja através de aplicativos de mensagens, de serviços, de redes sociais e até mesmo de jogos. Como há uma familiaridade dos alunos com tecnologias fora do ambiente da escola, introduzi-la ao ensino da Estatística seria uma forma de dinamizar as aulas, tornando-as mais atraentes e inovadoras.

Os professores necessitam acompanhar a evolução da tecnologia, além de procurar sempre se capacitar com softwares que auxiliem no processo de ensino-aprendizagem dos alunos. Assim, após aprender a utilizar a tecnologia, o docente pode fazer uso da ferramenta para auxiliar o aluno com o entendimento do assunto. De acordo com Bianchini e col:

A ideia de que os alunos “dominam” o meio tecnológico é, muitas vezes, o que limita o uso de computadores como um recurso em sala de aula, uma vez que, em geral, os professores sentem-se muito limitados, o que pode deixar transparente, diante dos alunos, as suas fragilidades.⁵

As Orientações Curriculares para o Ensino Médio sugerem o uso de planilhas eletrônicas, apesar de sua criação não estar relacionada ao ensino, transformam-se em recursos tecnológicos úteis à aprendizagem Estatística no ambiente escolar. Esse documento¹ afirma que as planilhas eletrônicas são muito apropriadas para introduzir a noção de simulação probabilística, importante em diversos campos de aplicação.

Outro documento norteador, a Base Nacional Comum Curricular, apresenta em seu quadro de habilidades para o 6º ano do Ensino Fundamental, na unidade temática Probabilidade e Estatística, (EF06MA33) “… fazer uso de planilhas eletrônicas para registro, representação e interpretação das informações, em tabelas, vários tipos de gráficos e texto.”⁶

O EXCEL E O ENSINO DA ESTATÍSTICA

O editor de planilhas, Microsoft Office Excel ou simplesmente Excel, é um dos principais softwares recomendados para o uso no ensino da Estatística. Este software possui uma interface amigável e de fácil utilização. Quanto mais recente sua versão, mais simples se torna o uso das ferramentas disponíveis, devido a suas constantes atualizações de layout.

Como toda tabela, a planilha eletrônica é composta por linhas (representadas por números) e colunas (representadas por letras). A interseção entre uma linha e uma coluna se chama célula. Na célula, podem ser inseridos títulos, descrições de dados, dados, funções, entre outros. As funções vão de simples cálculos, tais como soma de um intervalo, a cálculos mais complexos, como o cálculo de quartis e percentis. Ao inserir dados sobre determinado estudo, o aluno pode analisá-los tirar média, mediana, desvio padrão, além de criar gráficos e tabelas.

Além das versões para desktop, que são pagas, há versão do Excel Online que pode ser acessada através do navegador de forma gratuita e online. Nela, o aluno poderá trabalhar em tempo real, de forma sincrônica a outras pessoas, na escola ou em casa. Para acessá-lo, o usuário necessita do endereço de e-mail no Outlook (adquirido gratuitamente). Ao abrir o e-mail, basta clicar no botão do canto superior esquerdo, onde estão os aplicativos, em seguida, no ícone do Excel. Após isso, basta abrir um trabalho em branco, clicando em “Nova pasta de trabalho em branco”.

GRÁFICOS

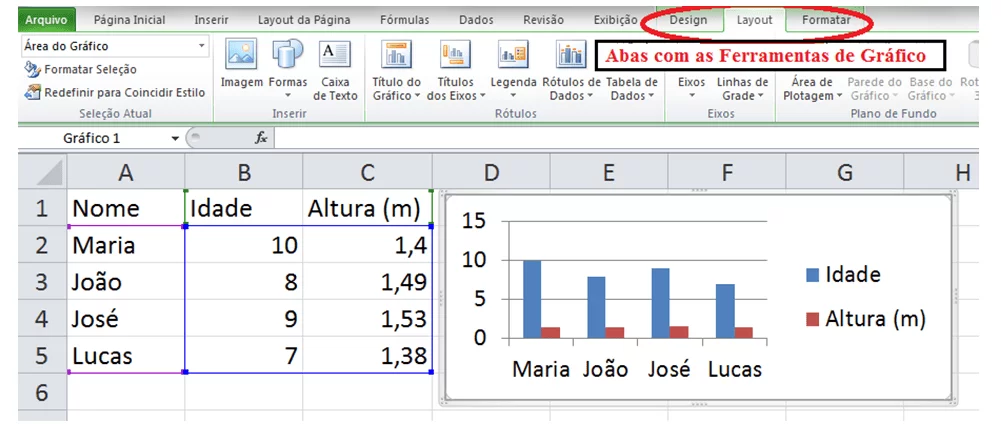
A partir de uma tabela com dados inseridos no Excel, é possível criar diversos tipos de gráficos, como por exemplo, os de coluna, de linha, de setores, de barra e de área, que são disponibilizados pelo software. Para inseri-los, seleciona-se a tabela desejada, clica-se em “Inserir” e escolhe-se o gráfico desejado. Depois de inserido, como mostra a Figura 1, na aba “Layout” é permitido fazer alterações em seu título, legenda, cores das variáveis, entre outros.

Na fase de análise de uma pesquisa, a interpretação da informação investigada se torna mais fácil ao criar-se um gráfico, pois, os dados são apresentados de forma clara e objetiva (Figura 1). Os Parâmetros Curriculares Nacionais afirmam que “ao trabalhar com o Tratamento da Informação é fundamental ainda que, ao ler e interpretar gráficos, os alunos se habituem a observar alguns aspectos que permitam confiar ou não nos resultados apresentados.”⁴

Figura 1 – Editando o gráfico no Microsoft Office Excel 2010.

FUNÇÕES

Sobre o uso do software em aula, Bianchini complementa: “(…) pode-se afirmar que este recurso computacional contribuiu para que o centro do processo fosse a interpretação e as inter-relações possíveis a respeito do fenômeno pesquisado, minimizando o tempo dos cálculos e traçado de tabelas e gráficos.”⁵

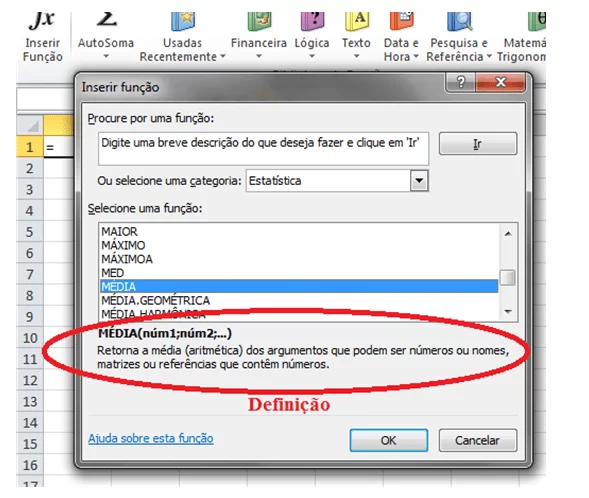
A ferramenta do Excel chamada “função” oferece fórmulas pré-definidas que, após inserção de valores e critérios, obtêm-se o cálculo solicitado. Há categorias de funções no software, algumas delas, são as funções estatísticas. Para ter acesso a essas funções, clica-se no botão de função. Na janela aberta estão as categorias, ao selecionar estatística, são expostas as funções dessa categoria disponíveis. Quando se seleciona uma função, na parte inferior da janela, estará sua definição (Figura 2). As funções podem ser inseridas pelo botão função ou podem ser digitadas diretamente na célula.

Figura 2 – Inserindo função no Microsoft Excel 2010.

No ensino da Estatística, as funções podem ser usadas para calcular as medidas de posição, medidas de dispersão, tabelas de frequência, cálculos de probabilidade, entre outros. Ao inserir dados no Excel, a compreensão do aluno, a cerca do conteúdo abordado, torna-se mais significativa, acessível e prática. Após o uso das funções, o aluno obtém os resultados através de gráficos. Nesse contexto, Morais afirma que:

O Excel se mostra um excelente recurso para abreviar cálculos repetitivos, que não contribuem para a compreensão dos conceitos trabalhados em probabilidade e estatística, possibilitando que o tempo disponível para se trabalhar esses conteúdos possa ser mais direcionado para a simulação de experimentos e análise de dados organizados na forma de tabelas e gráficos, sem que esse trabalho se torne cansativo e desmotivador para eles.⁷

MEDIDAS DE POSIÇÃO

A tomada de decisão com base em pesquisas estatísticas perde o sentido quando há apenas a representação gráfica, é necessário que sejam realizadas análises das medidas de posição. Segundo Morais, essas medidas “(…) permitem sintetizar as informações coletadas sobre a variável em estudo.”⁷

Para demonstrar algumas das medidas de posição no Excel, utilizou-se o conjunto de dados fictícios que representam as notas do ENEM de 10 alunos de uma determinada escola: 642, 468, 642, 548, 632, 532, 642, 658, 677 e 701. O título “Notas do ENEM” ficou na célula A1 e os valores das notas distribuídos entre as células A2 e A11.

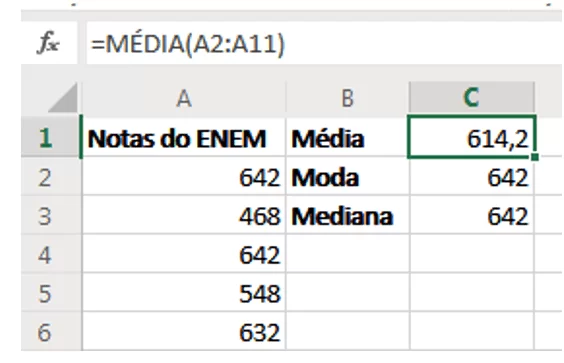
Para calcular a média dos dados informados, no Excel Online, foi utilizada a função MÉDIA que calcula a média (aritmética) dos dados inseridos. Dessa forma, foi escolhida a célula B1 para o nome da medida “Média” e a célula C1 para a função =MÉDIA(A2:A11), na qual “A2:A11” é o intervalo que se encontram os dados.

Para calcular a moda, foi utilizada a função MODO.ÚNICO, que calcula os valores que ocorrem com maior frequência. Foi escolhida a célula B2 e C2, para o nome da medida e a fórmula, respectivamente. Na célula C2 foi inserida a função =MODO.ÚNICO(A2:A11).

A mediana foi calculada com função MED que calcula a mediana, ou seja, calcula o número central de um determinado conjunto de números. Como mostra a Figura 3, na célula B3 foi inserida o nome da medida e na célula C3 foi inserida a função =MED(A2:A11).

Figura 3 – Inserindo a média, moda e mediana no Excel Online.

A função para calcular a moda é diferente em algumas versões do Excel. Na versão 2003 é a função MODO, na versão 2010 e na versão online é a função MODO.ÚNICO. A descrição na janela de funções ajuda a identificar se a função corresponde ao cálculo esperado.

Ainda no Excel Online, para calcular o 1º, 2º e 3º quartis dos dados, insere-se a função QUARTIL.EXC digitando na célula =QUARTIL.EXC (“intervalo de dados”; “quartil desejado (de 0 a 4)”). Para calcular o 3º quartil, por exemplo, foi inserida a função =QUARTIL.EXC(A2:A11;3), na qual o intervalo de dados utilizados foi “A2:A11” e o quartil desejado 3. Como mostra a Figura 4, essa função foi inserida na célula C4.

Os percentis dos dados foram calculados através da função PERCENTIL.EXC digitando na célula =PERCENTIL.EXC(“intervalo de dados”; “percentil desejado (de 0 a 1)”). Na Figura 4 foi calculado o 45º percentil e a célula C5 foi escolhida pra ser inserida a função =PERCENTIL.EXC(A2:A11;0,45), na qual o intervalo de dados utilizados foi “A2:A11” e o percentil desejado 45.

Figura 4 – Inserindo quartil e percentil no Excel Online.

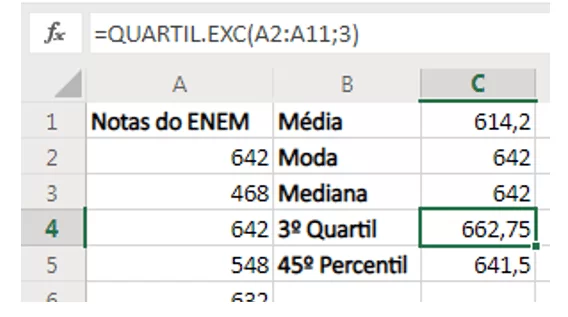
O valor mínimo é encontrado através da função MÍNIMO, ao calcular o 0 quartil ou ao calcular o 0 percentil, a mediana é encontrada através da função MED, ao calcular o 3º quartil ou ao calcular o 50º percentil e o valor máximo é encontrado através da função MÁXIMO, ao calcular o 4º quartil ou ao calcular o 100º percentil.

MEDIDAS DE DISPERSÃO

Segundo Morais “(…) com o auxílio do Excel os cálculos do desvio padrão se tornam fáceis e rápidos, basta selecionar as colunas e utilizar as ferramentas de cálculo do programa, e o coeficiente de variação pode ser obtido como uma calculadora simples.”⁷

Existem duas formas para calcular a variância: usando a função VAR.A, que estima a variação com base em uma amostra e a função VAR.P que calcula a variação com base na população total. Devido ao caráter de amostra dos dados, foi calculada (Figura 5) a variância amostral na célula C6 e utilizou-se a função VAR.A digitando =VAR.A(A2:A11), na qual “A2:A11” é o intervalo em que se encontram os dados.

Figura 5 – Inserindo variância e desvio padrão no Excel Online.

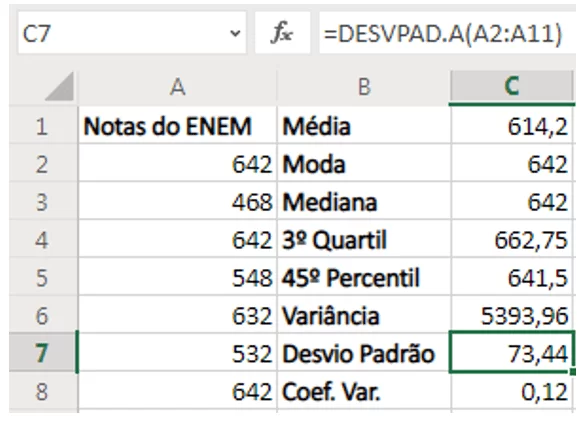
Assim como na variância, para o cálculo do desvio padrão há duas formas: usando a função DESVPAD.A que calcula o desvio padrão a partir de uma amostra e a função DESVPAD.P que calcula o desvio padrão com base na população total determinada como argumento. Como os dados são uma amostra, para calcular o desvio padrão amostral foi inserida a função DESVPAD.A na célula C7, como mostra a Figura 5, digitando =DESVPAD.A (A2:A11), onde “A2:A11” é o intervalo que se encontram os dados. Como o coeficiente de variação é a razão entre o desvio padrão pela média, para calculá-lo inseriu-se uma operação matemática simples de divisão “=C7/C1” na célula C8, onde C7 é o valor do desvio padrão e C1 é o valor da média.

As experiências de Nascimento⁸ o fez constatar a necessidade de explorar softwares, uma vez que medidas estatísticas são muito utilizadas nas mídias escritas e em livros didáticos:

Por isso, devemos relacionar as informações do cotidiano com Softwares computacionais para que possam dar significado aos dados nos resultados das pesquisas desenvolvidas por eles. Pois os Softwares computacionais auxiliam os alunos na visualização dos questionamentos, ajudando-os na interpretação das situações problemas, deixando-os despreocupados em relação aos cálculos, pois é mais importante a análise dos questionamentos seguindo todas as etapas da pesquisa, do que deter-se a cálculos meramente repetitivos.⁸

CONSTRUÇÃO DE TABELA DE FREQUÊNCIA

O Excel auxilia também na construção de tabela de frequências. Essa tabela permite a organização dos dados e a realização de interpretação rápida e resumida dos resultados de uma pesquisa.

Para demonstrar a construção de tabela de frequência, foi utilizado o conjunto de dados fictícios que representam a idade de 10 alunos de uma determinada escola: 15, 14, 16, 15, 14, 13, 16, 15, 15 e 14. O título “Altura dos Alunos” consta na célula A2 (Figura 6), os valores das idades foram devidamente distribuídos entre as células A3 e A12, “Classes” na célula B2, as classes 13, 14, 15 e 16 distribuídas da célula B3 a B6, o título da frequência absoluta “Freq. Abs.” na célula C2 e o título da frequência relativa “Freq. Rel.” na célula D2.

Figura 6 – Inserindo a Frequência Absoluta no Excel Online.

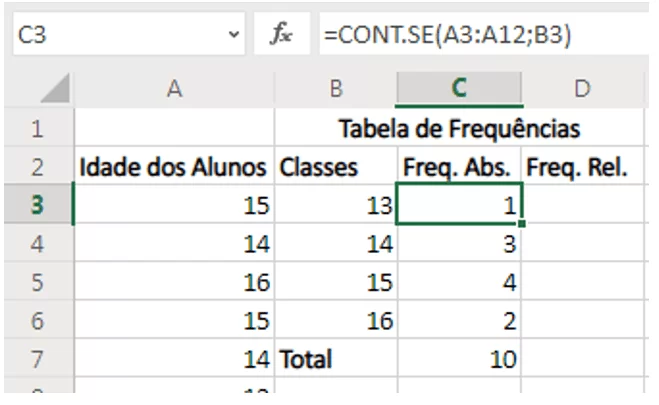
Para calcular a frequência absoluta, foi utilizada a função CONT.SE que calcula o número de células não vazias em um intervalo que corresponde a uma determinada condição. Para utilizar essa função, digita-se =CONT.SE(“intervalo desejados”; ”critérios”). Para cada classe, deve-se inserir uma função obedecendo seu critério, o intervalo desejado será o mesmo para todas as classes “A3:A12”, o critério será o valor da classe referente a frequência calculada.

Como mostra na Figura 6, para a célula C3 foi digitada a função =CONT.SE (A3:A12;B3), utilizando o intervalo desejado e o critério da classe localizada a sua esquerda. Para as células C4, C5 e C6 utilizou-se a mesma função, mudando apenas o critério para B4, B5 e B6 respectivamente. Na célula C7 foi inserida a função SOMA para somar as classes obtidas no intervalo “C3:C6”, digitando =SOMA (C3:C6).

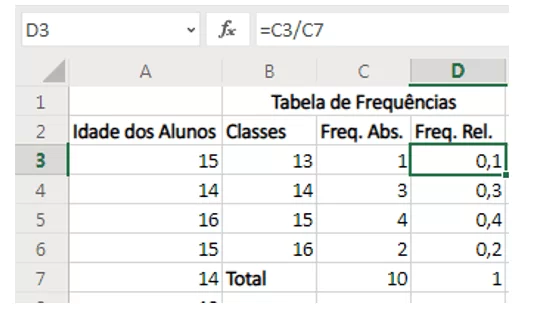
A frequência relativa não foi calculada com função, mas sim com operação matemática simples disponível pelo Software. Como a frequência relativa é o quociente entre a frequência absoluta e a soma da frequência absoluta, foi utilizada uma simples operação de divisão, como mostra a Figura 7. No caso da célula D3, digitou-se =C3/C7, onde C3 é a frequência absoluta, localizada na esquerda da célula D3, e C7 é a soma da frequência absoluta. Para as células D4, D5 e D6 foram utilizadas a mesma operação, mudando apenas o dividendo pelas células C4, C5 e C6, respectivamente.

Figura 7 – Inserindo a Frequência Relativa no Excel Online.

DADOS BIVARIADOS

O software permite que sejam feitas análises de duas variáveis sobre o mesmo indivíduo da amostra. Para demonstrar o estudo de dados bivariados, utilizou-se os mesmos dados fictícios utilizados anteriormente, notas do ENEM de 10 alunos de uma determinada escola: 642, 468, 642, 548, 632, 532, 642, 658, 677 e 701. O título “Notas do ENEM” ficou na célula A1 e os valores das notas distribuídos da célula A2 a A11 e a idade de 10 alunos de uma determinada escola: 15, 14, 16, 15, 14, 13, 16, 15, 15 e 14. O título “Altura dos Alunos” ficou na célula B1 e os valores das notas distribuídos da célula B2 a B11.

Para inserir o gráfico de dispersão, foram selecionadas as células onde se encontram as informações e clicou-se em Gráfico, depois em Dispersão (Figura 8).

Figura 8 – Inserindo diagrama de dispersão no Excel Online.

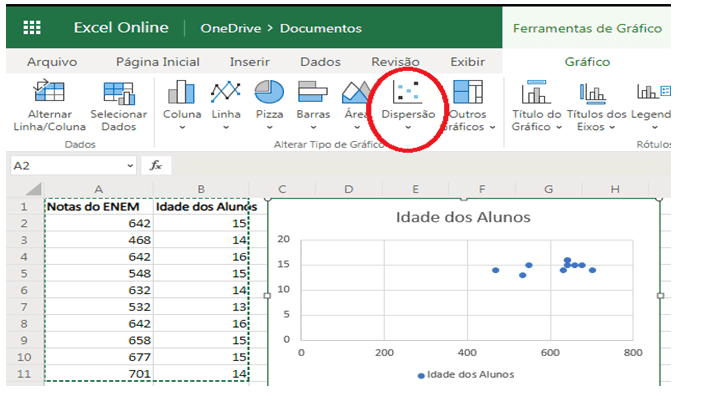
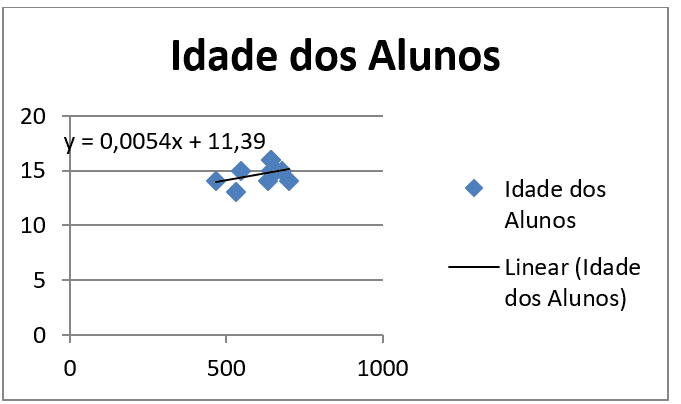
Seguindo os mesmos passos, agora no Microsoft Excel 2010, é possível encontrar a reta de regressão linear (Figura 9). Seleciona-se o gráfico de dispersão, na barra de ferramentas, em Ferramentas de Gráficos clica-se em “Layout”, depois em “Linha de Tendência”, “Mais Opções de Linha de Tendência…”, na janela aberta seleciona-se “Linear” em Tipo de Tendência/Regressão, mais abaixo da janela, seleciona-se “Exibir Equação no Gráfico”, concluindo enfim ao fechar a janela. O Resultado obtido será:

Figura 9 – Inserindo reta de regressão no Microsoft Excel 2010.

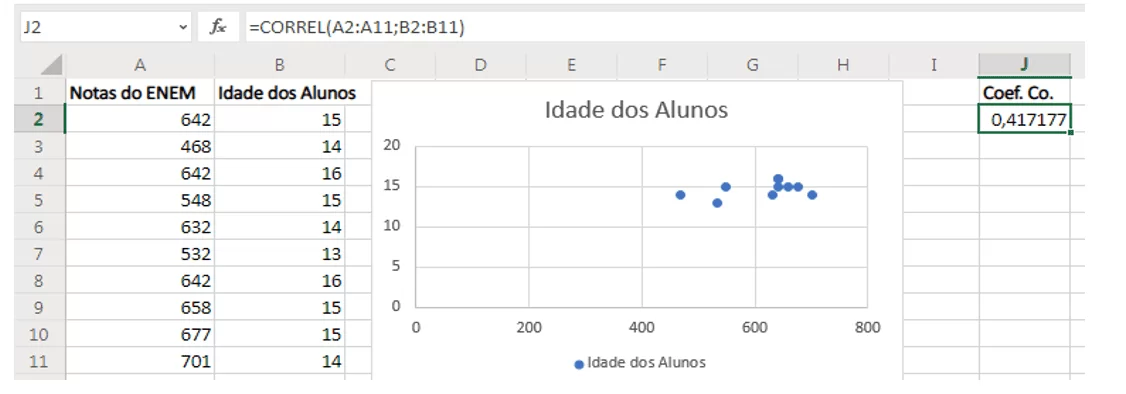
O coeficiente de correlação entre dois conjuntos de dados é calculado ao utilizar-se função CORREL. Na célula J2 (Figura 10) digitou-se =CORREL(A2:A11;B2:B11), onde “A2:A11” é o intervalo de dados das Notas do ENEM e “B2:B11” é o intervalo de dados das Idades dos Alunos.

Figura 10 – Inserindo coeficiente de correlação no Excel Online.

FERRAMENTA ANÁLISE DE DADOS

Para realizar análises estatísticas é possível economizar etapas e tempo usando as Ferramentas de Análise. Através dos dados e parâmetros fornecidos para cada análise, a ferramenta utiliza as funções estatísticas para calcular e exibir os resultados em uma tabela de saída. Algumas ferramentas geram gráficos, além das tabelas de saída.

Essa ferramenta não está disponível no Excel Online e tem que ser ativada nas versões para desktop. Para ativá-la no Microsoft Excel 2010, clica-se na guia “Arquivo”, “Opções” e em seguida, na categoria “Suplementos”. Em “Gerenciar”, seleciona-se “Suplementos do Excel” e clica-se em “Ir”. Na caixa “Suplementos”, marca-se a caixa “Ferramentas de Análise” clicando posteriormente em “OK”.  Caso surja o aviso de que as Ferramentas de Análise não estão atualmente instaladas no computador, deve-se clicar em “Sim” para instalá-las.

A ferramenta “Análise de Dados” está disponível no lado direito da barra de ferramentas na aba “Dados”. Clicando-se em “Análise de Dados”, uma janela fica exposta com os cálculos disponíveis, entre eles Correlação, Covariância, Histograma, Ordem e Percentil, Estatística Descritiva e Regressão.

Para demonstrar a ferramenta, foi utilizado o conjunto de dados fictícios que representam a idade de 10 alunos de uma determinada escola: 15, 14, 16, 15, 14, 13, 16, 15, 15 e 14. O título “Altura dos Alunos” ficou na célula A1 (Figura 11), os valores das idades distribuídos da célula A2 a A11.

Para utilizar a Estatística Descritiva, clica-se em sua opção na janela de Análise de Dados e depois em “OK”. Na janela “Estatística descritiva” foi selecionado da célula A2 a A11 o Intervalo de entrada, marcada a opção “Intervalo de saída” e selecionado um intervalo qualquer na planilha a fim de expor a tabela com o resultado dos cálculos. Além disso, foram marcadas as opções “Resumo Estatístico” e “Nível de confiabilidade p/ média”.

Figura 11 – Inserindo a função de Análise de Dados no Microsoft Excel 2010.

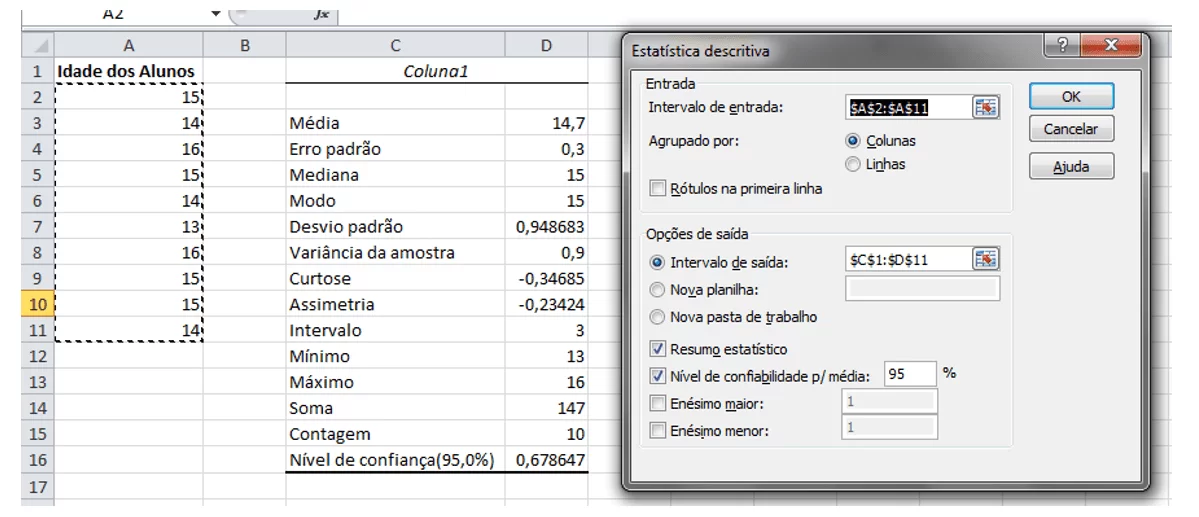
Como ilustra a Figura 11, o resultado da opção Estatística Descritiva calcula automaticamente Média, Erro padrão, Mediana, Modo, Desvio padrão, Variância da amostra, Curtose, Assimetria, Intervalo, Mínimo, Máximo, Soma, Contagem e Nível de confiança (95,0%).

CONSIDERAÇÕES FINAIS

Com o avanço da tecnologia a tendência das escolas públicas ou privadas, é se apropriar dos saberes e habilidades necessárias para manusear alguns desses dispositivos tecnológicos, no sentido de facilitar o dia a dia da população ou de um determinado grupo social. Esse contexto desafia as escolas e os professores a respeito do uso desses dispositivos de forma a auxiliarem no processo de ensino-aprendizagem. Dessa forma, a escola não deve impedir a presença da tecnologia, mas sim utilizar o ambiente escolar para estimular e educar seus alunos para o uso adequado dos recursos tecnológicos.

O Excel é uma ferramenta que não deixou de ser utilizada e por possuir recursos indispensáveis, é útil tanto no mercado de trabalho, quanto no meio educacional. Esse software é um ótimo recurso didático para aulas de matemática, devido à quantidade de fórmulas e funções disponíveis para serem utilizados.

Verificou-se, ao longo da pesquisa, que no ensino da Estatística, o Excel possui diversas aplicações que podem contribuir para o processo de ensino-aprendizagem, desde o fundamental até o ensino superior. A compreensão dos conceitos trabalhados se torna mais eficaz, pois os alunos focarão mais na análise e interpretação dos dados trabalhados, perdendo menos tempo com os cálculos repetitivos, que não colaboram para a compreensão e consolidação dos conceitos estudados.

Durante a redação do texto, foram demonstradas algumas funções e utilidades deste software. É notável que não é necessário ter um conhecimento aprofundado de informática para fazer o uso de seus recursos. É bastante acessível e sua caixa de ferramentas possui suas utilidades mais usadas. Para um melhor aproveitamento do Excel no ensino da Estatística, faz-se necessário que os professores estejam devidamente capacitados para utilizá-lo. De forma que os professores sejam capazes de tirar eventuais dúvidas, por parte dos alunos, de forma clara e que permitam que eles também façam um bom uso do mesmo.

REFERÊNCIAS

BIANCHINI, Daiani Finatto; BISOGNIN, Cleber; SOARES, Débora da Silva. Uma proposta didática para o ensino de estatística: o uso do excel para representação gráfica. RENOTE: revista novas tecnologias na educação, Porto Alegre, v. 13, n. 2, 2015. Disponível em: https://seer.ufrgs.br/renote/article/view/61431o. Acesso em: 07 de janeiro de 2019.

BORBA, Rute Elizabeth de Souza; MONTEIRO, Carlos Eduardo; GUIMARÃES, Gilda Lisboa; COUTINHO, Cileda; KATAOKA, Verônica Yumi. Educação Estatística no Ensino Básico: currículo, pesquisa e prática em sala de aula. Em Teia – Revista de Educação Matemática e Tecnológica Iberoamericana. Recife, v. 2, n. 2, 2011. Disponível em: https://periodicos.ufpe.br/revistas/emteia/article/view/2153. Acesso em: 07 de janeiro de 2019.

BRASIL. Base Nacional Comum Curricular. Brasília: MEC/Secretaria de Educação Básica, 2018.

BRASIL. Orientações Curriculares para o Ensino Médio. Brasília: Ministério da Educação, Secretaria de Educação Básica, 2006, v. 2 – Ciências da Natureza, Matemática e suas Tecnologias.

BRASIL. Parâmetros Curriculares Nacionais: Matemática. Brasília: Ministério da Educação, Secretaria do Ensino Fundamental, 1997.

EXCEL ONLINE. Disponível em: https://office.live.com/start/Excel.aspx. Acesso em 15 de janeiro de 2019.

GAROFALO, Débora. Como usar o Excel para ensinar Matemática. Nova Escola, 2018. Disponível em: https://novaescola.org.br/conteudo/11622/como-usar-o-excel-para-ensinar-matematica?download=true#. Acesso em: 06 de janeiro de 2019.

LOPES, Celi Espasandin. O ensino da estatística e da probabilidade na educação básica e a formação dos professores. Cad. Cedes, Campinas, v. 28, n. 74, p. 57-73, jan/abr. 2008.

MICROSOFT OFFICE. Usar Ferramentas de Análise para executar análises de dados complexas. Disponível em: https://support.office.com/pt-br/article/usar-ferramentas-de-an%C3%A1lise-para-executar-an%C3%A1lises-de-dados-complexas-6c67ccf0-f4a9-487c-8dec-bdb5a2cefab6. Acesso em: 09 de março de 2019.

MORAIS, Sílvia Cristina Dornelas de. EXCEL: uma alternativa para o ensino de probabilidade e estatística. 2016. 51 f. Dissertação (Mestrado Profissional em Matemática em Rede Nacional) – Universidade Federal de Goiás, Goiânia, 2016.

NASCIMENTO, João Leno do. A utilização do Excel para o ensino de estatística no Ensino Médio: um estudo de caso no município de Mamanguape. Trabalho de Conclusão de curso – Universidade Federal da Paraíba, João Pessoa, 2016.

NAVES, Antonio César de Mesquita. Estatística Básica com Planilha Eletrônica. Dissertação (Mestrado em Matemática – ProfMat), Universidade do Estado de Mato Grosso, Sinop, Mato Grosso. 2018.

PERIUS, Ana Amélia Butzen. A tecnologia aliada ao ensino de matemática. Trabalho de Conclusão de Especialização. Universidade Federal do Rio Grande do Sul, Rio Grande do Sul, 2012.

^[1] Graduação em Licenciatura Plena em Matemática.

^[2] Doutorado em Engenharia de Processos. Mestrado em Biometria e Estatística Aplicada. Especialização em Fundamento e Ensino de Matemática. Graduação em andamento em Ciência da Computação. Graduação em Ciências com Hab. em Matemática.

^[3] Doutor em Engenharia de Processos. Mestrado em Ensino das Ciências. Graduação em Matemática.

Enviado: Junho, 2019.

Aprovado:  Janeiro, 2020.