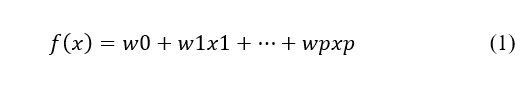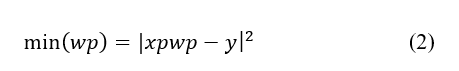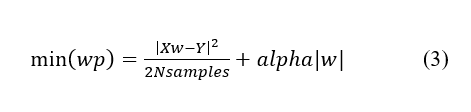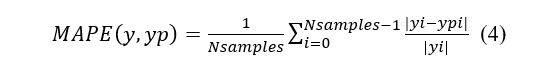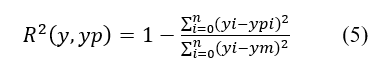ARTIGO ORIGINAL
SILVA, Maycon Gabriel Gomes da [1], ROCHA, Douglas Abreu da [2], PEIXOTO, Zélia Myriam Assis [3]
SILVA, Maycon Gabriel Gomes da. ROCHA, Douglas Abreu da. PEIXOTO, Zélia Myriam Assis. Metodologia para análise limnológica: estudo de caso em três marias – MG – Brasil. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 12, Vol. 08, pp. 55-80. Dezembro de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/tecnologia/analise-limnologica, DOI: 10.32749/nucleodoconhecimento.com.br/tecnologia/analise-limnologica
RESUMO
O método tradicional de avaliação da qualidade da água em reservatórios hídricos, o qual consiste basicamente na coleta de amostras de água e análises laboratoriais, é um método caro e ineficaz para o diagnóstico dos problemas relacionados à qualidade da água nas bacias hidrográficas e reservatórios, devido, principalmente, ao alto custo no monitoramento, interrupção nas campanhas de coleta de amostra de água por falta de verbas e falta de procedimento padronizado no Brasil. O sensoriamento remoto, através de algoritmos de regressão, processamento digital de imagens e técnicas de machine learning, são tecnologias usadas para monitorar reservatórios hídricos. O objetivo deste trabalho é o desenvolvimento de uma metodologia para análise limnológica da qualidade da água em reservatórios hídricos a partir de imagens do satélite Landsat 8 OLI e a aplicação de técnicas de machine learning, baseadas em regressão linear e regressão LASSO (Least Absolute Shrinkage and Selection Operator). Nesse contexto, foi realizado um estudo de caso no Reservatório de Três Marias/MG, onde foi feita a predição dos parâmetros limnológicos turbidez e sólidos totais para a validação da metodologia proposta. Essa metodologia consiste em usar dados históricos de parâmetros limnológicos da qualidade da água, informações espectrais das imagens do satélite Landsat 8 OLI, fazer o pré-processamento destes dados e utilizá-los no treinamento de modelos obtidos a partir das técnicas de regressão linear e regressão LASSO, gerando-se um modelo de predição que é disponibilizado por meio de uma plataforma web. O treinamento e teste dos modelos de regressão linear e LASSO foram realizados a partir de dados de medições in loco anteriores do Reservatório de Três Marias – MG, disponibilizados pela Companhia Energética de Minas Gerais S.A. (CEMIG). A validação dos modelos foi realizada por meio das métricas estatísticas coeficiente de determinação, erro percentual absoluto médio, erro absoluto médio, onde os principais resultados foram 0,832, 0,087 e 1,938 respectivamente. Vale ressaltar que a metodologia proposta pode ser estendida a qualquer reservatório desde que estejam disponíveis dados históricos dos parâmetros limnológicos e informações espectrais das bandas do satélite Landsat 8 OLI.
Palavras-chave: Google Engine Earth, Parâmetros limnológicos, Machine learning, Sensoriamento remoto, Modelos de regressão.
1. INTRODUÇÃO
Água é uma substância química de vital importância para os seres vivos, fundamental às suas reações bioquímicas interiores e no seu entorno, em suas relações sociais e com a natureza. Nesse sentido, pode-se observar, historicamente, que as grandes civilizações se desenvolveram ao longo dos rios como os egípcios, dentre muitas outras, utilizando a água como alimento, meio de transporte, comércio e desenvolvimento (MOTA; BRAICK, 2002).
Nas últimas décadas, o problema da poluição hídrica tem se tornado cada vez mais significativo e uma das principais causas são os rejeitos industriais liberados diretamente no ambiente, o grande fluxo de esgoto doméstico das zonas urbanas e as erosões próximas aos leitos dos rios, decorrentes do manejo inadequado das matas ciliares e má utilização das regiões de proteção ambiental.
Os parâmetros limnológicos são usados para avaliar o nível de poluição ou eutrofização dos lagos e reservatórios, denominada água bruta, ou seja, da água que é captada pelas empresas responsáveis pelo abastecimento das cidades e áreas agrícolas, têm que apresentar um nível mínimo de qualidade segundo os protocolos dos órgãos reguladores para que possa ser tratada e disponibilizada para a população (ANA, 2019).
Como a qualidade e degradação das águas de lagos e represas precisam ser monitoradas com frequência, os métodos tradicionais que envolvem a coleta in situ e análises em laboratórios são, normalmente, de alto custo e demorados. É, nesse contexto, que o sensoriamento remoto, informações espectrais de imagens de satélite e dados históricos do reservatório, podem ser usados como uma ferramenta auxiliar e acessível no processo de monitoramento da qualidade da água de reservatórios hídricos.
Vários estudos voltados para a análise da qualidade da água estão disponíveis na literatura atual, dentre os quais existem propostas voltadas ao uso de sensoriamento remoto, redes neurais artificiais e machine learning para fazer análise e monitoramento de parâmetros limnológicos da qualidade da água.
Em Silva et al. (2021), os autores apresentam o desenvolvimento de uma proposta para a avaliação da qualidade da água de bacias hidrográficas com base em técnicas de processamento digital aplicadas a imagens de satélite. Dentre as técnicas de processamento de imagens utilizadas destacam-se a limiarização pelo Método de Otsu, binarização, expansão linear por saturação, Filtro Laplaciano, extração de características por meio de matrizes de co-ocorrência e classificação pelo Discriminante de Bayes. Essas técnicas também foram implementadas em uma plataforma computacional em ambiente MATLAB®, responsável pela interface entre o sistema e os usuários. O sistema proposto apresentou uma taxa de sucesso aproximada de 70% quanto à classificação dos índices de qualidade da água.
Batur e Maktav (2019) usam imagens dos satélites Landsat 8 e Sentinel 2A para estabelecer a relação entre os parâmetros de qualidade da água e a refletância espectral e validar os valores da qualidade da água de superfície usando o Support Vector Machine (SVM), entre outros métodos.
Qi et al. (2020) propõem monitorar quatro parâmetros de qualidade da água (PH, DO, CODMn e NH3-H) com base na rede LSTM (Long Short-Term Memory), de 2013 a 2018, no Lago Taihu, China. O modelo obtido foi utilizado para determinar os parâmetros de qualidade da água e aplicado a imagens de satélite ao longo de vários períodos para medir o parâmetro de qualidade da água relacionado a cada pixel e as mudanças na qualidade da água.
Aldhyani (2020) usam algoritmos de inteligência artificial para prever WQI (índice de Qualidade da água) e WQC (Classificação da Qualidade da Água) com base em 7 parâmetros de dados coletados em diferentes estados indianos de 2005 a 2014, que estão disponíveis no Kaggle. As redes NARNET (Nonlinear Autoregressive Neural Network) e LSTM foram utilizadas para a fase de previsão do WQI. Para a fase WQC, foram utilizadas as técnicas SVM, K-Nearest Neighbor (KNN) e Naïve Bayes para classificar os dados em 5 classes (Excelente, Bom, Ruim, Muito Ruim e Inadequado para beber).
Com base na região da Bacia do Lago Ebinur na China, Li et al. (2021) aplicam quatro algoritmos de aprendizado de máquina para modelar e prever o WQI de 9 WQP’s (parâmetro de qualidade da água), sensoriamento remoto de banda espectral e índice espectral de modelagem 2D usando dados do Sentinel-2 MSI.
Em Lobo et al. (2021), os autores tratam da predição da clorofila-a (Chl-a) e do índice de estado trófico (TSI) usando imagens do sentinel-2 MSI e dados coletados in situ. Foi implementado um aplicativo no Google Engine Earth (GEE) onde os usuários podem adicionar informações e fazer o acesso aos resultados em vários reservatórios no Brasil e na América Latina. A metodologia proposta utiliza imagens do satélite Sentinel-2 corrigidas para efeitos atmosféricos e de reflexo solar, de forma a gerar uma coleção de imagens do Índice de Clorofila-a Diferença Normalizada (NDCI) para toda a série temporal de uma determinada área. Os dados NDCI recuperados das imagens são, então, comparados com Chl-a medido in situ. O NCDI é usado para estimar a concentração de Chl-a, com base em um modelo de ajuste não linear e o índice TSI é processado com base em um modelo de árvore de decisão que classifica cada pixel em cinco níveis para o Índice de Estado Trófico (Oligo, Meso, Eutrófico, Super e Hipereutrófico). As etapas de processamento são compostas pela correção atmosférica baseada no método Satellite Invariant Atmospheric Correction (SIAC), correção do efeito do reflexo do sol e exclusão dos pixels com nuvens, aplicando-se os produtos Sentinel-2 (Probabilidade de nuvem para a máscara de água) e Máscara de água do Joint Research Centre (JRC), disponíveis no GEE. Os resultados obtidos pelo modelo final indicam um coeficiente de determinação de 0,86 e um erro percentual médio absoluto (MAPE) próximo de 90%.
O objetivo deste trabalho é desenvolver uma metodologia capaz de fazer predições de parâmetros limnológicos de qualidade da água, disponibilizada através de uma plataforma web. Com base nas técnicas de regressão linear e regressão LASSO para fazer a predição dos parâmetros limnológicos da qualidade da água, usando informações espectrais das bandas 1, 2, 3, 4, 5, 6, 7 do satélite Landsat 8 OLI e dados históricos dos parâmetros limnológicos do Reservatório de Três Marias/MG. Os modelos são treinados e submetidos à etapa de testes, quando predições são realizadas com base em novos dados limnológicos e informações espectrais das bandas do Landsat 8 OLI. Para a realização de novas predições foi, então, desenvolvida a plataforma web, disponível no link http://plattform.herokuapp.com/, juntamente com as instruções necessárias à sua utilização.
2. DESENVOLVIMENTO
Nesta seção serão apresentados os principais conceitos das técnicas e métodos utilizados neste trabalho, técnicas relacionadas ao sensoriamento remoto para a predição de alguns parâmetros limnológicos, técnicas de machine learning, Google Engine Earth, dentre outros tópicos que compõem a metodologia.
2.1 LIMNOLOGIA DA ÁGUA
Conforme Tundisi (2008), a limnologia baseia-se em análises recursos hídricos do planeta, incluindo reservas de água doce e salina, áreas pantanosas dentre outras, nos diversos ecossistemas, essas análises envolvem duas características que compreendem a descrição dos componentes abióticos e suas propriedades (fatores físicos e químicos, concentrações, intensidades) e a avaliação das comunidades bióticas. A análise das inter-relações funcionais em um ecossistema inclui a investigação dos elementos responsáveis pelos ciclos de materiais, os processos dinâmicos nos sistemas abióticos, as relações dos organismos com os fatores ambientais e as relações dos organismos entre si, cujos resultados são as sínteses limnológicas.
2.2 SENSORIAMENTO REMOTO DA ÁGUA
Para trabalhar com sensoriamento remoto para análise de ambientes aquáticos é necessário entender que o fluxo de energia radiante que atravessa a interface ar/água está sujeito a dois processos principais: absorção e espalhamento. Esses processos são quantificados através de coeficientes específicos que, por sua vez, são conhecidos como propriedades ópticas inerentes do corpo d’água. Essas propriedades dependem somente do meio em questão, sendo os valores dos coeficientes de absorção e espalhamento diretamente relacionados à presença, tipo e concentração de substâncias chamadas compostos opticamente ativos (COAs), os quais afetam o espectro de absorção e espalhamento da água pura, podendo ser formados por partículas em suspensão, organismos vivos e substâncias orgânicas dissolvidas.
De acordo com Jensen (2011), em estudos que visam à aplicabilidade de sensoriamento remoto para corpos d’água, é primeiramente útil entender como a água pura seletivamente absorve e/ou espalha a radiação incidente ou a luz solar descendente na coluna d’água. Ainda, é importante considerar como a luz incidente é afetada quando a coluna da água não é pura, mas contém materiais orgânicos e inorgânicos.
Ainda, segundo Jensen (2011), a característica mais notável do comportamento espectral da água pura é que a quantidade mínima de absorção e espalhamento da luz incidente na coluna d’água ocorre na região do comprimento de onda da cor azul (0,4 a 0,5 µm), com o valor mínimo localizado em aproximadamente 0,46 – 0,48 µm.
As substâncias presentes na água são determinantes para sua análise, pois determinam a composição da água no momento em que é feita a coleta de dados. Assim, em termos do monitoramento por sensoriamento remoto, os comportamentos espectrais dessas substâncias devem ser considerados (VILELA, 2010).
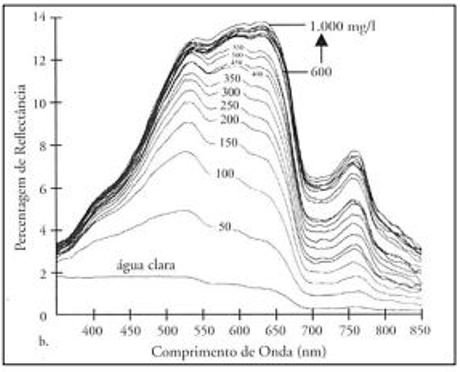
Segundo Novo (2010), corpos hídricos que apresentam partículas inorgânicas em suspensão (sólidos dissolvidos e em suspensão na água) tendem a apresentar curvas de comportamento espectral superiores à da água pura. Dessa forma, quanto maior a concentração de sedimentos em suspensão na água, maior será sua reflectância, tendo em vista que esses componentes aumentam o coeficiente de espalhamento do volume de água.
A Figura 1 ilustra a reflectância espectral da água clara pura e da água contendo diversas concentrações de sólidos em suspensão.
Figura 1: Resposta espectral da água contendo sólidos em suspensão
2.3 GOOGLE ENGINE EARTH
O Google Earth Engine (GEE) é um serviço de processamento que possibilita realizar o processamento geoespacial em escala, com a tecnologia do Google Cloud Platform Bem-vindo, (2021) (GEE, 2021). Basicamente, o objetivo do GEE é fornecer uma plataforma interativa para o desenvolvimento de algoritmos geoespaciais em escala, viabilizar a ciência de alto impacto orientada por dados e viabilizar o tratamento de informações envolvam grandes conjuntos de dados geoespaciais.
O GEE permite que os usuários executem algoritmos em imagens e vetores georreferenciados armazenados na infraestrutura do Google Comece (GEE, 2021). A API (Application Programming Interface) do GEE fornece uma biblioteca de funções que podem ser aplicadas aos dados para exibição e análise. O catálogo de dados públicos disponibilizado contém uma grande quantidade de imagens públicas e conjuntos de dados vetoriais. Os ativos privados também podem ser criados nas pastas pessoais dos usuários. O GEE e disponibiliza as linguagens de programação JavaScript e Python.
2.4 MACHINE LEARNING
O aprendizado de máquina, ou machine learning, é um campo do conhecimento dentro da área de Inteligência Artificial, e se refere à capacidade de obtenção de informações e determinação de padrões a partir de um conjunto de dados (GOODFELLOW; BENGIO; COURVILLE, 2016). A partir dessa característica, surge a possibilidade de obter soluções e modelos para problemas complexos do mundo real baseados no comportamento dos dados. Casos de aplicação podem ser encontrados nas áreas médica, agricultura, indústria, smart cities, sistemas de cibersegurança, e-commerce, monitoramento ambiental e muito mais (SARKER, 2021; SILVA et al., 2021; ROCHA et al., 2022).
O aprendizado de máquina surge a partir da seguinte questão: um computador poderia ir além de “o que sabemos como ordenar que ele execute” e aprender por conta própria como executar uma tarefa específica? Um computador poderia nos surpreender? Em vez de programadores criarem regras de processamento de dados manualmente, um computador poderia aprender automaticamente essas regras observando os dados?
Essa questão abre as portas para um novo paradigma de programação. Na programação clássica, o paradigma da inteligência artificial simbólica, os humanos inserem regras (um programa) e dados a serem processados de acordo com essas regras e obtêm respostas. Com o aprendizado de máquina, os usuários inserem dados bem como as respostas esperadas do sistema, os quais deverão definir os resultados das regras de atualização dos modelos, essas regras podem então ser aplicadas a dados desconhecidos pelo modelo de aprendizagem para produzir novas respostas, com base no processo de treinamento dos modelos.
Os algoritmos de machine learning são ferramentas baseadas em conceitos estatísticos que permitem extrair informações relevantes de correlação e de comportamento de um conjunto de dados. Alguns desses algoritmos também possuem a característica de treinamento para obtenção de predições com base em dados de entrada e podem ser classificados quanto aos tipos de abordagem supervisionada e não-supervisionada.
As etapas de treinamento de um sistema de machine learning consistem em submeter os dados de entrada, e nos casos supervisionados as marcações feitas por humanos, comumente descritas como labels, à modelos matemáticos ou algoritmos capazes de extrair padrões entre os dados, de forma que são obtidos resultados para os dados de saída e que podem ser comparados com os labels, indicando o quão distante ou próximo os dados de saída estão dos dados reais. Após uma rotina de treinamento executada adequadamente e com resultados de assertividade satisfatórios, novos dados devem ser submetidos ao modelo para testar o comportamento das saídas a partir de informações desconhecidas, a fim de testar a capacidade de generalização obtida.
Os métodos estatísticos tradicionais e o início do desenvolvimento do machine learning concentraram-se na aprendizagem com amostras de treinamento que variavam de dezenas a poucos milhares, gerando o erro de generalização que advém principalmente do erro de aproximação do resultado verdadeiro e do erro de estimativa de não ter exemplos suficiente de treinamento para limitar a variância. Nos últimos anos houve ênfase no aprendizado em larga escala em diversas áreas, sendo que nesse caso há dados para um modelo rico o suficiente, mas o custo computacional demandado torna a atividade de treinamento computacionalmente complexa e dispendiosa, então o erro de generalização está associado à uma aproximação sub-ótima (RUSSEL; NORVIG, 2009).
2.5 REGRESSÃO LINEAR
Na análise por regressão linear o objetivo principal é estabelecer uma relação, o mais próxima possível da equação de uma reta, com o intuito de gerar uma equação que relacione esses os dados de entrada à saída e que, a partir da adição de novos dados de entrada ![]() possibilite a predição dos dados de saída
possibilite a predição dos dados de saída ![]() (CHOLLET, 2018).
(CHOLLET, 2018).
A equação 1 que representa a regressão linear é dada a seguir:
onde ![]() representa o ponto inicial da reta, a inclinação da reta e as variáveis preditoras, respectivamente.
representa o ponto inicial da reta, a inclinação da reta e as variáveis preditoras, respectivamente.
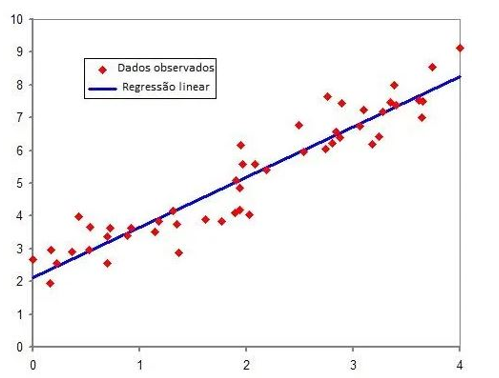
Pelo método dos mínimos quadrados, conforme a equação (2) dentre outros, obtém-se os coeficientes de modo que a linha de regressão estimada seja o mais próximo possível dos dados observados, como pode ser visto na Figura 2 (CHEIN, 2019).
sendo ![]() , os valores observados e
, os valores observados e ![]() os valores preditos.
os valores preditos.
2.6 REGRESSÃO LASSO
A regressão LASSO é um modelo linear que estima coeficientes esparsos. É útil em alguns contextos devido à sua tendência de preferir soluções com menos coeficientes diferentes de zero, reduzindo efetivamente o número de recursos dos quais a solução depende. Por esta razão, LASSO e suas variantes são fundamentais para o campo de sensoriamento comprimido. Sob certas condições, ele pode recuperar o conjunto exato de coeficientes diferentes de zero (LASSO, 2022).
Matematicamente, consiste em um modelo linear com um termo de regularização adicionado. A função objetivo a minimizar o estimador de mínimos quadrados ordinários é mostrado na equação 3:
Figura 2: Representação de dados regressão linear simples
onde X são as variáveis independentes, Y é a variável dependente, Wp são os coeficientes de ajuste do modelo de aprendizagem, N samples indica o número de amostras e alpha é a regularização dos coeficientes (W) para evitar overfitting.
2.7 MÉTRICAS ESTATÍSTICAS – ERRO ABSOLUTO MÉDIO (MAE)
Está métrica é comumente usada como função de perda para problemas de regressão e na avaliação de modelos, devido à sua interpretação muito intuitiva em termos de erro relativo, abaixo temos a fórmula, conforme a equação (4):
sendo ![]() e
e ![]() , os valores real e predito pelo modelo, respectivamente.
, os valores real e predito pelo modelo, respectivamente.
2.8 MÉTRICAS ESTATÍSTICA – COEFICIENTE DE DETERMINAÇÃO ()
Está métrica representa a proporção da variância da variável dependente ![]() que foi explicada pelas variáveis independentes no modelo. Ela fornece uma indicação da qualidade do ajuste e, portanto, uma medida de quão bem as amostras não vistas provavelmente serão previstas pelo modelo, por meio da proporção da variância explicada em (SCIKIT LEARN, 2022), conforme a equação (5):
que foi explicada pelas variáveis independentes no modelo. Ela fornece uma indicação da qualidade do ajuste e, portanto, uma medida de quão bem as amostras não vistas provavelmente serão previstas pelo modelo, por meio da proporção da variância explicada em (SCIKIT LEARN, 2022), conforme a equação (5):
onde ym é a média aritmética dos dados valores reais.
3. METODOLOGIA
Esta seção descreve a metodologia proposta para o desenvolvimento deste trabalho, onde o objetivo é descreve e implementar a metodologia proposta.
Para o modelo de predição da turbidez, foram utilizadas, como variáveis independentes, as bandas 2, 3 e 4 do Satélite Landsat 8 OLI e os parâmetros limnológicos cor verdadeira e sulfato obtidos por meio de coletas de superfície e medição da turbidez da zona fótica, previamente realizadas. De forma análoga, o treinamento dos modelos de predição do parâmetro sólidos totais utilizou, como variáveis independentes, as bandas 1, 2, 4, 6 e 7 do satélite Landsat 8 OLI e os parâmetros limnológicos sulfato (coleta de superfície) e sólidos dissolvidos totais_sdt obtidos por meio de coletas de superfície, previamente realizadas.
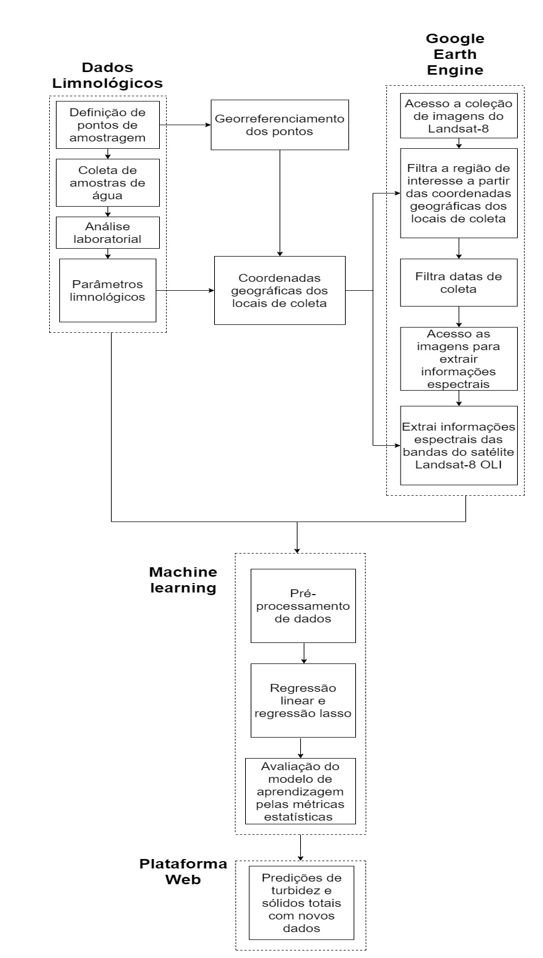
Com base na Figura 3, o bloco indicado por dados limnológicos é composto pelas etapas relativas à definição dos pontos de amostragem, coletas de amostras de água, análise laboratorial e, posteriormente, os cálculos dos valores numéricos de cada parâmetro de interesse.
Os locais das coletas de amostras de água são georreferenciados e correlacionados aos resultados das medições prévias realizadas e, então, disponibilizados à plataforma do Google Engine Earth. Nessa plataforma, após o acesso às imagens selecionadas do Satélite Landsat 8, as regiões de interesse da bacia hidrográfica são identificadas com base nas coordenadas geográficas e extraídas as informações espectrais das bandas da imagem que deverão ser aplicadas no treinamento dos modelos.
O bloco Google Earth Engine tem por finalidade, após o acesso à coleção de imagens do satélite Landsat-8 OLI, segmentar a região de interesse da bacia hidrográfica sob análise, extrair as datas das imagens coincidentes ou próximas das datas de coletas dos dados limnológicos e submeter essas imagens à etapa de pré-processamento. Dentre essas, a etapa de correção atmosférica é de grande importância para estudos hídricos em reservatórios.
As informações espectrais extraídas da plataforma do GEE, são adicionadas ao bloco machine learning, onde serão tratados na etapa de pré-processamento, onde nessa etapa é feito toda a preparação dos dados, para que os mesmos possam ser apresentados as técnicas regressão, para fazer o treinamento do modelo de aprendizagem e posteriormente usar esse modelo treinado para fazer novas predições de parâmetros limnológicos totais na plataforma Web.
Após a aprendizagem e validação dos modelos com base nas métricas estatísticas, esses modelos são incorporados à Plataforma web que possibilitará, a usuários não especialistas, realizar a predição dos parâmetros limnológicos, usando informações espectrais do Landsat 8 OLI.
Figura 3: Diagrama de blocos da metodologia proposta
O bloco plataforma Web é uma aplicação onde os modelos de regressão, previamente treinados, podem ser usados para a realização de novas predições através de novos dados informados pelo usuário. A plataforma implementada, ilustrada na Figura 4, está disponível em http://plattform.herokuapp.com/.
3.1 BASE DE DADOS
A base de dados utilizada tem um total de 97 amostras dos dados limnológicos de interesse, do qual 70% foram utilizados para a etapa de treinamento dos modelos de regressão e 30% para a etapa de teste. A validação do modelo na etapa de treinamento foi realizada utilizando-se o coeficiente de determinação e a avaliação dos testes foi feita por meio das métricas, erro absoluto médio e erro percentual absoluto médio.
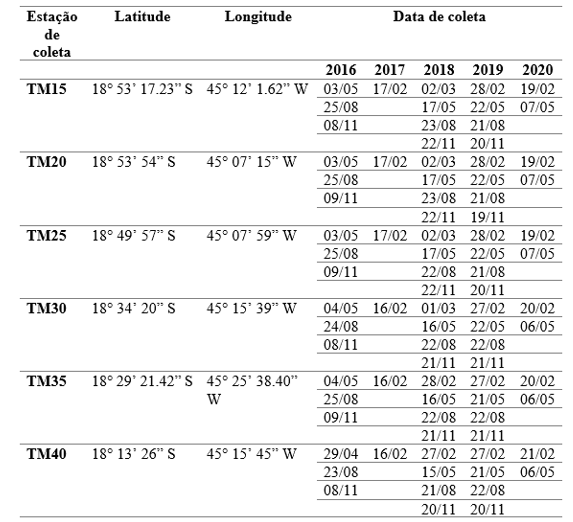
A Tabela I mostra as informações relacionadas à coleta de dados limnológicos no reservatório de Três Marias/MG, disponibilizados pela CEMIG e utilizados neste trabalho.
Tabela 1: Coordenadas geográficas dos pontos de coleta e respectivas datas no reservatório de Três Marias/MG
3.2 ESTUDO DE CASO: REPRESA DE TRÊS MARIAS – MG
Com base nos dados relativos à Represa de três Marias, localizada em Minas Gerais – Brasil, disponibilizados pela CEMIG, nesta seção serão apresentados os resultados obtidos pelos modelos de regressão, nas fases de treinamento e testes, em relação à predição dos parâmetros limnológicos turbidez e sólidos totais.
Serão mostrados os resultados do coeficiente de determinação, usado para a validação dos modelos nas etapas de treinamento, e das métricas estatísticas erro absoluto médio e erro percentual absoluto médio para avaliação dos desempenhos dos modelos nas etapas de testes, após o processo de aprendizagem. Serão também apresentados os gráficos de resíduos que permitem visualizar a aproximação entre os valores reais dos parâmetros sólidos totais e turbidez e os valores preditos, obtidos por meio da Plataforma web.
Figura 4: Visão geral da plataforma Web Análise da Qualidade da Água – Represa de Três Marias – MG

3.3 RESULTADOS E DISCUSSÃO
A seguir, serão apresentados os resultados do coeficiente de determinação, conforme a Tabela 2, usados para a validação dos modelos na etapa de treinamento, e os resultados obtidos em relação às métricas estatísticas, erro absoluto médio e erro percentual absoluto médio, indicados na Tabela 3, sobre a avaliação do desempenho dos modelos nas etapas de testes, após o processo de treinamento do modelo de aprendizagem.
Serão também apresentados os gráficos de resíduos que permitem visualizar a aproximação entre os valores reais dos parâmetros sólidos totais e turbidez e os valores preditos, que foram obtidos a partir da plataforma web do Reservatório Três Marias – MG – Brasil, (http://plattform.herokuapp.com/).
De acordo com a Tabela II, pode-se observar que, após a fase de treinamento, o modelo de regressão linear apresentou uma melhor aproximação entre os valores preditos e os valores reais, em relação à regressão LASSO, para ambos os parâmetros limnológicos turbidez e sólidos totais, com diferenças em torno de 0.154 e 0.014, respectivamente.
Segundo os resultados da Tabela III, o erro absoluto médio e o erro percentual absoluto médio apresentado pelo modelo de regressão linear indicam um desempenho pior que a técnica regressão LASSO para a predição de sólidos totais e turbidez.
Há uma diferença grande entre os valores encontrados nas métricas estatísticas para o parâmetro turbidez e sólidos totais, essa diferença tem vários motivos, dentre eles, alguma possível dependência entre as variáveis regressoras e sua correlação com a variável de saída.
Tabela 2. Resultados dos coeficientes de determinação para os modelos de regressão linear e LASSO
| Tipo de Modelo | Quantidade de dados utilizada treinamento | Parâmetro | Coeficiente de Determinação |
| Regressão Linear | 67
|
Turbidez | 0.7213 |
| Sólidos Totais | 0.832 | ||
| Regressão LASSO | 67 | Turbidez | 0.567 |
| Sólidos Totais | 0.818 |
Fonte: (Próprio Autor).
Tabela 3. Resultados do erro absoluto médio e erro percentual absoluto médio para os modelos de regressão linear e LASSO.
| Tipo de Modelo | Quantidade de dados utilizada teste | Parâmetro | Erro absoluto médio | Erro percentual absoluto médio (%) |
| Regressão Linear | 30 | Turbidez | 2.511 | 2.152 |
| Sólidos Totais | 4.822 | 0.090 | ||
| Regressão LASSO | 30 | Turbidez | 1.938 | 1.368 |
| Sólidos Totais | 4.636 | 0.087 |
Fonte: (Próprio Autor).
Essas condições variam para cada parâmetro limnológico, ou seja, alguns parâmetros podem estar mais correlacionados que outros e isso influencia diretamente na predição de novos parâmetros. Além disso, a base de dados é composta por uma quantidade insuficiente de informações, o que compromete o desempenho dos modelos.
As figuras 5 a 8 mostram os gráficos de resíduos onde é possível visualizar as diferenças entre os valores reais e os valores preditos pelos modelos, para as fases de treinamento e teste. Assim, quanto mais próximos os resíduos estiverem do eixo há a indicação de que os valores preditos pelo modelo estão mais próximos dos valores reais.
Figura 5: Gráfico de resíduos sólidos totais usando a regressão linear
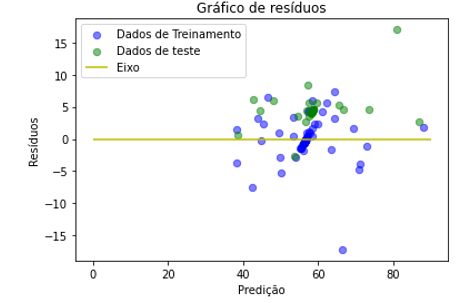
Figura 6: Gráfico de resíduos turbidez usando a regressão linear
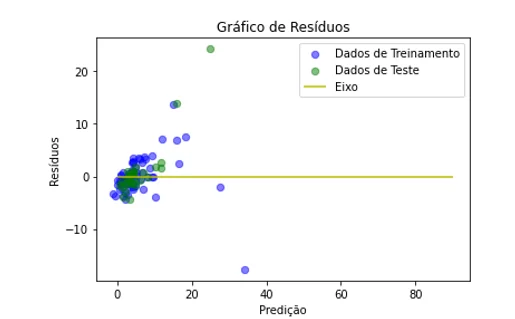
As figuras 5 e 6 apresentam os resíduos relativos à predição dos parâmetros sólidos totais e turbidez, respectivamente, obtidos pelo modelo de regressão linear. Observando-se os gráficos que destacam as regiões de maior número de ocorrência, pode-se ver que o modelo de aprendizagem conseguiu fazer as predições nos dados de teste a partir dos dados de treinamento, de tal modo que chegou mais próximo dos valores reais, indicando que o modelo de aprendizagem pode ser generalizável.
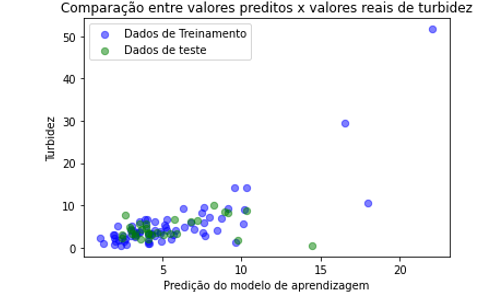
As figuras 7 e 8 apresentam os resíduos relativos à predição do parâmetro turbidez, obtidos pelo modelo de regressão LASSO. Observando-se os gráficos que destacam as regiões de maior número de ocorrência, pode-se ver que o modelo de aprendizagem conseguiu fazer as predições tanto com os dados de treinamento e de teste, indicando a validez do modelo de aprendizagem proposto e da plataforma Web desenvolvida para predições de parâmetros limnológicos, apesar da quantidade insuficiente de dados disponíveis no banco de dados.
Figura 7: Gráfico de resíduos sólidos totais usando a regressão LASSO
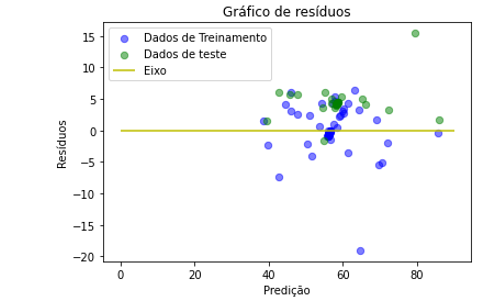
Figura 8: Gráfico de resíduos turbidez usando a regressão LASSO
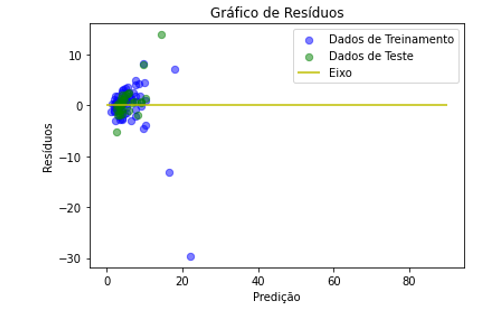
Figura 9: Valores preditos x Valores reais sólidos totais usando regressão linear
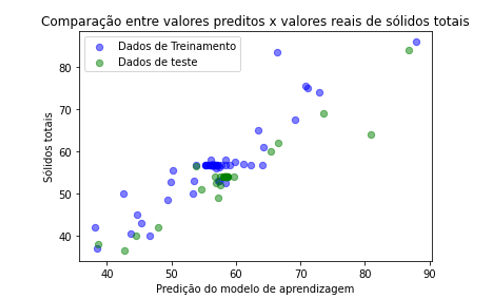
As figuras 9 a 12 mostram a comparação entre os valores preditos pelo modelo de aprendizagem e valores reais dos parâmetros sólidos totais e turbidez.
Figura 10: Valores preditos x Valores reais sólidos totais usando a regressão LASSO
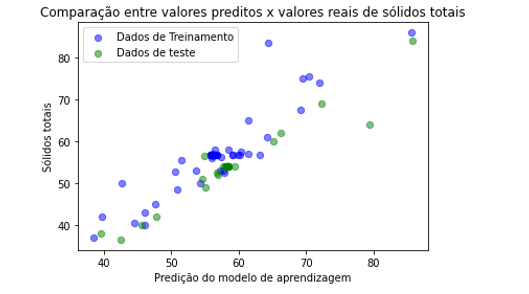
Figura 11: Valores preditos x Valores reais para a turbidez usando regressão linear
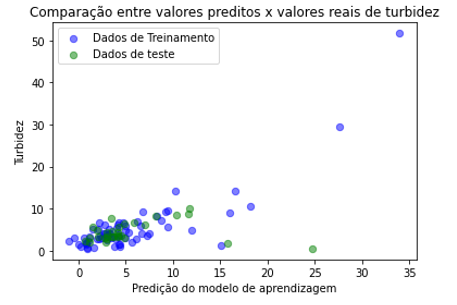
Figura 12: Valores preditos x Valores reais turbidez usando regressão LASSO
Em Marinho et al. (2021) foi feito o monitoramento do parâmetro limnológico sólidos suspensos (SSC) no Rio Negro, na bacia amazônica, os resultados obtidos coeficiente de determinação de 0,86 e um erro menor que 30% nos de predição treinados. Em Lobo et al. (2021), os resultados obtidos pelo modelo final indicam um coeficiente de determinação de 0,86 e um erro percentual médio absoluto (MAPE) próximo de 90% para predição do índice de estado trófico (TSI). O trabalho desenvolvido por Zhu e Mao (2021) tem como objetivo fazer predição do índice de estado trófico (TSI) em águas urbanas, o estudo foi desenvolvido na cidade de Gongqingcheng na China, os resultados obtidos foram coeficiente de determinação de 0,922, erro médio quadrático (RMSE) de 3,256, erro percentual médio absoluto (MAPE) de 2,494%.
Observando-se os resultados dos trabalhos citados no parágrafo anterior e os resultados apresentados neste trabalho, conforme as tabelas II e III, pode-se afirmar que a metodologia proposta é válida, e que poderá ser estendida a outros parâmetros desde que uma base de dados mais ampla esteja disponível. O desempenho satisfatório já obtido em relação às predições realizadas reforçam a aplicação do sensoriamento remoto e o uso técnicas de machine learning para o monitoramento da qualidade da água em reservatórios hídricos, em geral.
4. CONCLUSÃO
O principal objetivo deste trabalho tratou da proposição de uma metodologia capaz de fornecer a predição de parâmetros da qualidade da água em reservatórios hídricos de água doce. Para efeitos de validação, a metodologia proposta foi aplicada em um estudo de caso no Reservatório de Três Marias/MG.
Este trabalho também apresenta o desenvolvimento de uma plataforma web onde a predição dos parâmetros limnológicos pode ser realizada a partir de informações espectrais das bandas do satélite Landsat 8 OLI e medições prévias de parâmetros limnológicos, já disponíveis em séries históricas.
Os modelos de predição escolhidos baseiam-se nas técnicas de regressão linear e de LASSO e, como pôde-se observar na seção de resultados e discussões, o modelo treinado com a técnica de regressão linear obteve melhores resultados em relação ao coeficiente de determinação. Assim, o modelo de regressão linear também apresentou um melhor desempenho, comparado ao modelo por regressão LASSO, na fase de testes.
Uma limitação do trabalho pode ser constatada em relação à reduzida quantidade de informações da base de dados. Novas propostas, envolvendo técnicas mais avançadas de machine learning, poderão ser desenvolvidas desde que superadas essas restrições quanto à quantidade e diversidade dos dados.
REFERÊNCIAS
AGÊNCIA NACIONAL DAS ÁGUAS (ANA). Agência nacional de águas e saneamento básico. Disponível em: https://www.ana.gov.br/. Acesso em: 29/05/2019.
ALDHYANI, Theyazn H. H.; AL-YAARI, Mohammed; ALKAHTANI, Hasan; MAASHI, Mashael. Water Quality Prediction Using Artificial Intelligence Algorithms. Applied Bionics and Biomechanics. Londres, 2020, v. 2020, Disponível em: https://doi.org/10.1155/2020/6659314. Publicado em: 30/12/2020.
BATUR, Ersan; MAKTAV, Derya. Assessment of Surface Water Quality by Using Satellite Images Fusion Based on PCA Method in the Lake Gala. IEEE Transactions on Geoscience and Remote Sensing. Turquia, 2018, v. 57, n. 5, p. 2983 – 2989. Disponível em: https://doi.org/10.1109/TGRS.2018.2879024. Acesso em: 29/07/2019.
GOOGLE ENGINE EARTH (GEE). Bem-vindo ao google earth engine. Disponível em: https://developers. google.com/earth-engine/. Acesso em: 12/04/2021.
GOOGLE ENGINE EARTH (GEE). Comece a usar o earth engine. Disponível em: https://developers.google. com/earth-engine/guides/getstarted. Acesso em: 12/04/2021.
CHEIN, Flávia. Introdução aos modelos de regressão linear: um passo inicial para compreensão da econometria como uma ferramenta de avaliação de políticas públicas, Enap, Brasília, 2019. ISBN: 978-85-256-0115-5. Disponível em: https://repositorio.enap.gov.br/bitstream/1/4788/1/Livro_Regress%C3%A3o%20Linear.pdf. Acesso em: 09/07/2019.
CHOLLET, François. Deep Learning with Python, 1 ed. Manning Publications Co, Estados Unidos da América, 2018. ISBN: 9781617294433.
GOODFELLOW, Ian; BENGIO, Yoshua; COURVILLE, Aaron. Deep Learning. The MIT Press, Estados Unidos da América, 2016.
JENSEN, John J. Sensoriamento Remoto do Ambiente: Uma Perspectiva em recursos Terrestres, 4 ed. Blucher, São Paulo, 2010. ISBN 978-8521205401.
LOBO, Felipe de Lucia; Nagel, Gustavo Willy; MACIEL, Daniel Andrade; CARVALHO, Lino Augusto Sander de; MARTINS, Vitor Souza; BARBOSA, Cláudio Clemente Faria; NOVO, Evlyn Márcia Leão de Moraes. AlgaeMAp: Algae Bloom Monitoring Application for Inland Waters in Latin America. Remote Sensing. 2021, v. 13, n. 15 (2874). https://doi.org/10.3390/rs13152874. Publicado em: 22/07/2021.
MARINHO, Rogério Ribeiro; HARMEL, Tristan; MARTINEZ, Jean-Michel; JUNIOR, Naziano Pantoja Filizola. Spatiotemporal Dynamics of Suspended Sediments in the Negro River, Amazon Basin, from In Situ and Sentinel-2 Remote Sensing Data. ISPRS International Journal of Geo-Information. 2021, v. 10, n. 2 (86). Disponível em: https://doi.org/10.3390/ijgi10020086. Publicado em: 19/02/2021.
MOTA, Myriam Becho; BRAICK, Patrícia Ramos. História das cavernas ao terceiro milênio: programa completo de: pré-história e de história antiga, medieval, moderna, contemporânea, da América e do Brasil, 2 ed. Editora Moderna, São Paulo 2002. ISBN 851603372.
NOVO, Evlyn. M. L. de Moraes. Sensoriamento Remoto: Princípios e Aplicações, 4 ed. Blucher, São Paulo, 2010. ISBN: 9788521205401.
QI, Chuhan; HUANG, Shuo; WANG, Xiaofei. Monitoring Water Quality Parameters of Taihu Lake Based on Remote Sensing Images and LSTM-RNN. IEEE Access. 2020, v. 8, p. 188068-188081. Disponível em: https://doi.org/10.1109/ACCESS.2020.3030878. Publicado em: 14/10/2020.
RUSSELL, Stuart; NORVIG, Peter. Artificial Intelligence: A Modern Approach. 3 ed. Prentice Hall Press, Estados Unidos da América, 2009.
ROCHA, Douglas Abreu da; FERREIRA, Flávia Magalhães Freitas; PEIXOTO, Zélia Myriam Assis. Diabetic retinopathy classification using VGG16 neural network. Research on Biomedical Engineering. Brasil, 2022, v.38, p. 761 – 772. Disponível em: https://doi.org/10.1007/s42600-022-00200-8. Publicado em: 02/02/2022.
SILVA, Maycon. G. G; SILVA, Daiane. J.; COSTA, Paloma. D.; SILVA, Rafaela C.; CASSIMIRO, Tanízia. E. B., AMORIM, Luciana. S.; ROCHA, Douglas. A.; PEIXOTO, Zélia. M. A. Análise da qualidade da água em escala de bacia hidrográfica utilizando imagens de satélite, matrizes de coocorrência e classificador de Bayes. Water Supply. 2021, v. 21, n. 8, p. 4418–4428. Disponível em: https://doi.org/10.2166/ws.2021.192. Publicado em: 22/06/2021.
SCIKIT LEARN. Regressão LASSO. Disponível em: https://scikit-learn.org/stable/modules/linear_model.html#lasso. Acesso em 08-02-2022.
SCIKIT LEARN. Coeficiente de determinação: Disponível em: https://scikit-learn/org/stable/modules/model evaluation.html#regression-metrics. Acesso em: 09/02/2022.
SARKER, Iqbal H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Computer Science. 2021, v. 2, n. 160 (2021). Disponível em: https://doi.org/10.1007/s42979-021-00592-x. Publicado em: 22/03/2021.
SIT, Muhammed; DEMIRAY, Bekir Z; XIANG, Zhongrun; EWING, Gregory J; SERMET, Yusuf; DEMIR, Ibrahim. A comprehensive review of deep learning applications in hydrology and water resources. Water Science & Technology. 2020, v. 82, n. 12, p. 2635 – 2670. Disponível em: https://doi.org/10.2166/wst.2020.369. Publicado em: 05/08/2020.
TUNDISI, José Galizia; TUNDISI, Takako Matsumura. Limnologia, 1 ed. Oficina de Textos, São Paulo, 2008. ISBN: 978-85-86238-66-6.
VILELA, Marcos Augusto Macedo Araújo. Metodologia para monitoramento da qualidade da água de reservatórios utilizando sensoriamento remoto. Dissertação (Mestrado em Engenharia Civil) – Faculdade de Engenharia Civil, Universidade Federal de Uberlândia, 2010.
ZHU, Shijie; MAO, Jingqiao. A machine learning approach for estimating the trophic state of urban waters based on remote sensing and environmental factors. Remote Sensing. 2021, v. 13, n. 13 (2498). ISSN 2072-4292. Disponível em: https://doi.org/10.3390/rs13132498, Publicado em: 26/06/2021.
[1] Mestre em Engenharia Elétrica, Bacharel em Engenharia Eletrônica. ORCID: 0000-0001-8384-9525.
[2] Mestre em Engenharia Elétrica, Bacharel em Engenharia Eletrônica. ORCID: 0000-0003-1442-9038.
[3] Orientadora. Doutorado em Engenharia Elétrica (UFMG), Mestrado em Engenharia Elétrica (UFMG), Bacharelado em Engenharia Eletrônica e de Telecomunicação (PUC Minas). ORCID: 0000-0002-1493-2875.
Enviado: Setembro, 2022.
Aprovado: Dezembro, 2022.