ARTIGO ORIGINAL
SANTOS, Hádrian George da Rocha [1], CHAVES, Alexandre Ribeiro [2]
SANTOS, Hádrian George da Rocha. CHAVES, Alexandre Ribeiro. Análise estrutural por elementos finitos do chassi de um veículo Baja SAE. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 06, Ed. 12, Vol. 10, pp. 153-180. Dezembro de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-mecanica/veiculo-baja-sae, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-mecanica/veiculo-baja-sae
RESUMO
O Programa Baja SAE constitui-se de um projeto de abrangência internacional que promove competições estudantis para o desenvolvimento de veículos off-road capazes de operar em terrenos acidentados com pedras, lama e tronco de árvores. Nesse sentido, o chassi spaceframe deve ser projetado para suportar os pesos do piloto e dos subsistemas de transmissão e suspensão, além de resistir aos esforços provenientes de colisões e de obstáculos presentes nas provas dinâmicas. Dessa forma, as equipes devem utilizar em seu projeto um motor padrão de 4 tempos e de potência 10 hp, tendo em vista que o peso final do protótipo influencia diretamente na performance e integridade física do piloto. Sendo assim, o aperfeiçoamento da gaiola aumenta a competividade das equipes. Neste trabalho, o presente artigo objetiva avaliar o comportamento estrutural do protótipo 2020-2021 da equipe Serbaja UFS por meio de simulações computacionais pelo Método dos Elementos Finitos, verificando a integridade da estrutura do chassi quando submetido a diferentes impactos e vibrações. Com base nas velocidades de operação e nas solicitações externas, foi realizada uma análise estática linear do chassi para avaliar as tensões e deformações, bem como uma análise modal para identificar as frequências naturais e os modos de vibrar do chassi, evitando o fenômeno de ressonância em razão da frequência do motor ou de esforços de natureza harmônica provocados por obstáculos. A metodologia das análises estruturais se baseia na definição das restrições e dos carregamentos aplicados ao chassi em colisões frontais e laterais, capotamentos e cenários de torção. Para tal, as cargas calculadas permitem avaliar as tensões máximas pelo critério de falha de von Mises, verificando o comportamento mecânico da estrutura em zonas de concentração de tensão. Os resultados apontam que a estrutura do chassi sofre deformações menores que os limites estabelecidos pelo regulamento Baja SAE e permanece no regime elástico em cenários críticos, com coeficiente de segurança mínimo de 1,2. Portanto, a gaiola analisada cumpre com os requisitos de projeto e é capaz de suportar, com segurança, os esforços transmitidos.
Palavras-chave: Baja SAE, Chassi, Elementos Finitos, Análise Estrutural.
1. INTRODUÇÃO
O programa Baja SAE foi criado na década de 1970 pela Sociedade de Engenheiros Automotivos (Society of Automotive Engineers – SAE) para estimular estudantes de Engenharia a projetar, construir e testar um veículo off-road capaz de superar vários tipos de terrenos acidentados e obstáculos em competições com outras equipes estudantis vinculadas a instituições de ensino superior (DANTAS, 2019).
Nesse sentido, a necessidade de desenvolver um veículo seguro e eficiente incentiva os estudantes a utilizarem os conhecimentos teóricos obtidos em sala de aula em contextos práticos. Assim, os participantes experimentam momentos de âmbito profissional, tais como o trabalho em equipe, montagem, administração e marketing.
Nessa perspectiva, a fim de participar do Programa Baja SAE Brasil, formou-se, em 2009, a equipe Serbaja, a qual é vinculada ao Departamento de Engenharia Mecânica da Universidade Federal de Sergipe (UFS). Nesse bojo, a equipe busca desenvolver um veículo monoposto, confiável, ergonômico e apto a suportar esforços em vários tipos de terrenos.
A competição Baja SAE ocorre em terrenos acidentados e com vários obstáculos, tais como lamas, troncos e aclives. Ademais, durante a competição, colisões entre os veículos e com os obstáculos são recorrentes. Todavia, o regulamento da competição determina que, caso o veículo tenha sua estrutura danificada durante as provas dinâmicas e for julgado como não seguro, ele deve ser reparado antes de retornar à competição.
Por isso, é importante que a estrutura do veículo seja robusta e rígida o suficiente para resistir aos esforços sem comprometer o funcionamento do veículo, evitando, assim, o desenvolvimento de deformações plásticas em razão de capotamentos e colisões frontais, traseiras e laterais.
Dessa forma, o objeto de estudo deste trabalho é o chassi do veículo, uma vez que se trata do principal componente estrutural, tendo em vista que deve sustentar os subsistemas e os seus componentes, como motor, transmissão e suspensão, além de ser ergonômico e preservar a vida do piloto em casos de acidentes.
Dessa forma, considera-se vários parâmetros estabelecidos pelo programa Baja SAE para o desenvolvimento do trabalho, haja vista que o design do chassi deve seguir padrões e regras de segurança estabelecidas pelos organizadores, por isso, o chassi analisado neste estudo segue as conformidades do regulamento da competição.
Sendo assim, com base nos requisitos impostos no regulamento da competição, o desenvolvimento de um estudo com foco na análise estrutural do chassi apresenta grande relevância, considerando que a gaiola é responsável por uma parcela significativa do peso do veículo e é o principal meio de absorção de energia em casos de impacto. Além disso, a análise estrutural permite a identificação de falhas e concentrações de tensões antes da fabricação do protótipo, contribuindo para uma redução de custos e do tempo de desenvolvimento.
Portanto, objetiva-se avaliar o comportamento estrutural do protótipo 2020-2021 da equipe Serbaja UFS por meio de simulações computacionais pelo Método dos Elementos Finitos, verificando a integridade da estrutura do chassi quando submetido a diferentes impactos e vibrações
2. METODOLOGIA
A primeira etapa do projeto é a modelagem 3D da estrutura da gaiola utilizando o software SolidWorks 2021 licenciado para a equipe Serbaja. Nessa fase, é realizado o estudo do Regulamento Baja SAE para que o chassi cumpra com as restrições geométricas e estruturais exigidas. Em seguida, os componentes que não exercem funções estruturais de grande importância são removidos da geometria no software SpaceClaim vinculado ao ANSYS Workbench, a fim de reduzir o tempo de processamento nas simulações computacionais.
Após o reconhecimento do modelo CAD no software de elementos finitos, são criados os elementos de viga com base nos perfis dos tubos primários e secundários do chassi para uma posterior geração de malha e execução das simulações no módulo Estrutural e Modal do software ANSYS.
A metodologia utilizada para a análise do chassi do veículo é apresentada na Figura 1, que mostra os principais passos realizados no processo de desenvolvimento da análise.
Figura 1 – Fluxograma das etapas de análise.
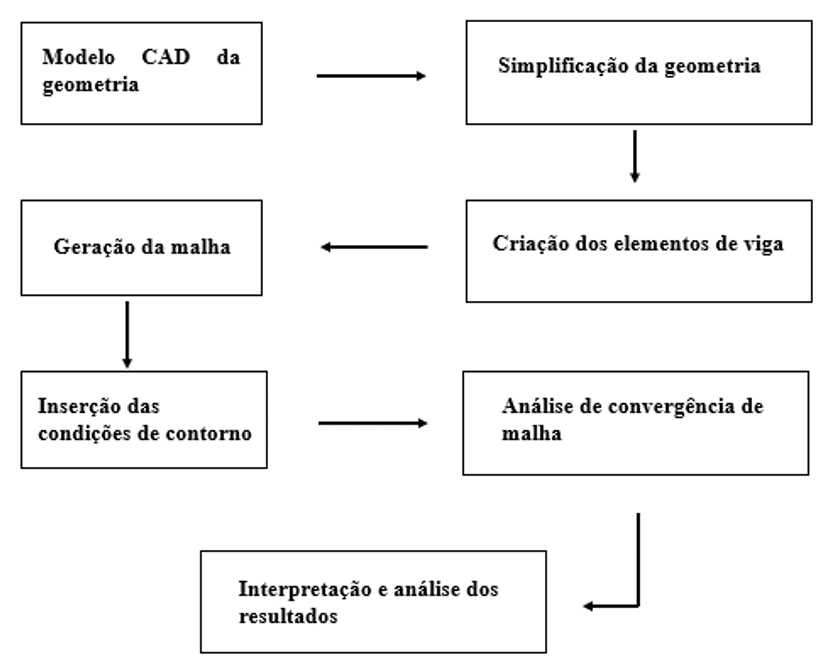
Em suma, a metodologia se divide em três etapas: a de pré-processamento, que abrange o desenvolvimento da geometria até a definição e inserção das condições de contorno. A etapa de processamento corresponde aos cálculos nodais realizados pelo software CAE. Por fim, a etapa de pós-processamento, consiste na análise dos resultados, ou seja, na avaliação das tensões, deformações e frequências, sendo necessário identificar a coerência dos dados.
3. FUNDAMENTAÇÃO TEÓRICA
3.1 RIGIDEZ À FLEXÃO
Segundo Gillespie (1992), quando um veículo transpõe ondulações ou obstáculos na pavimentação que provocam uma translação do conjunto de suspensão traseiro de forma desigual do conjunto traseiro, o veículo é submetido a um momento fletor ao longo do eixo longitudinal da estrutura, como apresentado na Figura 2.
Figura 2 – Esforços devido a translação do conjunto de suspensão dianteiro.
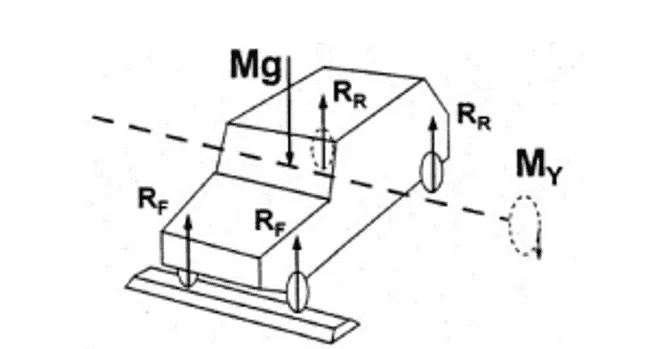
Nesse sentido, a rigidez flexional, ou rigidez à flexão, corresponde à capacidade do chassi de suportar o tipo de solicitação apresentado na Figura 2. Assim, é necessário que a estrutura do veículo seja dimensionada para suportar esforços oriundos de situações diversas, tais como lombadas e buracos trepidações), além de resistir aos esforços verticais aplicados nos elementos de suspensão.
3.2 RIGIDEZ À TORÇÃO
De acordo com Gillespie (1992), quando um veículo transpõe ondulações ou obstáculos na pavimentação que provocam uma translação em apenas uma das rodas, o veículo é submetido a um momento fletor e a um momento torsor ao longo do eixo longitudinal da estrutura, como apresentado na Figura 3.
Figura 3 – Esforços devido a translação da roda dianteira direita.
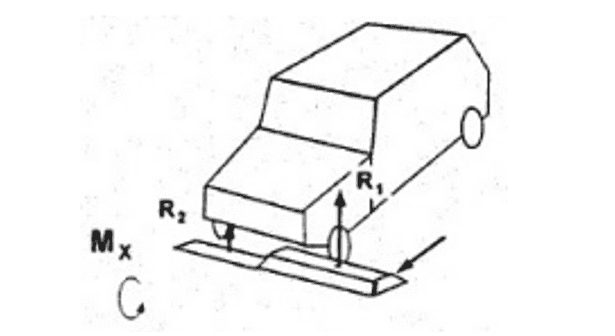
Nesse bojo, a rigidez torcional, ou rigidez à torção, corresponde à capacidade do chassi de suportar o tipo de solicitação apresentado na Figura 3. Outrossim, por ser resultado de uma combinação de carregamentos, esse esforço pode causar grandes deformações na estrutura, por isso deve ser analisado criteriosamente.
3.3 CHASSI SPACEFRAME
Em geral, um chassi eficiente precisa suportar o peso total do veículo e fornecer segurança ao piloto nos diversos casos de impacto. Além disso, deve ter grande rigidez à torção e à flexão de modo a resistir, com uma mínima deformação, aos esforços transmitidos pelo sistema de transmissão, pela suspensão, pela travagem e pela aceleração do veículo.
Nos veículos Baja, o chassi utilizado é do tipo spaceframe, o qual é composto por tubos dispostos em formatos triangulares ou treliças. Conforme Happian-Smith (2001), o uso da triangulação em três dimensões aumenta a rigidez e a resistência à flexão e à torção do chassi quando submetido a vários tipos de carregamentos.
Além disso, a disposição em treliças promove uma distribuição homogênea dos esforços, o que contribui para reduzir o peso total da estrutura, e facilita o processo de fabricação e manutenção. Logo, o chassi spaceframe apresenta grande eficiência num contexto de produção limitada.
3.4 MÉTODO DOS ELEMENTOS FINITOS
O Método dos Elementos Finitos (MEF) é um procedimento numérico muito utilizado nos mais variados campos da Engenharia. Na Engenharia Mecânica, o método contribui para o projeto e dimensionamento de estruturas a partir da análise de deslocamentos e tensões em componentes veiculares, pórticos, pontes, dentre outros.
Consoante Furtado (2013), o Método dos Elementos Finitos se baseia na discretização e na subdivisão do domínio de um objeto em pequenas partes, denominadas de elementos. Assim, um modelo matemático pode ser simplificado em um conjunto de equações diferenciais que determinam o comportamento da estrutura a ser analisada.
Em geral, a precisão dos resultados obtidos pelo MEF está diretamente relacionada ao número de elementos utilizados na malha, a qual é composta pelos elementos e seus pontos de ligação, denominados como nós. Por isso, é necessária uma discretização adequada para que os resultados fornecidos pelas simulações numéricas e computacionais sejam condizentes com o comportamento real da estrutura.
3.5 SOFTWARES CAD E CAE
O SolidWorks é um software CAD (Computer Aided Design – Projeto Assistido por Computador) de propriedade da Dassault Systèmes S.A. que possibilita a criação de modelos tridimensionais, sendo bastante utilizado no desenho e no dimensionamento de componentes de projetos mecânicos, como o chassi de um veículo Baja.
Por outro lado, o ANSYS Workbench é um software de simulação computacional que se enquadra no ramo de tecnologia de Engenharia assistida por computador (Computer Aided Engineering – CAE) e que apresenta uma plataforma bem interfaceada com o SolidWorks, o que facilita a importação do modelo após a modelagem e evita que alguma característica geométrica seja perdida no processo. Assim, o software auxilia na validação de projetos mecânicos por meio de análises pelo Método dos Elementos Finitos (MEF).
Neste trabalho, utilizou-se o módulo estrutural do ANSYS para a análise das tensões e das frequências naturais no chassi a partir de simulações estáticas e modais.
3.6 ANÁLISE MODAL
Em suma, a análise modal realiza a medição das respostas de uma estrutura devido a excitações em um determinado espectro de frequência, obtendo, assim, as suas frequências naturais e os modos de vibração.
Dessa forma, a análise modal é de suma importância para evitar um possível efeito de ressonância no chassi a partir do deslocamento das frequências naturais para valores em que o veículo não opera. Para tais alterações, podem ser modificadas a massa, a rigidez e a geometria da estrutura.
De acordo com Meirovitch (1986), a equação na forma matricial do problema de vibrações livres para uma análise pelo Método dos Elementos Finitos (MEF) pode ser escrita pela Equação 1, em que 
é a matriz, 
a matriz de rigidez e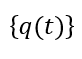 
é o vetor das coordenadas generalizadas dos graus de liberdade do modelo de elementos finitos. Ademais, 
representa o vetor aceleração das coordenadas generalizadas.
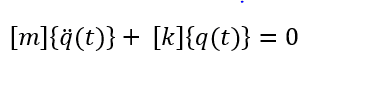(1)
No estudo de estruturas, analisar as frequências naturais de um sistema é fundamental, uma vez que, com base em Halliday et al. (2009), caso as frequências naturais das forças de excitação externas coincidam com as frequências naturais da estrutura, as oscilações resultantes podem resultar em um colapso estrutural devido ao fenômeno de ressonância, o qual pode provocar grandes deslocamentos e gerar trincas.
3.7 ANÁLISE ESTÁTICA
Além das análises modais, é fundamental analisar o comportamento da estrutura quando submetida a cargas verticais, laterais, frontais e cenários de torção em situações críticas.
Nessa análise, são verificadas as tensões aplicadas ao chassi decorrentes de carregamentos internos constantes, como o peso do motor, dos componentes da transmissão e do próprio piloto. Além disso, também podem ser analisadas as reações da estrutura a esforços externos.
Nesse aspecto, com base nas análises dos esforços e dos deslocamentos, pode-se utilizar o critério de falha de von Mises para avaliar a possibilidade de o material do chassi sofrer escoamento ou trincar por causa da ação dos carregamentos esperados, haja vista que é necessário garantir que a gaiola não falhará quando submetida às várias condições de operação de um veículo Baja (LOTTERMANN, 2014).
Neste trabalho, a análise estática utilizada é do tipo linear, na qual o material do componente em questão segue a Lei de Hooke, isto é, a deformação é diretamente proporcional à tensão.
No MEF, os elementos transmitem esforços de maneira semelhante a um conjunto de molas, o que provoca deslocamentos. Desse modo, na análise matricial de estruturas, a relação linear entre forças e deslocamentos nodais para os elementos é expressa pela Equação 2, em que 
é o vetor de carregamentos, 
é a matriz de rigidez e 
é o vetor dos deslocamentos nodais.
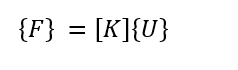(2)
4. DESENVOLVIMENTO
4.1 GAIOLA
A gaiola de proteção de um veículo Baja tem a função de prover um espaço mínimo de habitáculo ao piloto e acomodar todos os subsistemas do veículo, como o motor, a caixa de direção, o sistema de transmissão e a suspensão, sendo projetada para que não haja nenhum tipo de falha no que tange a sua integridade estrutural. Por isso, o regulamento da competição Baja SAE determina algumas medidas e angulações para os componentes do chassi, a fim de garantir uma segurança mínima para os participantes. Entre as restrições à estrutura do veículo presentes no regulamento SAE Brasil (2021), tem-se que:
- O veículo deve possuir quatro ou mais rodas não dispostas em linha reta;
- O veículo deve ser apto a acomodar um condutor de 1,45 m de altura, com peso de 42 kg até um condutor de 1,90 m de altura, com peso de 109 kg;
- A largura máxima do veículo é de 1,62 m, com as rodas direcionadas para frente, na altura estática de rodagem;
- Não há restrição para o comprimento do veículo, todavia, as provas das competições são construídas para veículos com comprimento máximo de 2,74 m;
O chassi utilizado no veículo é composto por dois tipos de membros: primários e secundários. Os elementos primários são submetidos aos maiores esforços em casos de colisões e capotamentos. Por isso, o regulamento determina que o material utilizado nos membros primários da gaiola deve ser:
- Tubo de aço circular com 25,4 mm (1 in) de diâmetro externo e 3,05 mm (0,120 in) de espessura, composto por um material com composição mínima de 0,18% de carbono;
- Perfil de aço com espessura de parede maior ou igual a 1,57 mm (0,062 in) e material de composição com conteúdo de carbono maior ou igual a 0,18%.
Por outro lado, os membros secundários possuem a função de reforço estrutural e devem ser constituídos de tubos com espessura de parede mínima de 0,89 mm, diâmetro externo ou menor dimensão externa em perfil não circular maior ou igual a 25,4 mm (1 in) e conteúdo de carbono de, pelo menos, 0,18%.
No chassi do veículo da Equipe Serbaja, toda a estrutura é composta por tubos de aço SAE 1020 (0,20% de carbono) soldados nos pontos de união, uma vez que este material é facilmente encontrado no mercado e tem uma grande gama de aplicações em elementos estruturais na indústria em geral.
Para os membros primários da estrutura do chassi, foram selecionados tubos de aço de 31,75 mm 
de diâmetro externo e 1,6 mm de espessura de parede. Para os membros secundários, foram selecionados aços tubulares de 25,4 mm (1 in) de diâmetro externo e 1,2 mm de espessura de parede.
O modelo desenvolvido é apresentado na Figura 4, sendo os membros primários identificados pela cor verde e os secundários pela cor vermelha.
Figura 4 – Modelo 3D da gaiola.
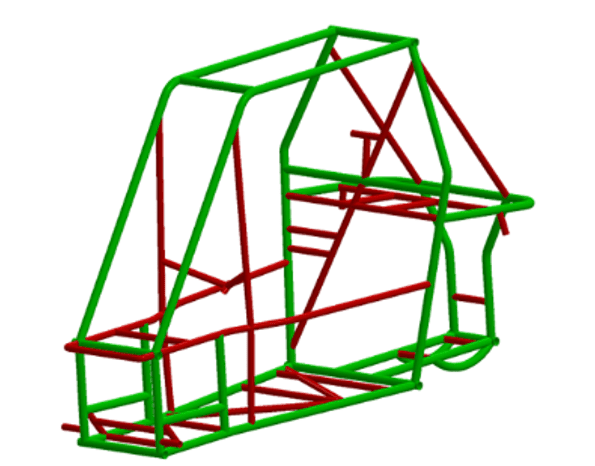
De acordo com a norma SAE Brasil (2021), para que o piloto se mantenha em segurança dentro da estrutura, os ombros, tronco, quadril, coxas, joelhos, braços, cotovelos e mãos do piloto devem ter uma folga mínima de 76 mm em relação à gaiola, enquanto deve distar pelo menos 152 mm. Nesse sentido, a fim de estudar a eficiência da gaiola, analisa-se as deformações e deflexões na estrutura nos cenários citados anteriormente. Além disso, também é necessário observar o fator de segurança para todos os carregamentos analisados.
4.2 MALHA
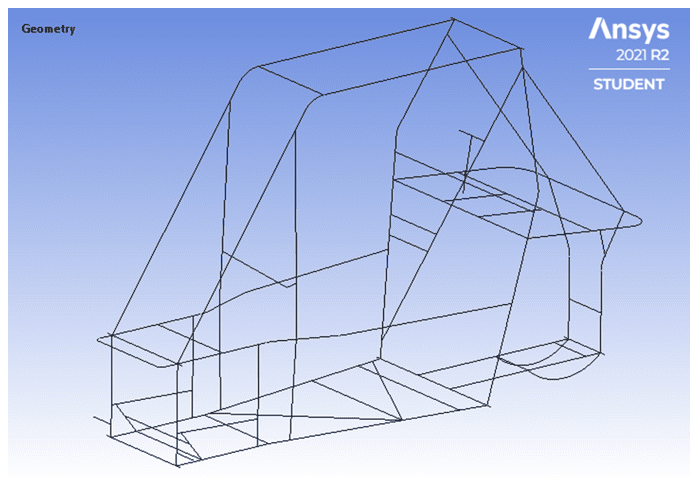
Em uma simulação estrutural com modelo tridimensional, o recurso computacional pode ser bastante elevado, demandando muito tempo para que as máquinas executem o processo. Por isso, utilizando as ferramentas do ANSYS, a estrutura da gaiola foi transformada em 2D, conforme apresenta a Figura 5.
Figura 5 – Modelo 2D da gaiola.
Portanto, utiliza-se os elementos de viga (Beams), os quais simplificam a malha e facilitam a realização dos cálculos por meio do Método dos Elementos Finitos (MEF) sem causar grandes distorções nos resultados. Logo, os componentes estruturais do chassi foram tratados como elementos de viga, uma vez que estes são eficientes no cálculo de resistência a cargas axiais, de flexão e de torção. As Figuras 6 e 7 apresentam, respectivamente, a malha gerada e os elementos de vigas utilizados.
Figura 6 – Malha gerada para as análises.
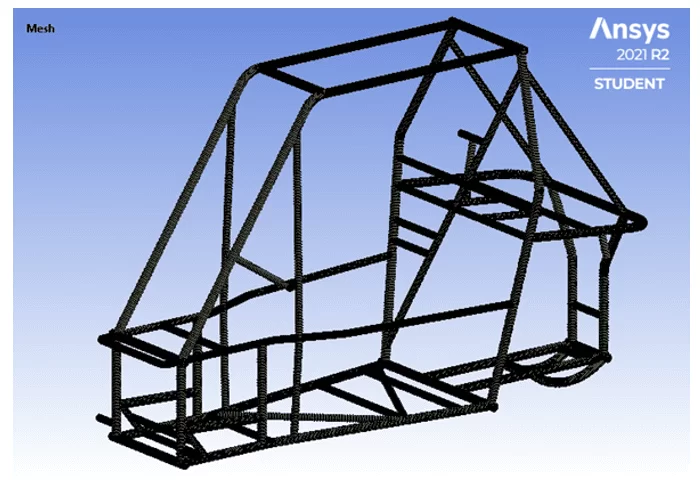
Figura 7 – Detalhes dos elementos de viga.
Neste caso, o elemento de viga utilizado é o BEAM188, o qual é formulado com base na teoria do Feixe de Timoshenko, que é uma teoria de cisalhamento de primeira ordem segundo a qual a deformação de cisalhamento transversal é constante ao longo da seção transversal, isto é, as seções transversais permanecem planas e não distorcidas após a deformação.
O BEAM188 é um elemento de viga linear, quadrático ou cúbico de dois nós em três dimensões (3D), adequado para analisar estruturas de vigas delgadas ou robustas, fornecendo opções para empenamento irrestrito e empenamento restrito de seções transversais.
Ademais, o BEAM188 tem seis ou sete graus de liberdade em cada nó, os quais incluem translações nas direções x, y e z e rotações sobre as direções x, y e z, sendo que os momentos podem ter variação linear. O elemento também inclui termos de rigidez de tensão, por padrão, em qualquer análise com grande deflexão, o que permite que os elementos analisem problemas de estabilidade flexional e torcional.
Em cada tipo de análise, realiza-se um estudo de convergência de malha. Para tal, é executado inicialmente um ensaio com uma malha não sofisticada. Em seguida, ela é refinada até que o refinamento não gere grandes alterações no resultado obtido. Assim, pode-se obter uma boa aproximação nos resultados sem refinamentos excessivos, o que reduz o tempo computacional e o custo para o desenvolvimento do projeto.
4.3 VIBRAÇÕES
No estudo de vibrações livres no chassi, o principal gerador de forças vibratórias é o motor Briggs & Stratton, 10 hp, que possui frequências naturais as quais variam entre 15 e 25 Hz (KABILAN et al., 2016). Assim, se uma das frequências naturais do chassi for próxima da frequência de excitação, a estrutura pode sofrer vibrações que causam esforços de tração, compressão, flexão ou torção, o que pode prejudicar sua integridade e reduzir o conforto do piloto sob o ponto de vista ergonômico.
Logo, a estrutura do chassi deve possuir frequência natural acima do range de operação do motor para evitar o colapso estrutural.
4.4 CONDIÇÕES DE CONTORNO
As condições de contorno correspondem às forças, restrições de movimento (engastes e juntas), pressões, temperaturas e outros dados inseridos no projeto que simulam com as condições reais às quais o projeto é submetido. Destarte, é importante que as condições confiram verossimilhança no ambiente do software para que o resultado seja condizente com uma situação real.
Anteriormente à simulação, são inseridas as propriedades do aço SAE 1020 na biblioteca de materiais do ANSYS, apresentadas na Tabela 1.
Tabela 1 – Propriedades do material dos tubos do chassi.
| Material | Aço SAE 1020 |
| Modelo constitutivo | Isotrópico linear elástico |
| Limite de escoamento | 351 MPa |
| Resistência à tração | 420 MPa |
| Módulo de elasticidade | 205 GPa |
| Coeficiente de Poisson | 0,29 |
Fonte: Autoria própria (2021).
Nesse sentido, as simulações foram realizadas no software ANSYS Workbench com a finalidade de obter as respostas da estrutura do chassi do veículo nas seguintes situações: análise modal de corpo livre e de corpo rígido; comportamento do chassi quando sujeito a colisões frontais, laterais, esforços de torção e capotamentos. Como condição de contorno, os pontos de ancoragem das bandejas de suspensão ao chassi foram tomados como fixos.
Ademais, para a validação da estrutura, utiliza-se o protocolo australiano ADR 59 (Australian Design Rule) considerando o ROPS (Roll Over Protection Structure), o qual apresenta cargas e limites máximos permitidos para deflexão em estruturas que servem de proteção ao condutor. Ademais, os níveis exigidos pelo protocolo são mais rigorosos do que os previstos no regulamento da competição Baja SAE.
Para os cálculos, estima-se um valor aproximado de 250 kg para a massa total do veículo 
, assumindo todos os elementos dos sistemas de transmissão, direção e suspensão, bem como o peso do piloto. Por fim, considera-se um valor de 
para a aceleração da gravidade 
. Ademais, seguindo a recomendação de Pawlowski (1969), utiliza-se um coeficiente de segurança de 1,8 para multiplicar o binário de forças no cenário de torção.
Logo, as intensidades de carga nos impactos laterais, frontais, verticais e no cenário de torção são especificadas na Tabela 2.
Tabela 2 – Tipos de carregamento e suas respectivas cargas.
| Tipo de carregamento | Carga |
| Torção (Binário de forças) | |
| Impacto vertical (capotamento) | |
| Impacto lateral | |
| Impacto frontal |
Fonte: Autoria própria (2021).
5. RESULTADOS
5.1 ANÁLISE MODAL DE CORPO LIVRE
Nesse tipo de análise, o chassi é considerado uma estrutura livre, de modo que nenhuma restrição de deslocamento é imposta sobre qualquer ponto do veículo, ou seja, não há limitação sobre os graus de liberdade dos elementos finitos. Essa condição de contorno simula os movimentos do chassi em uma pista de competição sem restrição de movimento ou obstáculos.
Para a análise de corpo livre, as frequências naturais da estrutura para os doze primeiros modos de vibrar são apresentadas na Tabela 3.
Tabela 3 – Doze primeiros modos de vibrar da estrutura.
| Modo de vibrar | Frequência (Hz) | Comportamento |
| 1º | 0 | – |
| 2º | 0 | – |
| 3º | 0 | – |
| 4º | 0,0019707 | – |
| 5º | 0,0036592 | – |
| 6º | 0,017579 | – |
| 7º | 42,975 | Flexão |
| 8º | 44,132 | Torção |
| 9º | 75,72 | Torção |
| 10º | 85,399 | Torção e Flexão |
| 11º | 90,973 | Torção e Flexão |
| 12º | 95,564 | Torção e Flexão |
Fonte: Autoria própria (2021).
As seis primeiras frequências são nulas ou próximas de zero. Isso significa que o software não apresentou problemas no reconhecimento da geometria da estrutura. Em relação às outras frequências, obtém-se uma faixa de 42,975 a 95,564 Hz. Nesse aspecto, o modelo resiste às oscilações causadas pelo motor que, segundo Kabilan et al. (2016), gera frequências de 15 a 25 Hz.
Analisando a vibração do chassi, verifica-se que o sétimo modo de vibração provoca esforços de flexão na estrutura e que o oitavo e o nono modo de vibrar originam deformações por torção. Além disso, os últimos modos de vibrar são resultados de uma combinação de esforços de torção e flexão.
Na Figura 8, observa-se que o sétimo modo de vibrar representa um cenário de flexão, provocando deformações na parte superior e frontal da gaiola.
Figura 8 – Comportamento de flexão no sétimo modo de vibrar.
Por outro lado, o oitavo modo de vibrar se caracteriza por ser resultado de um cenário de torção, que provoca maior deformação no tubo cruzado o qual interliga os lados direito e esquerdo da estrutura, como apresentado na Figura 9.
Figura 9 – Comportamento de torção no oitavo modo de vibrar.
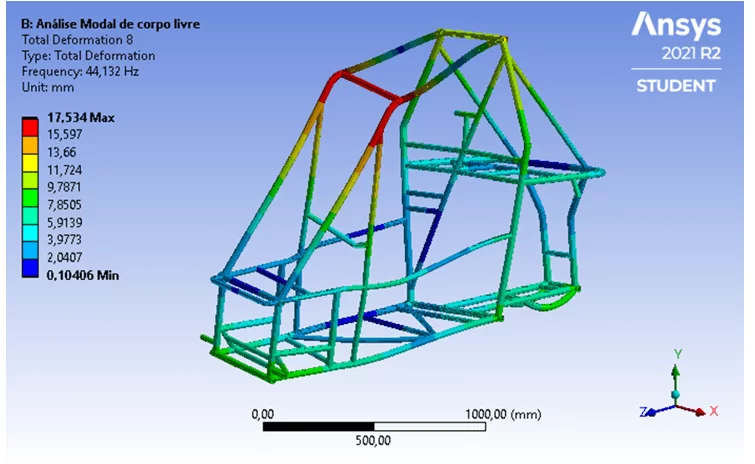
Isto posto, identifica-se a zona superior e frontal do veículo nas proximidades do teto como uma zona crítica, uma vez que apresenta as maiores deformações quando a gaiola é submetida a frequências de excitação.
5.2 ANÁLISE MODAL DE CORPO RÍGIDO
Na análise de corpo rígido, os pontos de ancoragem das bandejas ao chassi são tomados como fixos. Nessa análise, considera-se as excitações transmitidas quando o veículo transpõe obstáculos que possuem padrões de repetição com uma periodicidade definida, a exemplo de assimetrias do tipo “costela de vaca”, que contém saliências e depressões. Em geral, toma-se os seis primeiros modos de vibrar, cujas frequências são apresentadas na Tabela 4.
Tabela 4 – Seis primeiros modos de vibrar da estrutura.
| Modo | Frequência (Hz) | Comportamento |
| 1 | 47,738 | Flexão |
| 2 | 52,681 | Flexão |
| 3 | 60,148 | Torção |
| 4 | 80,283 | Torção |
| 5 | 83,523 | Torção e Flexão |
| 6 | 114,38 | Torção e Flexão |
Fonte: Autoria própria (2021).
Analisando os resultados obtidos, encontra-se uma faixa de frequência de 47,738 a 114,38 Hz. Dessa forma, em condições de pistas com obstáculos, o modelo também resiste às oscilações causadas pelo motor e as irregularidades nas pistas.
Com base na análise, observa-se que os dois primeiros modos de vibrar do chassi provocam deformações de flexão nos tubos e concentração de tensão nas uniões soldadas, enquanto o quarto e o quinto modos de vibrar estão relacionados a cenários de torção.
Na Figura 10, observa-se o terceiro modo de vibrar mostrando um cenário de torção, que provoca deformações na parte superior e frontal da gaiola.
Figura 10 – Comportamento de torção no terceiro modo de vibrar.
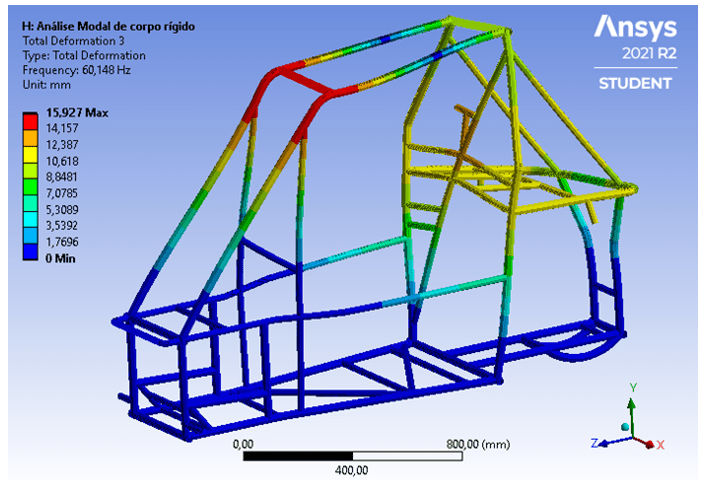
Por fim, os dois últimos modos analisados (5º e 6º) geram deformações e deflexões na estrutura obtidas de esforços combinados de torção e flexão, os quais são gerados quando o veículo trafega em pistas com irregularidades em oposição de fase entre as rodas do lado direito e esquerdo. A Figura 11 apresenta o comportamento da estrutura no sexto modo de vibrar.
Figura 11 – Comportamento combinado de torção e flexão no sexto modo de vibrar.
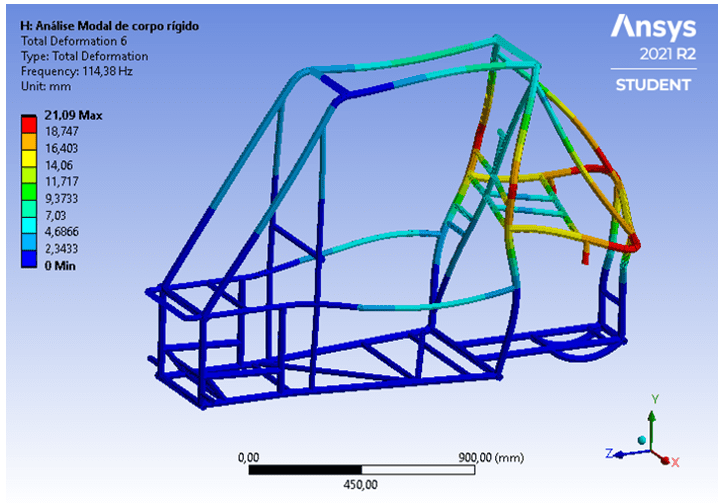
Nesse contexto, para evitar grandes deformações dos tubos que interligam os lados do veículo, o piloto deve conduzir o veículo em uma velocidade que não provoque frequências de excitação próximas da frequência de tais modos. Por isso, é importante que as seis primeiras frequências da estrutura da gaiola estejam em um intervalo distante das frequências de excitação dos obstáculos com comportamentos senoidais.
5.3 CENÁRIO DE TORÇÃO
O cenário de torção leva em consideração as cargas assimétricas às quais o chassi é submetido quando uma ou mais rodas são erguidas (saliência) ou abaixadas (reentrância) durante a transposição de obstáculos. Além do mais, a magnitude da força exercida sobre as rodas e os elementos de suspensão depende das massas dos componentes, conforme apresentado na Tabela 2 anteriormente.
Nessa situação, aplicou-se um binário de forças de 4410 N nos cubos de roda dianteiros, mantendo os cubos de roda traseiros fixos. Na Figura 12, é possível visualizar o local no chassi onde as tensões combinadas devido à torção são mais elevadas.
Figura 12 – Gradiente de tensões axiais e de curvatura devido a torção.
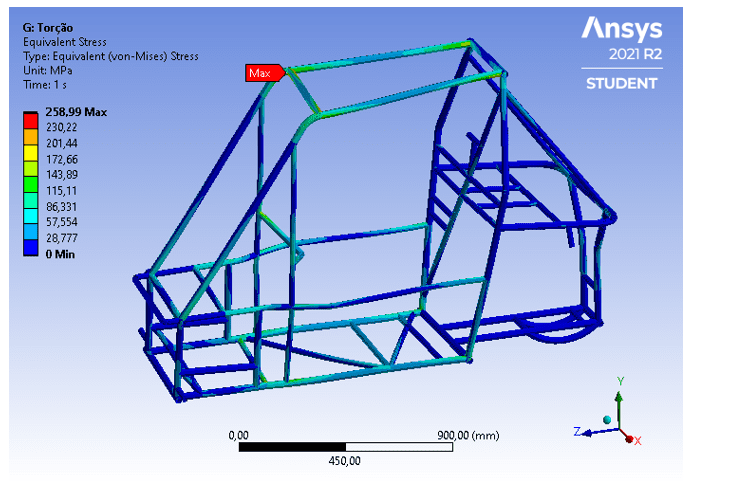
O valor máximo para as tensões está localizado na junção entre os tubos superiores que formam o teto do veículo, com intensidade aproximada de 258,99 MPa. Tendo a tensão de escoamento (351 MPa) como tensão de falha, nota-se que os resultados são aceitáveis, visto que a estrutura atua no regime elástico com um fator de segurança de aproximadamente 1,35.
Além disso, a Figura 13 mostra que o deslocamento máximo obtido é de 13,6 mm e menor que a deflexão máxima de 152 mm exigida pelo regulamento da competição Baja SAE.
Figura 13 – Deformação da estrutura no cenário de torção.
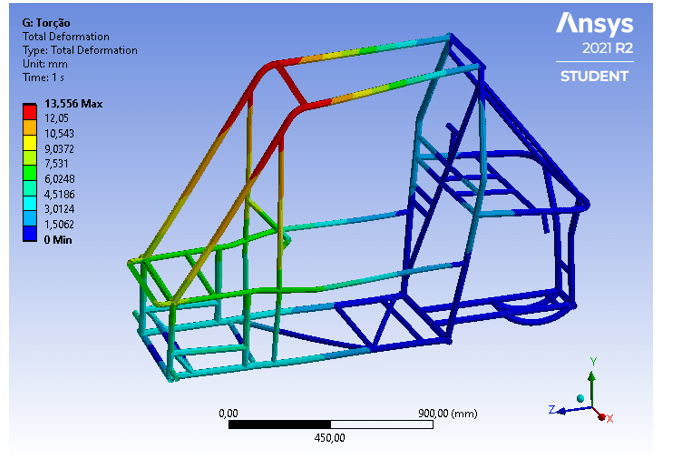
5.4 CAPOTAMENTO
No cenário de capotamento, é aplicada uma força de 9800 N sobre os tubos que compõem o teto do veículo, considerando que os tubos formadores do piso são fixos. Na Figura 14, observa-se que a tensão máxima de 268,8 MPa se localiza na união soldada entre os tubos do teto e os tubos verticais que formam a parede corta-fogo.
Figura 14 – Gradiente de tensões axiais e de curvatura no capotamento.
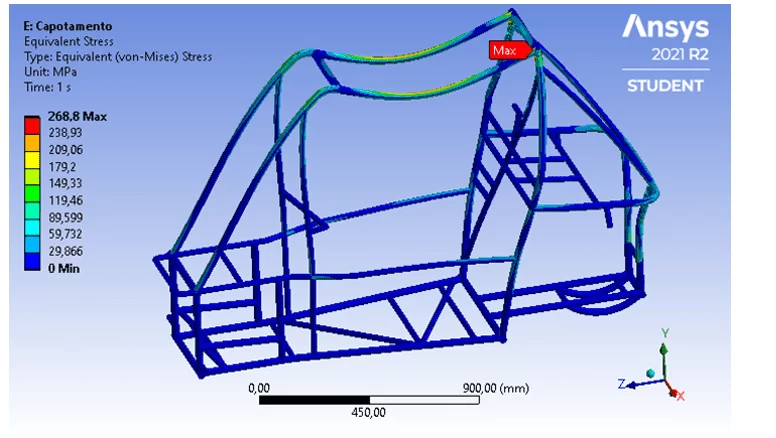
Por conseguinte, uma vez que a tensão de escoamento do aço SAE 1020 é de 351 MPa, verifica-se que a estrutura do chassi apresenta um bom comportamento diante de um cenário crítico nas competições, haja vista que possui um coeficiente de segurança de 1,3 e não se deforma plasticamente.
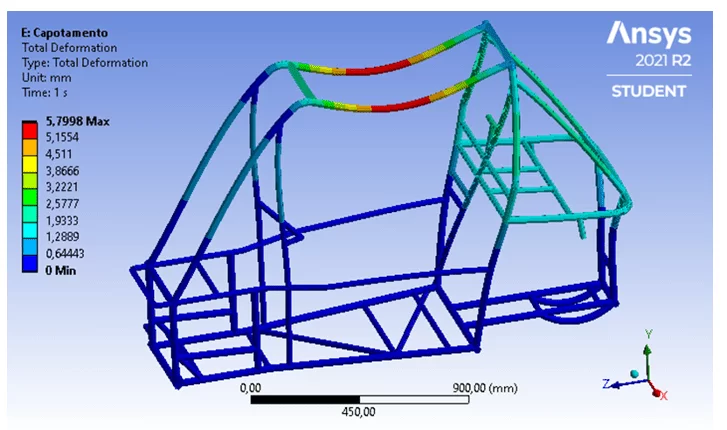
Ademais, com base na Figura 15, é possível observar que o deslocamento máximo de aproximadamente 5,8 mm encontrado na região superior da estrutura é muito menor que a deflexão máxima de 152 mm exigida pela norma.
Figura 15 – Deformação da estrutura no capotamento.
5.5 IMPACTO LATERAL
Esse cenário simula uma colisão entre dois veículos, de modo que um sofre choque lateral e o outro recebe um impacto frontal. No choque lateral, o veículo é submetido a uma força de 3675 N em um dos lados, tomando como fixos os tubos do lado oposto.
A Figura 16 apresenta as tensões encontradas, sendo possível observar uma tensão máxima de 205,95 MPa na solda entre o tubo horizontal que liga a parte frontal e traseira do veículo e os tubos verticais que formam a parede corta-fogo.
Figura 16 – Gradiente de tensões no impacto lateral.
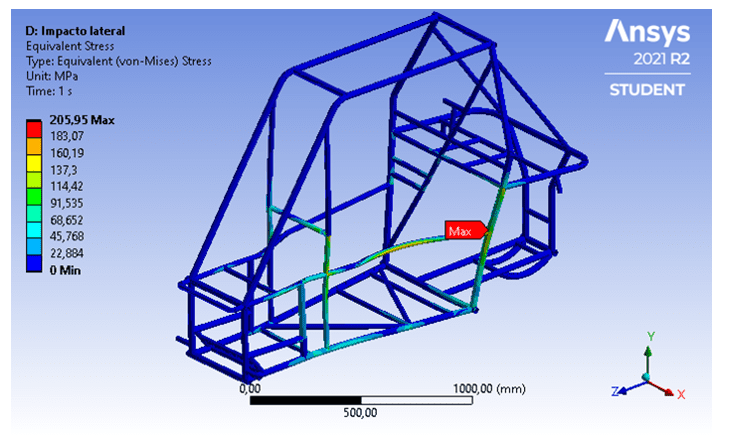
Nesse sentido, tendo em vista que a tensão de escoamento do aço SAE 1020 é de 351 MPa, nota-se que a estrutura não sofre deformação plástica, atuando com um coeficiente de segurança de 1,7.
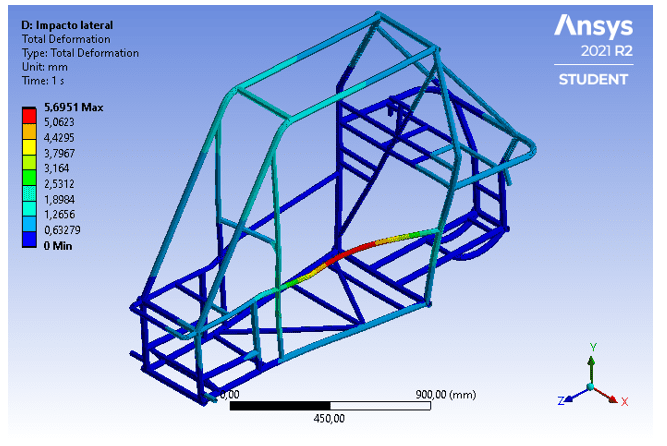
Além disso, visto que a deformação máxima na lateral é de aproximadamente 5,9 mm e o limite exigido pela norma é de 152 mm, o objetivo de manter a segurança do piloto é cumprido. Dessa maneira, a Figura 17 ilustra o comportamento da estrutura, sendo válido ressaltar que o resultado obtido é coerente devido ao grande comprimento dos tubos horizontais em questão, o que aumenta o risco de flambagem.
Figura 17 – Deformação da estrutura devido ao impacto lateral.
5.6 IMPACTO FRONTAL
Num cenário de colisão frontal, as forças de impacto são aplicadas no sentido contrário ao movimento do veículo para simular uma força contrária de modo a desacelerá-lo em pouco tempo. Nesse sentido, como condição de contorno, uma força de 2450 N é aplicada diretamente no para-choque do veículo e distribuída ao longo do seu comprimento, visto que é o componente responsável por sofrer as primeiras deformações oriundas de impactos frontais. A Figura 18 apresenta os resultados da análise.
Figura 18 – Gradiente de tensões no impacto frontal.
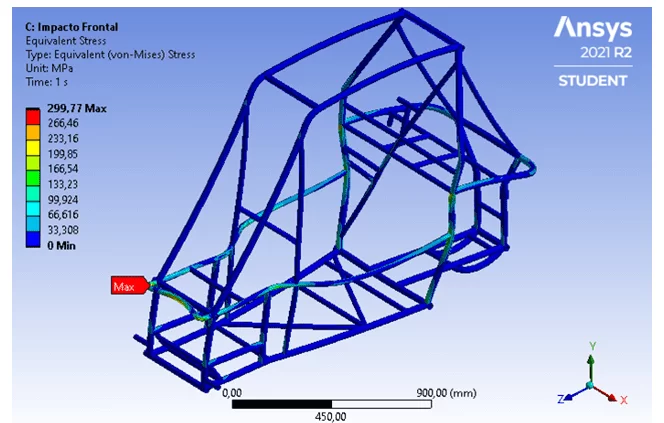
Com base na Figura 18, tem-se que o valor máximo de tensão está localizado nas junções do para-choque com o seu elemento fixador, com intensidade de 299,77 MPa. À vista disso, constata-se que a estrutura atua no regime elástico com um fator de segurança de 1,2.
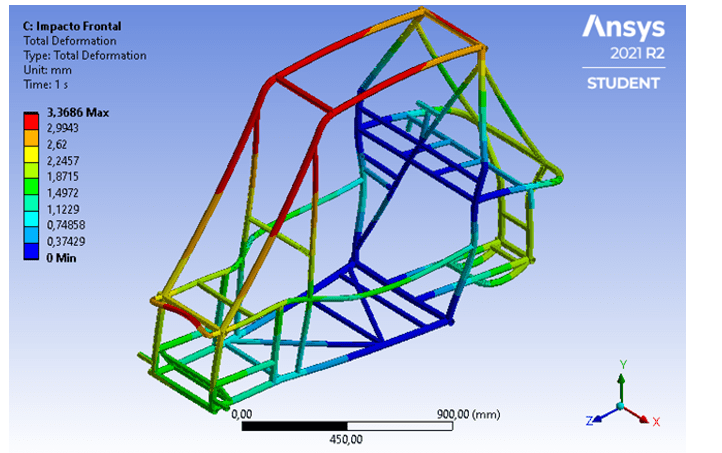
Ademais, na Figura 19, é possível observar que o deslocamento máximo obtido é de aproximadamente 3,4 mm, ou seja, uma deformação bastante inferior à deflexão máxima de 152 mm exigida pelo regulamento Baja SAE. Dessa forma, o para-choque cumpre com a sua finalidade de absorver impactos.
Figura 19 – Deformação da estrutura devido ao impacto frontal.
Os resultados encontrados apontam que, embora em condições extremas de carregamentos e vibrações, os componentes do chassi não apresentam risco de falha por fratura durante as competições, haja vista que, em geral, as cargas aplicadas ao veículo são inferiores às consideradas nas análises. Além disso, os deslocamentos provocados em todos os cenários são menores que as deformações máximas exigidas pelos organizadores das competições Baja SAE.
6. CONSIDERAÇÕES FINAIS
Neste trabalho, foi proposta uma metodologia de análise modal e de análise estática linear da estrutura do chassi de um veículo do tipo Baja a partir do Método dos Elementos Finitos. Para isso, foram utilizados métodos semelhantes aos utilizados em nível industrial.
Os processos de análise foram realizados no módulo estrutural do software ANSYS Workbench, desenvolvendo uma malha apropriada e definindo adequadamente as condições de contorno necessárias. Nas análises, os componentes de base do chassi foram engastados, o que representa uma situação crítica de operação do veículo, considerando-se que os componentes de suspensão são capazes de dissipar as forças aplicadas. Além do mais, foram aplicadas cargas sobre barras específicas, o que também se enquadra em uma situação crítica, visto que, na maioria dos casos de capotamento e colisão, o impacto é distribuído sobre outras barras.
Por meio das análises estruturais, é possível observar que as tensões as quais atuam na gaiola são inferiores à tensão de escoamento do aço SAE 1020, material utilizado na fabricação dos tubos do chassi.
Portanto, considerando que as análises foram realizadas em condições críticas, o chassi apresenta bom comportamento mecânico e resultados satisfatórios de rigidez quando submetido aos diversos tipos de carregamento presentes nas competições. Outrossim, é importante observar que, respeitando os limites de segurança exigidos, as deformações controladas da estrutura do chassi são necessárias para absorver e dissipar a energia oriunda de carregamentos externos, diminuindo o impacto transmitido ao piloto e protegendo-o de lesões, o que proporciona confiabilidade e segurança à gaiola.
Todavia, no cenário de torção, a parte superior do chassi sofre uma deformação que destoa dos outros casos. Isso sugere que a geometria desse local seja modificada pela adição de alguns tubos horizontais ou transversais para aumentar a distribuição de massa local e servir como reforço estrutural.
Outrossim, por meio das análises de vibrações realizadas, nota-se que a estrutura do chassi resiste às oscilações causadas pelo motor e pelos obstáculos presentes nas pistas de competição, os quais provocam forças de natureza harmônicas aplicadas ao veículo.
Logo, com base nos resultados, verifica-se que a estrutura do chassi é eficaz, segura e robusta o suficiente para resistir aos esforços aplicados, cumprindo então com o seu objetivo.
Para trabalhos futuros, sugere-se um estudo dinâmico apoiado na adição dos componentes de suspensão, como o amortecedor, a fim de analisar a estrutura em condições ainda mais próximas da realidade.
REFERÊNCIAS
AUSTRALIAN, G. Australian desing rule Adr59. Omnibuses Rollover Protective Structures, 2012. Disponível em: < https://www.legislation.gov.au/Series/F2007L04077>. Acesso em: 25 set. 2021.
DANTAS, Kainã Vieira. Dimensionamento de freios para veículos baja sae: estudo de caso cactus baja. 2019. 77 f. Monografia (Bacharelado em Engenharia Mecânica) – Universidade Federal Rural do Semi-Árido, Mossoró, 2019.
FURTADO, Daniel Canongia. Análise estrutural de chassi de veículos automotivos. 2013. 77 f. Monografia (Bacharelado em Engenharia Automotiva) – Universidade de Brasília, Brasília, 2013.
GILLESPIE, Thomas. Fundamentals of Vehicle Dynamics. 1.ed. Warrendale: SAE International, 1992. 520 p.
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de Física: Gravitação, Ondas e Termodinâmica. 8.ed. Rio de Janeiro: LTC, 2009. 310p.
HAPPIAN-SIMITH, Julian. An introduction to modern vehicle design. 1.ed. Oxford: Elsevier, 2001. 632p.
KABILAN, Kaushik Munusam; MURKUTE Akshay; MARATHE, Anket Hirachand; RODRIGUES, Ivan; RAMAGIRI, Karthik. Structural otimization of sae baja car frame. 2016. Disponível em: <https://designinformaticslab.github.io/_teaching//designopt/projects/2016/desopt_2016_01.pdf>. Acesso em: 15 set. 2021.
LOTTERMANN, João Pedro Taborda. Projeto estrutural de chassi tipo gaiola para veículos minibaja: análise numérica e experimental. 2014. 97 f. Monografia (Bacharelado em Engenharia Automotiva) – Universidade de Brasília, Brasília, 2014.
MEIROVITCH, Leonard. Elements of Vibration Analysis. Califórnia: McGraw-Hill International Editions, Mechanical Engineering Series, 1986. 576p.
PAWLOWSKI, Janusz. Vehicle Body Engineering. Londres: Business Books, 1969. 300p.
SAE BRASIL. Regulamento Administrativo e Técnico Baja Sae Brasil. 2021. Disponível em: <https://saebrasil.org.br/programas-estudantis/baja-sae-brasil/regras-e-relatorios-2/>. Acesso em: 10 set. 2021.
[1] Graduando em Engenharia Mecânica. ORCID: https://orcid.org/0000-0003-4858-6314.
[2] Graduando em Engenharia Mecânica e Técnico em Eletromecânica pelo Instituto Federal de Sergipe. ORCID: https://orcid.org/0000-0001-6791-5422.
Enviado: Novembro, 2021.
Aprovado: Dezembro, 2021.
