ARTIGO ORIGINAL
DANTAS, Isabela Franco [1], RIES, Lisandra Kittel [2], PADILHA, Juliano Bitencourt [3]
DANTAS, Isabela Franco. RIES, Lisandra Kittel. PADILHA, Juliano Bitencourt. Projeto de um filtro passivo para correção das distorções harmônicas de corrente em uma subestação. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 10, Vol. 03, pp. 05-17. Outubro de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/filtro-passivo
RESUMO
As distorções harmônicas provocam efeitos negativos na qualidade da energia, entre eles, o mau funcionamento, o aumento de temperatura e a diminuição da vida útil dos equipamentos. Existem algumas normas regulamentadoras que limitam a quantidade de distorções harmônicas causadas pela conexão das cargas não lineares à rede elétrica. Neste contexto, a seguinte questão norteadora surge: como podemos atender determinadas normas de qualidade de energia por meio da utilização de filtros passivos? Visando a responder a essa pergunta, este artigo tem como objetivo apresentar uma metodologia de projeto de filtros passivos de harmônicas e verificar a eficiência desta filtragem utilizando os limites de distorção previstos em norma. O local deste estudo é no quarto transformador da subestação do IFSC, Câmpus Florianópolis, onde foram realizadas medições práticas que serão trazidas para análise dos efeitos das distorções harmônicas na qualidade da energia da subestação. Um projeto de filtro passivo série ressonante é apresentado para correção dessas distorções. Por meio de simulações será mostrada uma análise da eficiência de filtragem com o intuito de verificar os efeitos da implantação do filtro na instalação. Mostra-se que o principal objetivo é cumprido uma vez que os limites recomendados pela norma são respeitados.
Palavras-chave: Distorções harmônicas, Qualidade da energia, Filtros passivos de harmônicas.
1. INTRODUÇÃO
A maioria dos equipamentos eletrônicos possuem semicondutores como diodos e transistores, caracterizando uma carga não linear. Quando cargas não lineares são conectadas à rede elétrica, surgem correntes harmônicas que causam prejuízos para diversos equipamentos. As perturbações harmônicas podem gerar sobrecarga nos condutores de neutro, deformação da tensão de alimentação, perturbação das redes de comunicação, além de causar sobrecarga, vibrações e envelhecimento em motores, transformadores e alternadores (PROCOBRE; SCHNEIDER ELECTRIC, 2003).
Existem comitês de normatização que estudam os efeitos causados pelas cargas não lineares no sistema elétrico. No Brasil, a ANEEL (Agência Nacional de Energia Elétrica), órgão regulador do assunto, normatiza as distorções harmônicas de tensão (PRODIST Módulo 8). Outro comitê de normatização é o IEEE (Institute of Electrical and Electronics Engineers). Este estudo leva em consideração a norma IEEE 519-2014 que recomenda os limites para distorções harmônicas de corrente, levando em consideração tensões entre 120 V e 69 kV.
Após a comprovação de que os limites de distorção harmônica foram ultrapassados, é possível efetuar uma correção para manter as distorções dentro do limite com a implantação de filtros, podendo ser eles ativos ou passivos. Os filtros passivos se caracterizam pelo uso de elementos passivos: resistores, capacitores e indutores. Já os filtros ativos utilizam semicondutores para corrigir as correntes harmônicas (QUADROS, 1999).
Neste contexto, a seguinte questão norteadora surge: como podemos atender determinadas normas de qualidade de energia por meio da utilização de filtros passivos? Visando a responder a essa pergunta, este artigo tem como objetivo apresentar uma metodologia de projeto de filtros passivos de harmônicas e verificar a eficiência desta filtragem utilizando os limites de distorção previstos na norma IEEE 519-2014.
Este trabalho utiliza o método de filtros passivos para realizar um estudo de caso para correção da distorção harmônica de corrente de 3ª e 5ª ordem, no quarto transformador da subestação do IFSC, Câmpus Florianópolis. Os dados utilizados para efetuar tal correção foram extraídas do artigo “Avaliação de Distorções Harmônicas e Desequilíbrios de Tensão e de Corrente na Subestação do IFSC Câmpus Florianópolis” (DUPCZAK et al., 2018) e do trabalho de conclusão de curso “Estudo Sobre a Utilização de Filtros Passivos para Redução de Conteúdo Harmônico nas Instalações Elétricas do IFSC – Câmpus Florianópolis” (TEODORO, 2019). A escolha pela utilização de filtros passivos baseou-se, principalmente, pela sua alta confiabilidade, além de seu baixo custo de implementação (QUADROS, 1999).
Este artigo está organizado em seis seções. A primeira seção descreve o local escolhido para correção das distorções harmônicas. A segunda seção apresenta como foi realizada a modelagem do filtro para a correção da planta elétrica do local escolhido. A terceira seção traz a análise e os resultados de simulação obtidos para a planta elétrica real sem o filtro. A quarta seção, semelhante à anterior, descreve a análise e os resultados de simulação obtidos para a planta elétrica agora com o filtro projetado. A quinta seção apresenta os resultados com a análise comparativa dos dados obtidos da planta real com e sem o filtro. Na última seção é apresentada a conclusão deste artigo.
2. LOCAL ESCOLHIDO
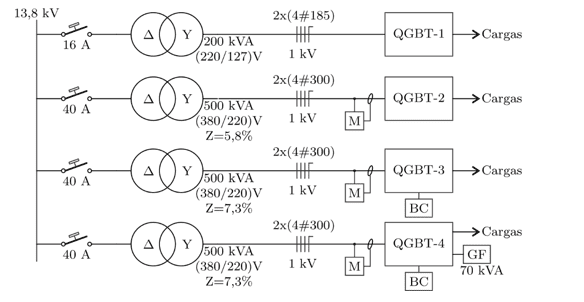
O diagrama unifilar simplificado da subestação do IFSC Câmpus Florianópolis é apresentado na Figura 1. No diagrama é possível verificar quatro quadros gerais de baixa tensão (QGBT), porém para análise será desconsiderado o QGBT-1, pois ele se encontra desativado. O QGBT-2, o QGBT-3 e o QGBT-4 estão conectados a três transformadores trifásicos a seco. Os módulos fotovoltaicos de geração de energia e os bancos de capacitores automatizados para correção do fator de potência estão representados pelas caixas com as inscrições GF e BC, respectivamente, sendo o primeiro presente apenas no QGBT-4 e o segundo no QGBT-3 e QGBT-4. As caixas com a letra M representam os locais onde foram realizadas as medições de tensão e corrente utilizadas no trabalho.
Figura 1 – Diagrama unifilar simplificado da subestação do IFSC Câmpus Florianópolis
As medições na subestação do IFSC foram analisadas em 2018 com o uso do analisador de qualidade de energia CW500 do fabricante Yokogawa e comparadas com os limites de distorção da norma IEEE 519-2014 apresentada na Tabela 1. A Tabela 2 (DUPCZAK et al., 2018) mostra os valores percentuais das harmônicas e da distorção total da demanda (TDD) e servem de ponto de partida para o projeto do filtro passivo.
Tabela 1 – Limites de distorção de corrente para tensões entre 120 V e 69 kV
| Distorção Harmônica Máxima da Corrente em Percentagem de IL | ||||||
| h: Ordem das Harmônicas Ímpares | ||||||
| ISC/IL | h < 11 | 11 ≤ h < 17 | 17 ≤ h < 23 | 23 ≤ h < 35 | 35 ≤ h | THD |
| < 20* | 4,0% | 2,0% | 1,5% | 0,6% | 0,3% | 5,0% |
| 20 < 50 | 7,0% | 3,5% | 2,5% | 1,0% | 0,5% | 8,0% |
| 50 < 100 | 10,0% | 4,5% | 4,0% | 1,5% | 0,7% | 12,0% |
| 100 < 1000 | 12,0% | 5,5% | 5,0% | 2,0% | 1,0% | 15,0% |
| > 1000 | 15,0% | 7,0% | 6,0% | 2,5% | 1,4% | 20,0% |
| As harmônicas pares são limitadas a 25% do limite da harmônica ímpar imediatamente superior | ||||||
| Não é permitido componente contínua (Retificadores de meia-onda, por exemplo) | ||||||
| * Todos os equipamentos de geração de energia elétrica são limitados pelos valores desta linha, independe de sua capacidade de curto-circuito ISC/IL | ||||||
| ISC: Corrente de curto-circuito máxima no PCC.
IL: Corrente máxima solicitada pela carga, na frequência fundamental, no PCC. É recomendado que IL seja calculada como a média da máxima corrente demandada nos 12 meses precedentes. |
||||||
Fonte: IEEE Std 519-2014, adaptado por Kassick (2016).
Tabela 2 – Limites de distorção de corrente para tensões entre 120 V e 69 kV
| QGBT | 3 < h < 11 | 11 ≤ h < 17 | 17 ≤ h < 23 | 23 ≤ h < 35 | 35 ≤ h < 50 | TDD |
| 2 | 4,3% | 0,3% | 0,2% | 0,0% | 0,0% | 4,8% |
| 6,2% | 0,5% | 0,1% | 0,1% | 0,0% | 6,4% | |
| 4,3% | 0,2% | 0,1% | 0,1% | 0,0% | 4,5% | |
| 3 | 7,1% | 0,4% | 0,2% | 0,0% | 0,0% | 8,0% |
| 7,0% | 0,3% | 0,1% | 0,0% | 0,0% | 8,1% | |
| 5,8% | 0,2% | 0,0% | 0,0% | 0,0% | 7,2% | |
| 4 | 9,3% | 0,7% | 0,4% | 0,0% | 0,0% | 9,8% |
| 7,4% | 0,5% | 0,1% | 0,0% | 0,0% | 7,8% | |
| 10,4% | 0,6% | 0,2% | 0,0% | 0,0% | 10,7% |
Fonte: Dupczak et al. (2018).
Ao observar os dados da Tabela 2, é possível verificar que o problema se encontra entre as terceiras e décimas primeiras harmônicas em todos os QGBTs, mostrando valores acima dos recomendados pela norma IEEE 519-2014. Além disso, dentre os QGBTs, o que apresenta maior TDD é o QGBT-4, por esse motivo o filtro shunt para correção das harmônicas de corrente será inserido apenas nele.
3. PROJETO DO FILTRO
O filtro passivo escolhido é do tipo RLC série conforme apresentado na Figura 2. Considerando que o projeto do filtro passivo será realizado para 3ª e 5ª ordem, no quarto transformador localizado no QGBT-4 da subestação do IFSC Câmpus Florianópolis, dois filtros RLC serão calculados e distribuídos entre as 3 fases desse QGBT.
Figura 2 – Filtro passivo que será projetado para conexão entre as fases e o neutro do QGBT-4
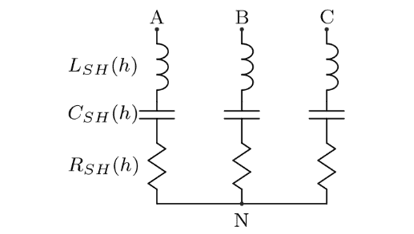
Este filtro também é conhecido como filtro shunt sintonizado (QUADROS, 1999) e será implantado entre a fase e o neutro do sistema. Segundo Quadros (1999, p. 8) “A sintonia é feita ajustando os valores do indutor (LSH) e do capacitor (CSH) de tal forma que na frequência de ressonância (f0) a impedância seja apenas a resistência dos enrolamentos do indutor associada à resistência interna do capacitor (RSH)”.
A distribuição das unidades capacitivas considera que 60% da capacitância total disponível estará presente para filtragem da harmônica de ordem 3 (f0 = 3∙60 = 180 Hz) e os 40% restantes para harmônica de ordem 5 (f0 = 5∙60 = 300 Hz). Os valores das unidades capacitivas de 45,90 μF (2,50 kVAr/380 V) e 91,84 μF (5,0 kVAr/380 V) foram utilizados por serem respectivos aos capacitores dos bancos ligados ao QGBT-3 e QGBT-4, já citados. Após o cálculo das capacitâncias associadas ao filtro (CSH), calcula-se a indutância do filtro shunt com a equação LSH = 1/(2∙π∙f02∙CSH), considerando os respectivos valores de frequência de ressonância (f0). Por fim, calcula-se a resistência do filtro shunt conforme a equação RSH = (2∙π∙f0∙LSH)/QSH, onde QSH é o fator de qualidade do indutor do filtro. O fator de qualidade é inversamente proporcional a perda de energia no filtro e diretamente a perda de sintonia, ou seja, quanto maior o QSH menor a perda de energia e maior a possibilidade de perda de sintonia (KASSICK, 2016). Para a modelagem do filtro foi atribuído um valor igual a 100 para o QSH. Os parâmetros calculados do filtro passivo estão resumidos na Tabela 3.
Tabela 3 – Parâmetros do filtro shunt utilizados na simulação
| Ordem do filtro | Unidades Capacitivas
(91,84 Μf) |
Unidades
Capacitivas (45,94 Μf) |
Capacitância
(Μf) |
Indutância
(Μh) |
Resistência
( ) |
| h = 3 | 13 | 1 | 1239,82 | 630,57 | 7,13 |
| h = 5 | 9 | 0 | 826,56 | 340,50 | 6,41 |
Fonte: elaboração própria.
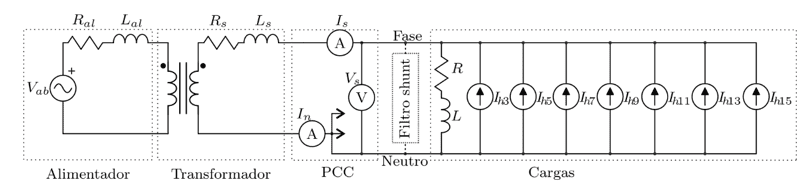
A Figura 3 mostra o circuito de uma das fases do QGBT-4, o qual apresenta o local de inserção do filtro shunt. A impedância do alimentador é representada por Ral e Lal. Esses valores correspondem à impedância acumulada no ponto de conexão e são informações fornecidas pela concessionária. Os valores Rs e Ls representam as características dos transformadores no lado em Y. Esses valores são obtidos após a análise da Figura 1, onde os dados nominais de base para cada transformador conectado aos QGBTs são apresentados. As variáveis que serão utilizadas para análise são medidas no Ponto de Conexão Comum (PCC), representadas por Vs (tensão de fase), Is (corrente de fase) e In (corrente de neutro). Além disso, a Figura 3 expõe as correntes harmônicas inseridas, representando as cargas não lineares. Para as outras fases e outros QGBTs, o mesmo circuito é replicado.
Figura 3 – Esquemático de uma do QGBT-4 da simulação feita no software PSIM. Variáveis medidas: Vs, Is e In. O filtro é conectado entre a fase e o neutro do lado em Y do transformador
4. ANÁLISE E DADOS OBTIDOS DA PLANTA REAL SEM O FILTRO
Na Tabela 4 são exibidos os resultados de simulação de cada fase dos QGBTs da planta sem o filtro. Mostra-se a THD (Taxa de Distorção Harmônica) de tensão e corrente, o fator de potência (FP), a potência ativa (P), a potência aparente (S), a tensão eficaz (Vs,ef) e a corrente eficaz (Is,ef).
Tabela 4 – Valores das grandezas obtidas nas simulações considerando a planta sem o filtro
| QGBT-2 sem filtros | |||||||
| Fase | FP | P (Kw) | S (Kva) | THD(v) (%) | THD(i) (%) | Vs,ef (V) | Is,ef (A) |
| A | 0,9493 | 51,8344 | 54,6007 | 0,4730 | 5,66258 | 229,0760 | 238,3520 |
| B | 0,9737 | 54,9311 | 56,4142 | 0,5376 | 7,31027 | 226,7911 | 229,1910 |
| C | 0,9428 | 48,8903 | 51,8536 | 0,4240 | 5,60240 | 229,0053 | 226,4296 |
| QGBT-3 sem filtros | |||||||
| Fase | FP | P (Kw) | S (Kva) | THD(v) (%) | THD(i) (%) | Vs,ef (V) | Is,ef (A) |
| A | 0,9397 | 36,4943 | 38,8370 | 1,7211 | 11,2102 | 229,4644 | 169,2509 |
| B | 0,9576 | 30,0880 | 31,4208 | 0,7163 | 10,5044 | 229,7681 | 136,7502 |
| C | 0,9361 | 37,4008 | 39,9537 | 1,9894 | 11,3101 | 229,5638 | 174,2614 |
| QGBT-4 sem filtros | |||||||
| Fase | FP | P (Kw) | S (Kva) | THD(v) (%) | THD(i) (%) | Vs,ef (V) | Is,ef (A) |
| A | 0,8365 | 77,4419 | 92,5791 | 1,38412 | 9,6566 | 225,1658 | 411,1599 |
| B | 0,8382 | 104,7025 | 124,9105 | 1,3989 | 7,0054 | 222,7268 | 560,8237 |
| C | 0,8354 | 73,2378 | 87,66201 | 1,3691 | 10,6928 | 225,3891 | 388,9366 |
Fonte: elaboração própria.
O valor de pico da componente fundamental (h = 1) e das componentes harmônicas da corrente Is (3 ≤ h ≤ 15) são apresentados na Tabela 5 para cada fase dos QGBTs para planta sem o filtro.
Tabela 5 – Valores de pico das componentes harmônicas para cada fase dos QGBTs sem o filtro
| Componente harmônica de corrente (A) | QGBT | ||||||||
| 2 | 3 | 4 | |||||||
| A | B | C | A | B | C | A | B | C | |
| h = 1 | 336,56 | 347,16 | 319,71 | 237,88 | 192,33 | 244,88 | 578,81 | 791,15 | 546,92 |
| h = 3 | 16,69 | 24,32 | 16,84 | 17,94 | 16,16 | 16,01 | 51,9 | 51,9 | 55,8 |
| h = 5 | 8,17 | 6,48 | 5,08 | 10,76 | 11,08 | 12,44 | 16,56 | 17,46 | 14,76 |
| h = 7 | 1,14 | 2,63 | 2,33 | 3,31 | 2,84 | 4,04 | 7,21 | 8,37 | 6,7 |
| h = 9 | 1,93 | 2,69 | 2,34 | 1,64 | 1,16 | 3,08 | 6,09 | 5,59 | 5,51 |
| h = 11 | 1,16 | 1,94 | 0,92 | 2,38 | 1,95 | 1,74 | 3,74 | 3,15 | 3,15 |
| h = 13 | 0,74 | 0,71 | 0,78 | 3,38 | 2,62 | 2,69 | 2,43 | 2,13 | 2,2 |
| h = 15 | 0,65 | 1,05 | 0,35 | 15,28 | 2,67 | 18,17 | 1,83 | 1,31 | 1,49 |
Fonte: elaboração própria.
A Tabela 6 mostra o valor da amplitude das componentes harmônicas da corrente de neutro e o valor eficaz da corrente de neutro dos QGBTs.
Tabela 6 – Valores de pico das amplitudes das componentes harmônicas da corrente de neutro e o valor eficaz da corrente de neutro dos QGBTs considerando a planta sem o filtro
| Componente harmônica de corrente (A) | QGBT | ||
| 2 | 3 | 4 | |
| h = 1 | 52,23 | 51,96 | 229,88 |
| h = 3 | 57,75 | 50,08 | 159,59 |
| h = 9 | 6,95 | 3,1 | 17,19 |
| h = 15 | 2,04 | 1,08 | 4,62 |
| Valor eficaz da corrente (A) | 55,3734 | 51,0956 | 198,2928 |
Fonte: elaboração própria.
Esses valores, auferidos da simulação, serão comparados com os valores da planta após a inserção do filtro projetado.
5. ANÁLISE E DADOS OBTIDOS DA PLANTA APÓS A INSERÇÃO DO FILTRO CALCULADO
O filtro calculado na Tabela 3 é inserido no circuito da Figura 3. A Tabela 7 mostra os resultados de simulação para cada fase dos QGBTs da planta com o filtro. Obtiveram-se as THDs de tensão e corrente, além das grandezas: FP, P, S, Vs,ef e Is,ef. É possível verificar o aumento do FP e redução das THDs para o QGBT-4.
Tabela 7 – Valores das grandezas obtidas nos QGBTs considerando a planta com o filtro
| QGBT-2 com filtros | |||||||
| Fase | FP | P (kW) | S (kVA) | THD(v) (%) | THD(i) (%) | Vs,ef (V) | Is,ef (A) |
| A | 0,9493 | 51,9662 | 54,7395 | 0,4464 | 5,6643 | 229,3666 | 238,6549 |
| B | 0,9737 | 55,0681 | 56,5548 | 0,5172 | 7,3079 | 229,4763 | 246,4514 |
| C | 0,9428 | 49,0138 | 51,9846 | 0,3976 | 5,6027 | 229,2943 | 226,7156 |
| QGBT-3 com filtros | |||||||
| Fase | FP | P (kW) | S (kVA) | THD(v) (%) | THD(i) (%) | Vs,ef (V) | Is,ef (A) |
| A | 0,9397 | 36,5871 | 38,9348 | 1,7107 | 11,189 | 229,7553 | 169,4619 |
| B | 0,9576 | 30,1631 | 31,4977 | 0,6908 | 10,4617 | 230,054 | 136,9146 |
| C | 0,9361 | 37,4953 | 40,0565 | 1,9998 | 11,348 | 229,5644 | 174,489 |
| QGBT-4 com filtros | |||||||
| Fase | FP | P (kW) | S (kVA) | THD(v) (%) | THD(i) (%) | Vs,ef (V) | Is,ef (A) |
| A | 0,9959 | 80,492 | 80,8212 | 0,522 | 2,0602 | 229,3307 | 352,4223 |
| B | 0,9719 | 108,7136 | 111,8559 | 0,5263 | 1,4524 | 226,7911 | 493,2111 |
| C | 0,9982 | 76,1419 | 76,2747 | 0,4965 | 2,0737 | 229,5638 | 332,2592 |
Fonte: elaboração própria.
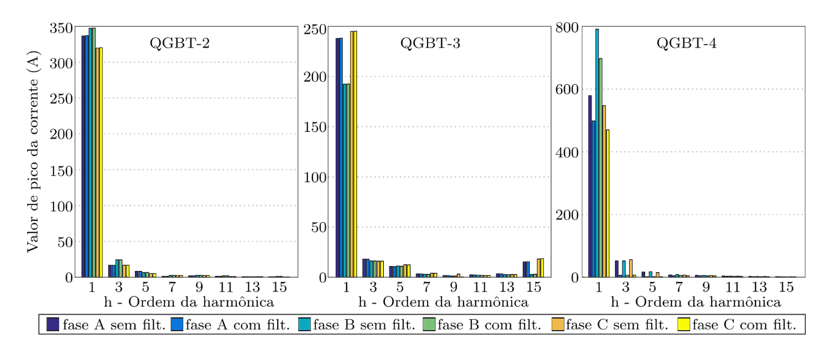
O valor de pico das componentes harmônicas de corrente para cada fase dos QGBTs da planta com filtro é apresentado na Tabela 8. Ao comparar com a planta sem filtro, Tabela 5, é possível verificar que todas as componentes harmônicas do QGBT-4 (3 ≤ h ≤ 15) sofreram redução após a inserção do filtro, enquanto os QGBT-2 e QGBT-3 não apresentaram modificação no valor de pico das componentes harmônicas com a inserção do filtro no QGBT-4.
Tabela 8 – Valor de pico das componentes harmônicas de cada fase dos QGBTs considerando a planta com o filtro
| Componente harmônica de corrente (A) | QGBT | ||||||||
| 2 | 3 | 4 | |||||||
| A | B | C | A | B | C | A | B | C | |
| h = 1 | 336,98 | 347,59 | 320,12 | 238,19 | 192,57 | 245,19 | 498,3 | 697,43 | 469,78 |
| h = 3 | 16,69 | 24,32 | 16,85 | 17,94 | 16,16 | 16,01 | 6,21 | 6,15 | 6,81 |
| h = 5 | 8,25 | 6,56 | 5,14 | 10,65 | 10,95 | 12,34 | 1,63 | 1,69 | 1,49 |
| h = 7 | 1,16 | 2,64 | 2,34 | 3,26 | 2,80 | 4,00 | 4,88 | 5,77 | 4,52 |
| h = 9 | 1,93 | 2,69 | 2,34 | 1,64 | 1,16 | 0,31 | 4,62 | 4,28 | 4,22 |
| h = 11 | 1,16 | 1,94 | 0,92 | 2,32 | 1,88 | 1,67 | 2,82 | 2,39 | 2,37 |
| h = 13 | 0,75 | 0,71 | 0,78 | 3,26 | 2,51 | 2,58 | 1,82 | 1,63 | 1,66 |
| h = 15 | 0,64 | 1,05 | 0,36 | 15,38 | 2,94 | 18,47 | 1,53 | 1,07 | 1,14 |
Fonte: elaboração própria.
A Tabela 9 apresenta o valor de pico das componentes harmônicas da corrente de neutro e o valor eficaz da corrente de neutro dos QGBTs, tal como foi feito para a planta sem o filtro (Tabela 6).
Tabela 9 – Valores de pico das componentes harmônicas da corrente de neutro e o valor eficaz da corrente de neutro dos QGBTs considerando a planta com o filtro
| Componente harmônica de corrente (A) | QGBT | ||
| 2 | 3 | 4 | |
| h = 1 | 52,2966 | 52,021 | 238,1714 |
| h = 3 | 57,7519 | 50,0857 | 19,1584 |
| h = 9 | 6,9532 | 3,1039 | 13,1321 |
| h = 15 | 2,0371 | 1,0794 | 3,681 |
| Valor eficaz da corrente (A) | 55,404 | 51,1287 | 169,2346 |
Fonte: elaboração própria.
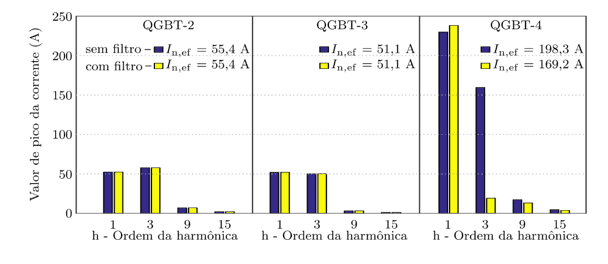
Ao comparar os resultados, é possível verificar que ao inserir o filtro houve uma redução do valor de pico das componentes de harmônicas da corrente de neutro do QGBT-4, com maior impacto na componente de ordem 3, alterando significativamente o valor eficaz da corrente de neutro neste QGBT.
Os resultados de simulação obtidos nessa seção e na seção anterior servem como base de dados para a análise comparativa apresentada na próxima seção.
6. RESULTADOS – ANÁLISE COMPARATIVA DOS DADOS OBTIDOS DA PLANTA COM E SEM O FILTRO
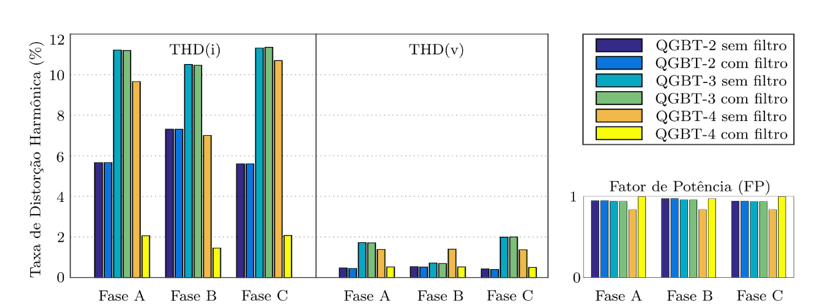
Para facilitar a análise comparativa dos resultados obtidos, a Figura 4 compara o valor das THD(i), THD(v) e FP para cada fase dos QGBTs da planta com e sem o filtro. É possível verificar que em todas as fases dos QGBT-2 e QGBT-3, não há uma mudança significativa nos valores de THD(i) da planta com e sem o filtro. No QGBT-4 confirmou-se uma diminuição significativa da THD(i) da planta com o filtro comparada com a planta sem o filtro. Em cada fase de todos os QGBTs das plantas com o filtro é visível uma diminuição das THD(v), se comparadas com as sem filtro. Apesar de todas as THD(v) reduzirem, o gráfico mostra que no QGBT-4 a redução é mais significativa. Em todas as fases do QGBT-4 da planta com o filtro houve um aumento no fator de potência, aproximando-se do valor unitário. Nos outros QGBTs, não houve mudança significativa nos valores do FP.
Figura 4 – Comparação das THD(i), THD(v) e FP de cada fase dos QGBTs da planta com e sem o filtro
Na Figura 5 é mostrada uma comparação dos valores das amplitudes das componentes harmônicas de corrente para cada QGBT. Após a inserção do filtro no QGBT-4, os valores das amplitudes desse diminuíram. Já nos QGBT-2 e QGBT-3 os valores permaneceram praticamente os mesmos.
Figura 5 – Comparação das amplitudes das componentes harmônicas das correntes de fase nos QGBTs da planta antes e após a inserção do filtro
Uma comparação das amplitudes das componentes harmônicas da corrente de neutro dos QGBTs é apresentada na Figura 6. Nos QGBT-2 e QGBT-3 não houve nenhuma alteração dessas componentes. Fica clara a redução dos valores das amplitudes após a inserção do filtro no QGBT-4, com exceção da componente fundamental (h = 1) que sofreu um aumento. Os valores eficazes das correntes de neutro nos QGBT-2 e QGBT-3 não variaram, mas no QGBT-4 o valor diminuiu.
Figura 6 – Comparação das amplitudes das componentes harmônicas da corrente de neutro nos QGBTs das plantas com e sem o filtro
Para verificar o desempenho do filtro foram comparados os valores obtidos com os valores recomendados pela IEEE Std 519-2014. Primeiramente calculam-se as correntes de curto-circuito (ISC) nos QGBTs e a corrente máxima solicitada pela carga (IL) na frequência fundamental. Admite-se que o valor eficaz da corrente medida no alimentador (Is) é igual ao valor de IL. O resultado final da faixa ISC/IL é apresentado na Tabela 10.
Tabela 10 – Parâmetro ISC/IL após a inserção do filtro na planta real
| QGBT | S (kVA) | VL (V) | VF (V) | Zpu (%) | Zbase (mΩ) | Ztrafo (mΩ) | ISC (kA) | IL (A) | ISC/IL |
| 2 | 500 | 380 | 220 | 5,83 | 288,8 | 16,84 | 13,07 | 238,65 | 54,75 |
| 246,45 | 53,02 | ||||||||
| 226,72 | 57,63 | ||||||||
| 3 | 500 | 380 | 220 | 7,30 | 288,8 | 21,08 | 10,44 | 169,46 | 61,58 |
| 136,91 | 76,22 | ||||||||
| 174,49 | 59,80 | ||||||||
| 4 | 500 | 380 | 220 | 7,30 | 288,8 | 21,08 | 10,44 | 352,42 | 29,61 |
| 493,21 | 21,16 | ||||||||
| 332,26 | 31,41 |
Fonte: elaboração própria.
Utilizando os dados da Tabela 8, calcula-se na Tabela 11 o maior valor percentual medido entre as harmônicas de cada faixa. Considera-se que, ao comparar com a recomendação da Tabela 1, os valores percentis no QGBT-2 e QGBT-3 devem ser avaliados para a faixa 50 < ISC/IL < 100 e que no QGBT-4 os limites devem ser avaliados para a faixa 20 < ISC/IL < 50.
Tabela 11 – Valores percentuais das componentes harmônicas das correntes e da TDD após a inserção do filtro
| QGBT | 3 ≤ h < 11 | 11 ≤ h < 17 | 17 ≤ h < 23 | 23 ≤ h < 35 | 35 ≤ h < 50 | TDD |
| 2 | 4,95% | 0,35% | 0% | 0% | 0% | 5,66% |
| 7,00% | 0,56% | 0% | 0% | 0% | 7,31% | |
| 5,26% | 0,29% | 0% | 0% | 0% | 5,60% | |
| 3 | 7,94% | 1,03% | 0% | 0% | 0% | 11,19% |
| 8,39% | 0,98% | 0% | 0% | 0% | 10,46% | |
| 6,53% | 0,68% | 0% | 0% | 0% | 11,35% | |
| 4 | 1,25% | 0,57% | 0% | 0% | 0% | 2,06% |
| 0,88% | 0,34% | 0% | 0% | 0% | 1,45% | |
| 1,45% | 0,50% | 0% | 0% | 0% | 2,07% |
Fonte: elaboração própria.
Por meio da comparação com a Tabela 1, verifica-se que em todos os QGBTs os limites recomendados pela IEEE Std 519-2014 são respeitados e que a inserção do filtro se mostra eficaz no sentido de atender a recomendação desta norma.
7. CONCLUSÃO
Por intermédio de análises realizadas ao longo do estudo, assim como pelas comparações dos valores obtidos, pode-se afirmar que o filtro modelado para as harmônicas de ordem três e cinco apresentaram um bom desempenho. Na planta real com o filtro, em todas as fases do QGBT-4, houve um aumento no fator de potência, aproximando-o do valor unitário. Nos QGBT-2 e QGBT-3 não houve mudanças significativas, o que era esperado, pois não foram inseridos filtros nos mesmos. A questão norteadora é respondida, uma vez que a eficiência do filtro pode ser comprovada ao comparar os resultados obtidos com os limites recomendados pela IEEE Std. 519-2014, mostrando que o filtro modelado atende aos limites dos valores percentuais das componentes harmônicas das correntes e da TDD. Com isso, o trabalho atinge o seu objetivo principal do estudo de caso: projetar um filtro passivo com o desempenho desejado.
REFERÊNCIAS
ANEEL, Procedimentos de Distribuição de Energia Elétrica no Sistema Elétrico Nacional – PRODIST Módulo 8 – Qualidade da Energia Elétrica, Rev. 10, http://www.aneel.gov.br/modulo-8, 2017.
DUPCZAK, Bruno S. et al. Avaliação de Distorções Harmônicas e Desequilíbrios de Tensão e de Corrente na Subestação do IFSC Câmpus Florianópolis. Florianópolis, 2018.
IEEE, Recommended practice and requirements for harmonic control in electric power systems, IEEE Std 519-2014 (Revision of IEEE Std 519-1992) – Redline, pp. 1–213, June 2014.
INSTITUTO BRASILEIRO DO COBRE (PROCOBRE); SCHNEIDER ELECTRIC. Workshop Instalações Elétricas de Baixa Tensão: Qualidade de Energia, Harmônicas. Disponível em: <https://www.se.com/br/pt/work/services/training/apostilas.jsp>. Acesso em: 6 out. 2018.
KASSICK, E. V. Harmônicas em sistemas elétricos de baixa tensão. 2016. 134 f. Apostila – Faculdade de Engenharia Elétrica, Instituto Federal de Educação, 2016.
QUADROS, Marco Aurélio. Filtragem Passiva de Harmônicas em Instalações Elétricas. 1999. 143 f. Dissertação (Mestrado) – Curso de Engenharia Elétrica, Universidade Federal de Santa Catarina, Florianópolis, 1999. Disponível em: <https://repositorio.ufsc.br/handle/123456789/80832>. Acesso em: 6 out. 2018.
TEODORO, Diogo. Estudo Sobre a Utilização de Filtros Passivos para Redução de Conteúdo Harmônico nas Instalações Elétricas do IFSC – Câmpus Florianópolis. 2019. 155 f. TCC (Graduação) – Curso de Engenharia Elétrica, Instituto Federal de Santa Catarina, Florianópolis, 2019.
[1] Engenheira Eletricista pelo Instituto Federal de Santa Catarina – IFSC. ORCID: 0000-0002-9398-850X.
[2] Doutora em Engenharia Elétrica pela Universidade Federal de Santa Catarina, Mestre em Engenharia Elétrica pela Universidade Federal de Santa Catarina, Bacharel em Engenharia Elétrica pela Universidade Federal de Santa Catarina. ORCID: 0000-0003-3708-9582.
[3] Doutor em Engenharia Elétrica pela Universidade Federal de Santa Catarina, Mestre em Engenharia Elétrica pela Universidade Federal de Santa Catarina, Bacharel em Engenharia Elétrica pela Universidade Federal de Santa Maria. ORCID: 0000-0003-2219-6836.
Enviado: Junho, 2022.
Aprovado: Outubro, 2022.