ARTIGO ORIGINAL
SANTANA, Danilo Fernandes [1]
SANTANA, Danilo Fernandes. Comparação entre estruturas e fundações dimensionadas automaticamente por software e métodos de cálculos tradicionais. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 10, Vol. 02, pp. 138-175. Outubro de 2019. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/estruturas-e-fundacoes
RESUMO
O presente artigo trata do assunto dimensionamento estrutural com foco em estruturas de concreto armado. Será feita a comparação entre resultados adquiridos com o uso de software de cálculo estrutural e métodos matemáticos utilizados no ensino superior acadêmico. O software utilizado é o CypeCAD que utiliza para dimensionamento o método dos deslocamentos com formulação matricial de pórtico espacial. O cálculo de peças isoladas apresenta uma maior profundidade de análise, mas atualmente a velocidade em que são dimensionadas as estruturas pelos programas estimula o dimensionamento por cálculos manuais apenas para conferência de alguns resultados obtidos pelos softwares. O objetivo do trabalho é expor a diferença de resultados encontrados por cálculos manuais matemáticos e softwares. Será apresentado um projeto arquitetônico de domínio público e feito o dimensionamento estrutural de vigas, pilares, sapatas e lajes.
Palavras-chave: Dimensionamento estrutural, Software de cálculo estrutural, Cypecad, dimensionamento de vigas, pilares.
1. INTRODUÇÃO
Profissionais de Engenharia Civil projetistas de estruturas devem dominar a teoria e os métodos de cálculo estrutural aprendidos no ensino superior. Não se pode negligenciar o conhecimento adquirido em métodos tradicionais, pois a responsabilidade da estabilidade da estrutura de concreto é do Engenheiro civil. Se algum problema ocorrer com a estrutura, o engenheiro precisa provar que seus cálculos estão corretos, com isso, é necessário pelo menos entender os cálculos feitos por softwares.
Atualmente programas de cálculo estrutural são utilizados por praticamente todos os escritórios de projetos. Eles dão agilidade à produção e seguem normas estabelecidas na Engenharia Civil. Mas a facilidade em utilizar os programas fez com que profissionais começassem a gerar projetos confiando totalmente nas pranchas geradas. O cálculo de estruturas de concreto armado passou a ser feito até por desenhistas e o custo do projeto estrutural também diminuiu no mercado, devido ao aumento de profissionais capazes de utilizar as ferramentas.
Serão utilizados métodos tradicionais de cálculo para comparar com aqueles adquiridos através do cálculo de software de estruturas e vamos verificar a semelhança entre resultados.
2. PROJETO ARQUITETÔNICO
O trabalho será feito a partir de um projeto arquitetônico de uma obra real para trazer resultados próximos a rotina de projetistas. Trata-se de uma obra com fim social que melhora as condições de higiene e saúde de famílias de baixa renda. Os projetos estão disponibilizados no site da FUNASA. Abaixo temos a Figura 1 que representa a planta baixa da construção e a Figura 2 que apresenta um corte e uma fachada do projeto.
Figura 1. Planta baixa do projeto arquitetônico.
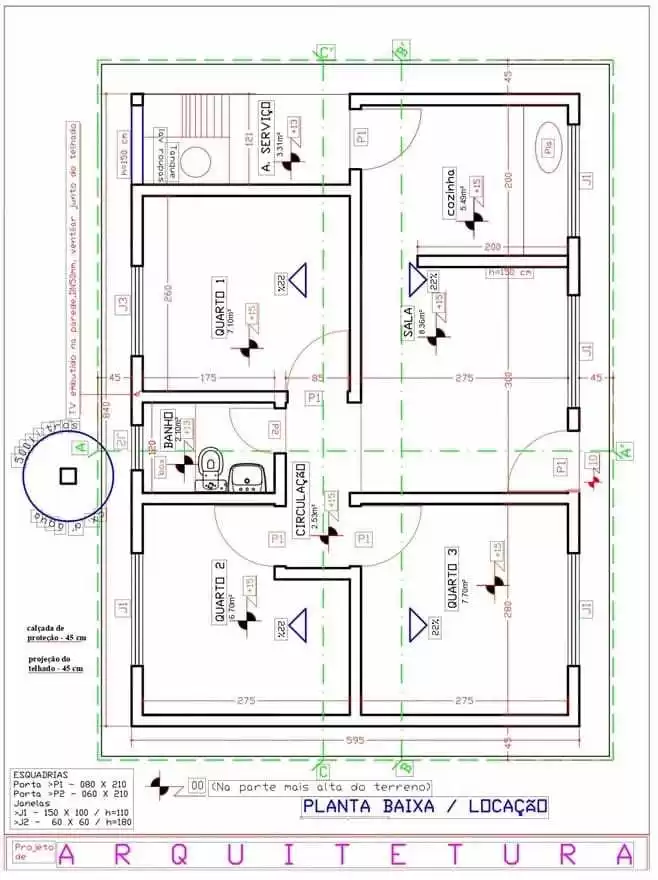
Figura 2. Corte e Fachada Lateral.
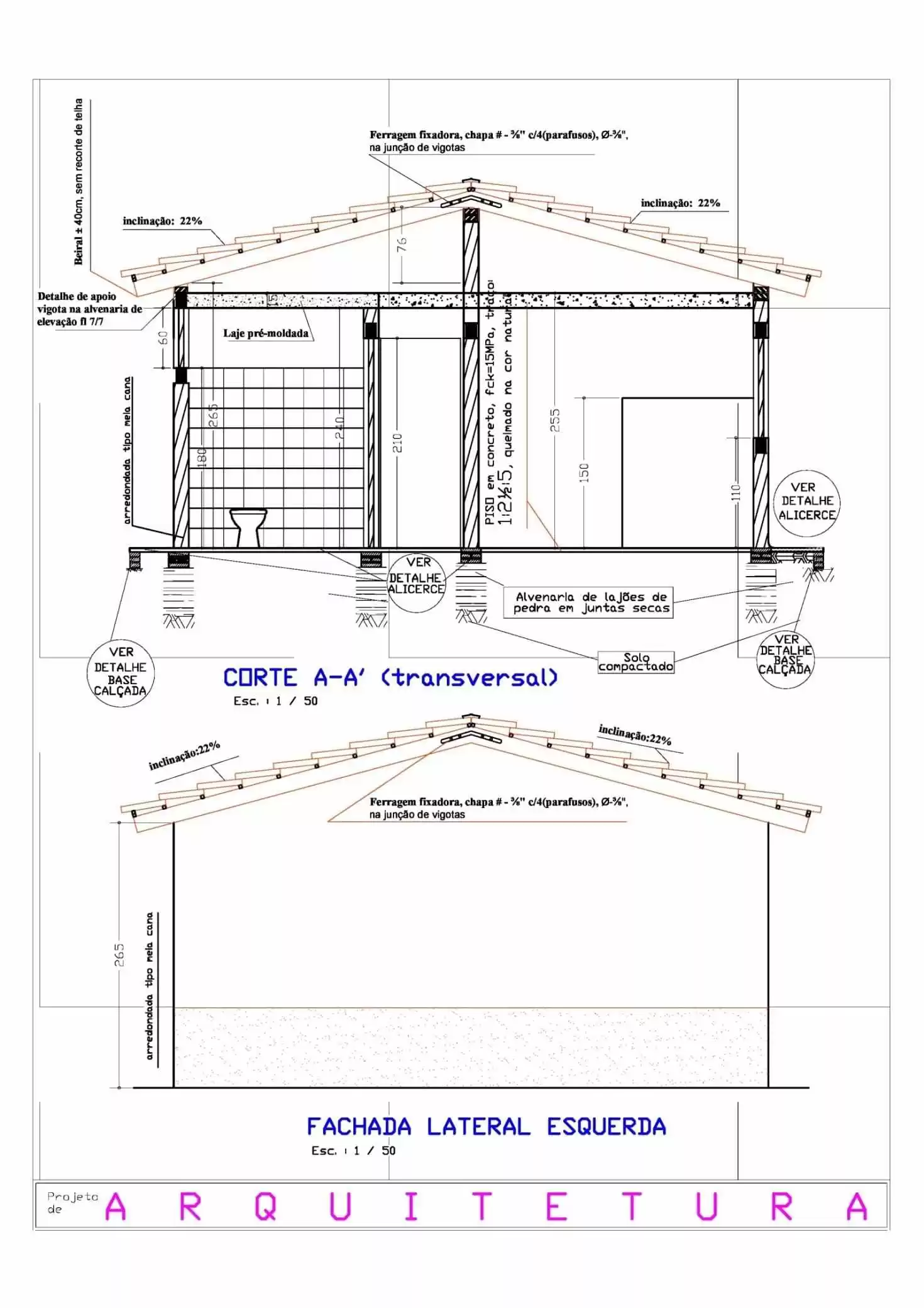
3. DADOS INICIAIS DE CÁLCULO
É necessário adotar algumas características para serem utilizadas ao longo dos cálculos de projeto. Utilizaremos o concreto C-20, por ser uma obra de pequeno porte. O aço para as armaduras das estruturas de concreto será o CA-50. Adotamos ainda um solo de argila dura que tem resistência de 0,245 Mpa.
4. MEDIDAS DE PILARES E SAPATAS
As medidas mínimas dos pilares são determinadas pela Norma NBR 6118. A dimensão mínima é de 19 cm, mas existem casos especiais em que podem ser aceitos medidas de até 14 cm. Isso exige a multiplicação por um coeficiente adicional γn que é apresentado na tabela 1. Em todos os casos não são permitidos pilares com seção transversal de área inferior a 360 cm².
Tabela 1 Coeficiente γ para pilares com dimensão menor que 19 cm.
| b cm | >=19 | 18 | 17 | 16 | 15 | 14 |
| Γn | 1,00 | 1,05 | 1,10 | 1,15 | 1,20 | 1,25 |
Fonte: NBR 6118.
Além disso, as melhores medidas dos pilares para obras são aquelas em que é possível embuti-los na parede, assim as medidas dos pilares do projeto deste trabalho podem ser de 15x25cm que são números inteiros.
As medidas mínimas das laterais da sapata são de 60 cm e sua profundidade de 150 cm, exceto com dimensões inferiores a 1 metro, cuja profundidade pode ser reduzida. No projeto deste artigo deixaremos aberto ao software indicar as medidas necessárias e no momento do cálculo manual, verificamos as medidas.
5. MEDIDAS DE VIGAS E LAJES
De acordo com a NBR 6118 as medidas mínimas da viga são 12 cm de largura, com exceção de alguns casos especiais que permitem até 10 cm e a altura é resultado da fórmula abaixo, considerando o mínimo possível de 25 cm. Para facilitar a execução existe ainda um arredondamento do valor encontrado na resolução da fórmula.
Figura 3. Valores práticos para estimativa de altura de vigas.
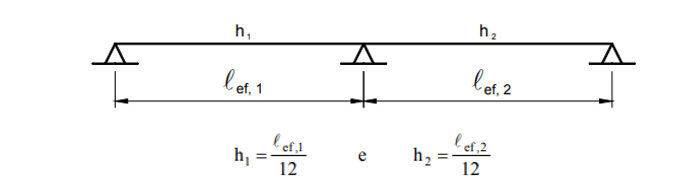
No projeto utiliza-se a altura da viga de 30 cm, encontrada através da fórmula acima e largura de 15 cm que é a mesma largura do pilar.
A altura da laje maciça também é definida na norma NBR 6118 e está indicada nos itens abaixo, sendo relacionada com a sua função:
a) 7 cm para lajes de cobertura não em balanço;
b) 8 cm para lajes de piso não em balanço;
c) 10 cm para lajes em balanço;
d) 10 cm para lajes que suportem veículos de peso total menor ou igual à 30 kN;
e) 12 cm para lajes que suportem veículos de peso total maior que 30 kN;
f) 15 cm para lajes com protensão apoiadas em vigas, l/42 para lajes de piso biapoiadas e l/50 para lajes de piso contínuas;
g) 16 cm para lajes lisas e 14 cm para lajes-cogumelo.
No projeto deste trabalho utilizamos 10 cm de altura para as lajes.
6. LOCAÇÃO DE PILARES E SAPATAS
Em obras civis busca-se embutir os pilares nas paredes e para facilidade de execução não variar muito as dimensões dos mesmos. De acordo com premissas descritas no item 4, adotaremos pilares de 15x25cm. A locação está na figura 4.
As sapatas são locadas abaixo dos pilares, pois são bases para os mesmos. As medidas adotadas pelo software Cypecad foram 85×85 cm. Esse valor será verificado por outro método de cálculo. A locação das sapatas está na figura 5.
Figura 4. Locação de pilares .
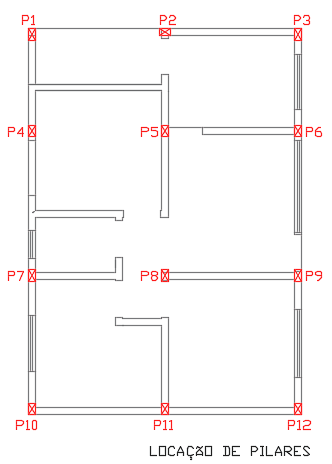
Figura 5. Locação de Sapatas.
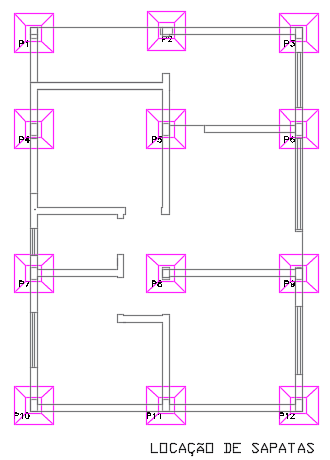
7. LOCAÇÃO DE VIGAS E LAJES
As vigas são apoios para as lajes e nesse projeto terão medidas de 15x30cm. Estão locadas conforme a figura 6. E as lajes maciças tem 10 cm de altura e estão representadas na figura 7.
Figura 6. Locação das vigas.
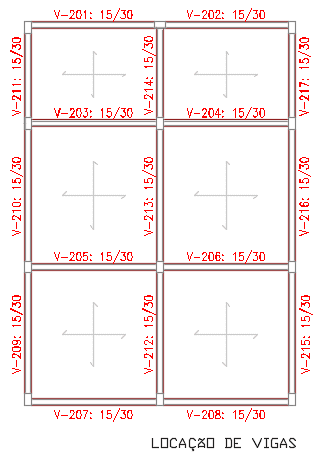
Figura 7. Locação das lajes.
8. DIMENSIONAMENTO DE PILARES NO SOFTWARE
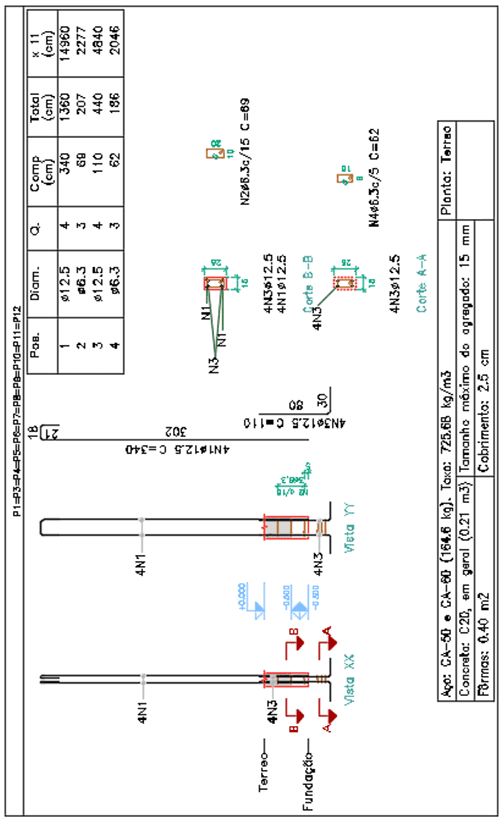
Foram dimensionadas armaduras longitudinais com diâmetro de 12.5 cm e estribos com 6.3 cm. Armaduras com menores espessuras serão verificadas através de métodos tradicionais de cálculo no item 13 deste trabalho. Na figura 8 temos o projeto estrutural dos pilares e quantitativo de aços gerados pelo software.
Figura 8. Projeto estrutural de pilares.
9. DIMENSIONAMENTO DE VIGAS NO SOFTWARE
Temos no projeto as vigas baldrames e vigas do térreo. Utilizaremos a viga 203 do térreo como estudo de caso, pois é uma viga mais próxima ao centro da estrutura e recebe uma carga maior que outras vigas laterais. Na figura 9 temos a planta para a localização da viga indicada.
Figura 9. Planta de locação de vigas.
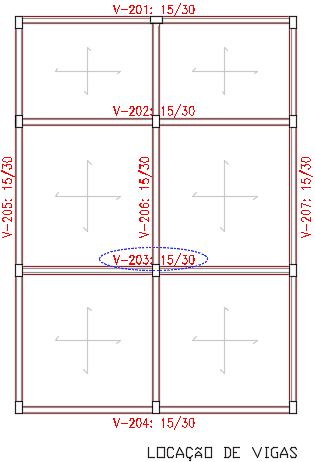
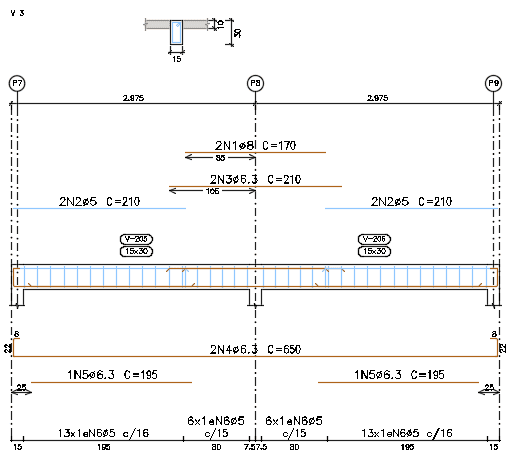
Abaixo temos o dimensionamento da viga 203 com aços de diâmetro 8, 6.3 e 5 sugerido pelo software:
Figura 10. Projeto estrutural da viga 203.
10. DIMENSIONAMENTO DE LAJES NO SOFTWARE
As lajes maciças são compostas de armaduras superiores e inferiores. Na figura abaixo temos a indicação da laje 3 que será verificada neste trabalho. Nas figuras seguintes estão as 4 plantas de armaduras da laje geradas pelo software CypeCad.
Figura 11. Locação das lajes.
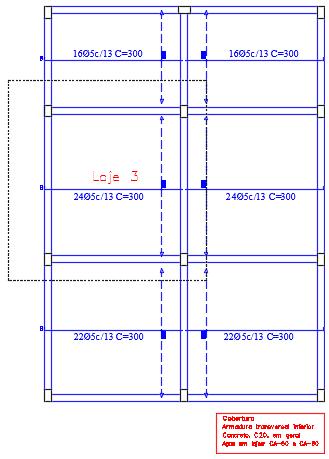
Figura 12. Armadura Transversa inferior da Laje 3.
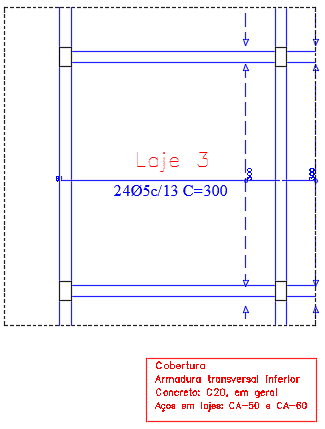
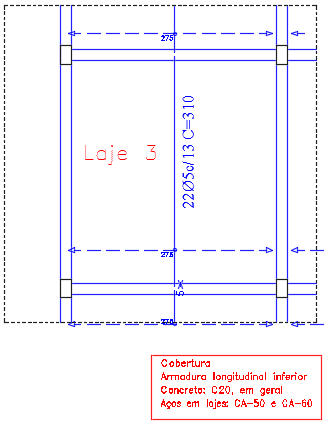
Figura 13. Armadura Longitudinal inferior da Laje 3.
Figura 14. Armadura Transversal Superior da Laje 3.
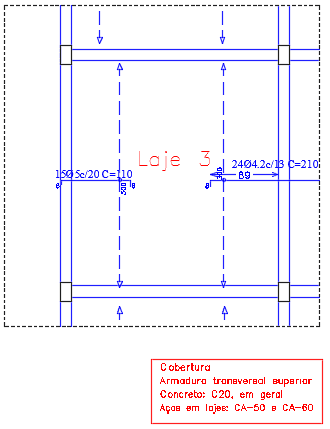
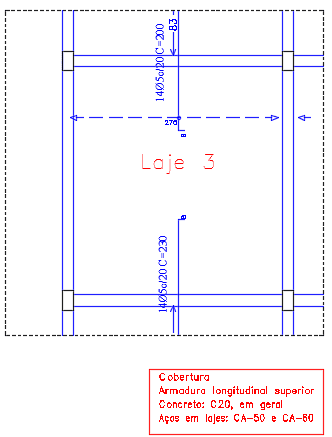
Figura 15. Armadura Longitudinal Superior da Laje 3.
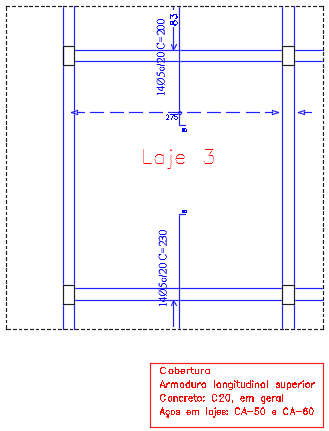
11. DIMENSIONAMENTO DE SAPATAS NO SOFTWARE
Todas as sapatas foram dimensionadas iguais com tamanho de 85×85 cm e armaduras com aço de 10 cm de diâmetro. Na verificação manual utilizaremos medidas e aços com menores tamanhos.
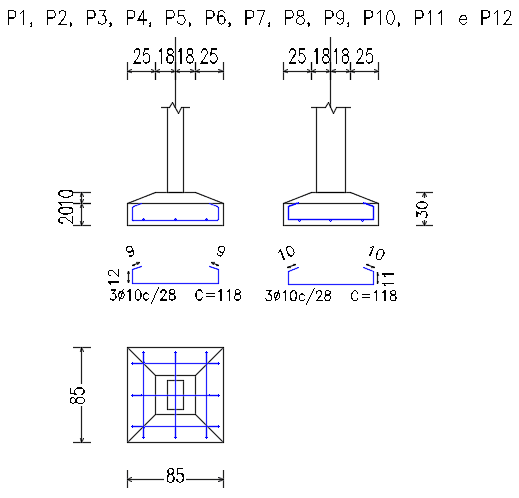
Figura 16. Projeto estrutural da sapata.
12. CÁLCULO MANUAL DO PILAR
O pilar a ser dimensionado será o P8, indicado na figura do item 6.
Figura 17. Variáveis do pilar.
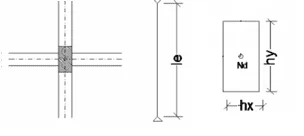
O método de cálculo será do pilar padrão de curvatura aproximada.
Roteiro de Cálculo P8:
Temos a força Normal que foi retirada do software Cypecad => Nk = 92,2 kN,
A altura útil do pilar le = 245 cm
hx = 15 cm
hy = 25 cm
Área de concreto => Ac = hy * hx = 375 cm²
O coeficiente γn é exposto na NBR618 e item 4 na figura 3, devido a dimensão do pilar menor que 19 cm.
γn = 1,20
Coeficiente de ponderação do concreto => γf = 1,40
Resistência do concreto => fck = ![]()
Resistência de escoamento do aço => fyk = ![]()
Cobrimento do pilar d’x = 2,5 cm,
Coeficiente do pilar αb = 1
a) Esforços solicitantes do pilar
Nd = γn * γf * Nk = 1,20 * 1,40 * 92,2 = 154 kN
b) Índice de esbeltez
λx = 3,46 * le / hx = 3,46 * 245 / 15 = 56,51
λy = 3,46 * le / hx = 3,46 * 245 / 25 = 33,91
c) Momentos mínimos
M1d.min.x = Nd * (1,5 + 0,03 * hx) = 154 * (1,5 + 0,03 * 15) = 300,30 kN.cm
M1d.min.y = Nd * (1,5 + 0,03 * hy) = 154 * (1,5 + 0,03 * 25) = 346,50 kN.cm
d) Excentricidades
el.min.x = M1d.min.x / Nd = 300,3 / 154 = 1,95 cm
el.min.y = M1d.min.y / Nd = 346,5 / 154 = 2,25 cm
e) Momento de segunda ordem
Aplicação de efeito de 2ª ordem para x, pois tem índice de esbeltez maior que 35.
Força Normal Adimensional (v) = Nd / (Ac *fcd) = 154 / ( 375 * 1,428 ) = 0,287
Raio de giração (r) = 0,005 / (hx * (v +0,5)) = 4,23 x 10-4 cm
Excentricidade de segunda ordem (e2x) = (le² / 10) * r = (245² / 10) * 4,23 x 10-4 = 2,54 cm
f) Momento total
Md.tot.x = αb * M1d.min.x + Nd * e2x = (1 * 300,3) + (154 * 2,54) = 691,46 kN.cm
Cálculo do µ a ser utilizado no ábaco de Venturini:
µx = Md.tot.x / (hx * Ac * fcd) = 691,46 / (15 * 375 * 1,428) = 0,086
µy = M1d.min.y / (hy * Ac * fcd) = 346,5 / (25 * 375 * 1,428) = 0,026
Cálculo d’x/ hx e d’y/ hy para escolher qual ábaco de Venturini utilizar:
d’x/ hx = 2,5 / 15 = 0,166
d’x/ hy = 2,5 / 25 = 0,10
No eixo x está a menor inércia e a armadura encontrada em relação a este eixo é maior que y, então adota-se o cálculo em relação a x para dimensionar a armadura. O ábaco de Venturini a ser considerado está abaixo:
Figura 18. Ábaco de Venturini.
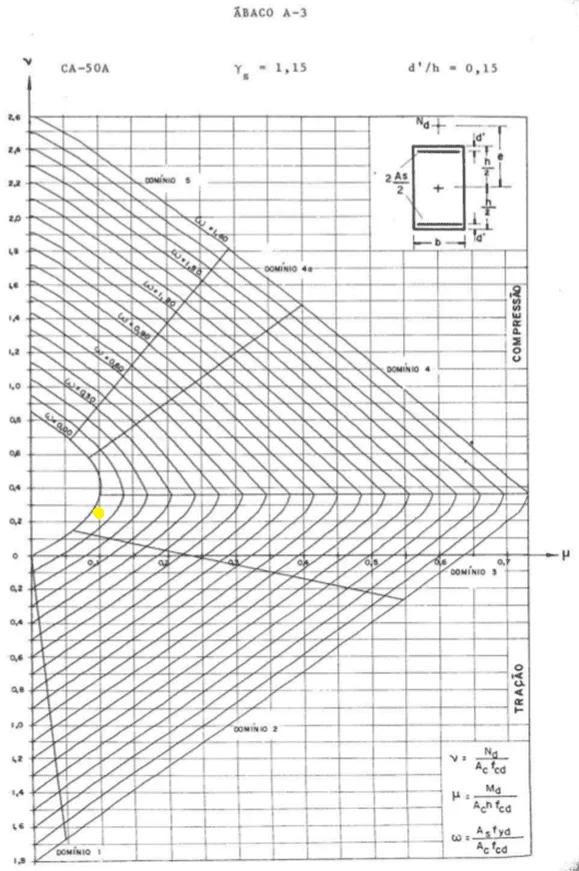
Os dados encontrados de v e µ são respectivamente 0,287 e 0,086.
Com isso, o w encontrado no ábaco está marcado em amarelo e tem valor aproximado de 0,002.
A área de aço calculada foi baixa por causa das baixas cargas no pilar, mas existe uma fórmula que define a área mínima de aço de pilares:
– As.mín = 0,004 * hx * hy = 0,004 * 15 * 25 = 1,5 cm²
A espessura das barras é encontrada na tabela abaixo a partir de As.
Tabela 2. Área de aço da seção conforme número de barras.
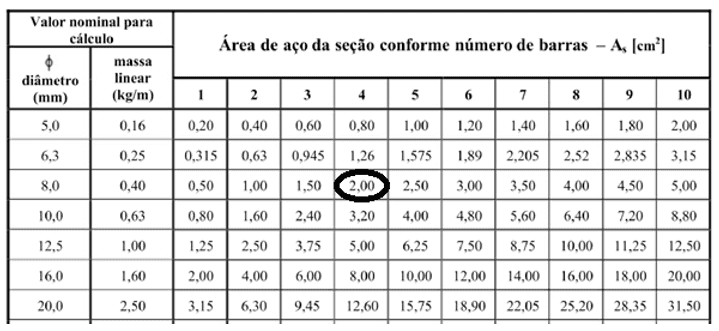
Encontra-se 4 barras de 8 mm para As = 1,5. Mas a norma NBR 6118 exige que a armadura longitudinal do pilar seja de 10 mm.
Então o resultado do cálculo são 4 barras de 10 mm na direção longitudinal.
A seguir calcula-se a os estribos do pilar.
As condicionais são 2:
– Mínimo de 5mm;
– Mínimo de diâmetro da armadura longitudinal / 4 = 10/4 =2,5.
Então tem-se o estribo = 5 mm.
O espaçamento tem 3 condicionais:
– Menor ou igual 20 cm;
– Igual a menor dimensão do pilar = 15 cm;
– Menor ou igual 12 * diâmetro da armadura longitudinal em cm= 12 * 1 = 12 cm
Então o espaçamento do estribo é de 12 cm.
13. CÁLCULO MANUAL DA VIGA
A viga a ser dimensionada é a 203, indicada no item 9.
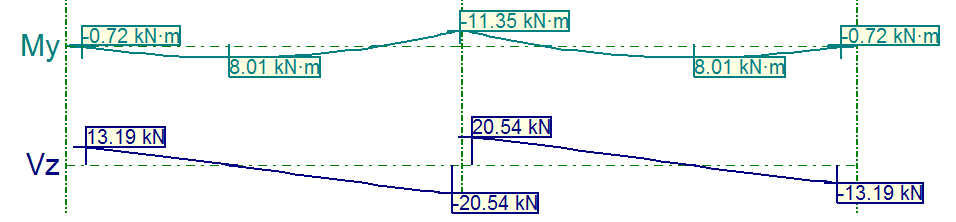
As cargas foram retiradas do software, primeiro o diagrama de momentos fletores e depois o diagrama de forças cortantes.
Figura 19. Diagrama de Momentos Fletores e Forças Cortantes da Viga.
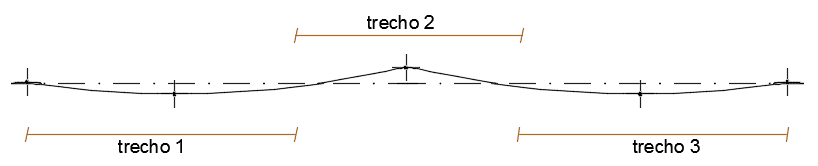
bw = hx = 15 cm
h = 30 cm
fck = 20 Mpa
d = h – cobrimento = 30 – 3 = 27 cm
Momentos ao longo da viga:
No trecho 1 e 3: Msk1 = Msk3 = 8,01 kN.m
Msd1 e Msd3 = Msk * 1,4 * 100 = 1.121,40 kN.cm
No trecho 2: Msk2 = 11,35 kN.m
Msd2 = Msk2 * 1,4 * 100 = 1.589 kN.cm
Forças cortantes nos 3 trechos da viga:
Vsk1 = 13,19 kN
Vsk2 = 20,54 kN
Vsk3 = 13,19 kN
Armadura longitudinal no trecho 1 e 3:
Kc = (bw * d²) / Msd1 = (15 * 27²) / 1.121,4 = 9,75
Armadura longitudinal no trecho 2:
Kc = (bw * d²) / Msd2 = (15 * 27²) / 1.589 = 6,88
Utiliza-se a tabela abaixo para encontrar o Ks:
Tabela 3. Tabela de coeficiente Kc e Ks.
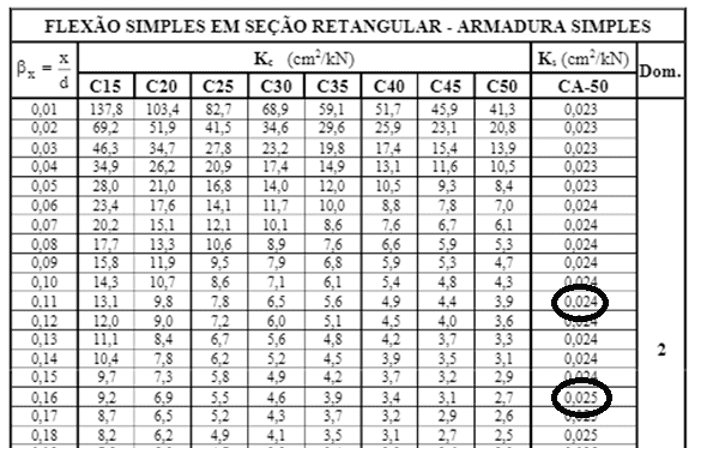
Ks1 = 0,024;
Ks2 = 0,025.
As1 e As3= (Ks1 * Msd1) / d = (0,024 * 1.121,4) / 27 = 1 cm²
As2 = (Ks2 * Msd2) / d = (0,025 * 1.589) / 27 = 1,47 cm²
Tabela 4. Área de aço da seção conforme número de barras.
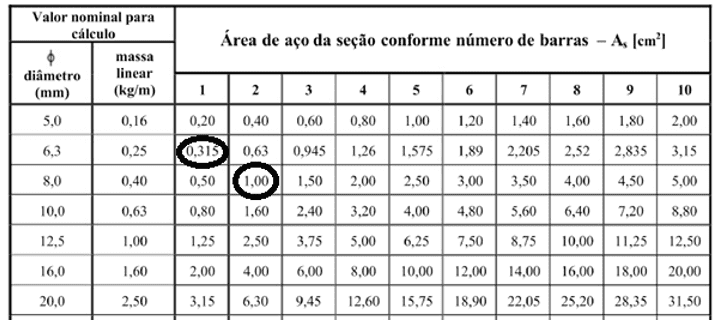
2 barras de 8 mm atendem a área necessária do trecho 1.
Armadura no trecho 3 é igual armadura no trecho 1, então tem-se 2 barras de 8 mm.
No trecho 2, temos 2 barras de 8 mm e 1 barra de 6.3 mm.
Dimensionamento de estribos
Coeficiente considerado para do concreto
Resistência característica do concreto 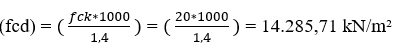
Força cortante resistente de cálculo
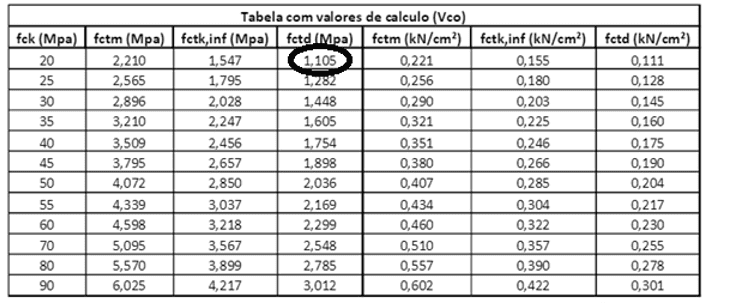
O valor do coeficiente relacionado a resistência do concreto (fctd) para 20 Mpa, encontrado na tabela abaixo é 1.105 kN/m²
Tabela 5. Tabela com valores de cálculo (Vco)
Resistência do concreto a força cortante
Utilizaremos o Vsk2, pois é a maior força cortante na viga.
Força absorvida pela armadura transversal
(Vsw2) = Vsk2 * 1,4 – Vc = 20,54 * 1,4 – 26,82 = 1,936 kN
Resistência do aço (fyd) = 50 / 1,15 = 43,478
Armadura do estribo
Utilizaremos o Asw.min para encontrarmos os diâmetros das barras de aço do estribo.
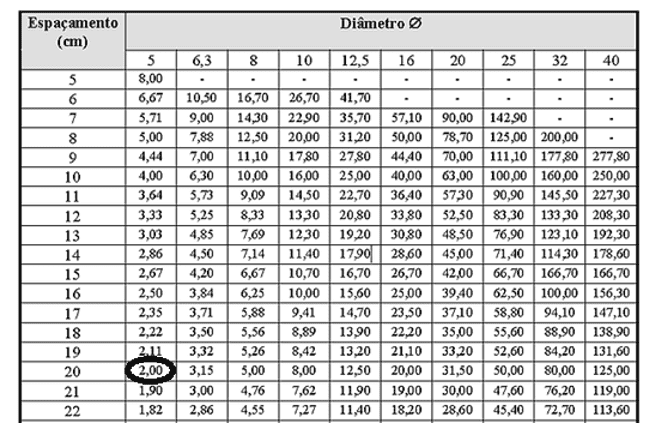
De acordo com a tabela abaixo, temos estribos de 5 mm com espaçamento máximo de 22cm, então podemos arredondar para 20 cm.
O resultado dos estribos são barras de 5mm a cada 20 cm.
Tabela 6. Área de estribos de 2 ramos por unidade de comprimento
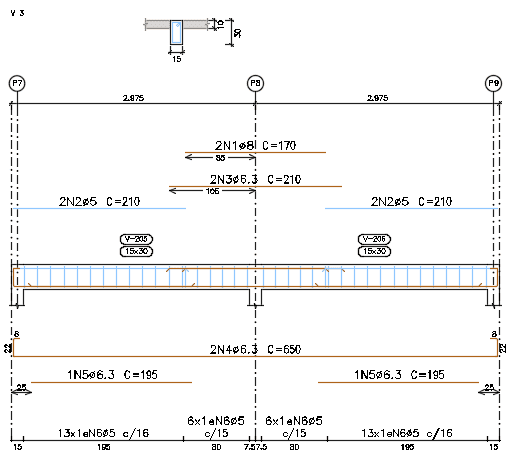
Novo dimensionamento:
Figura 20. Projeto estrutural da viga.
14. CÁLCULO MANUAL DA LAJE
O método de cálculo utilizado para a laje será através das tabelas de Czerny.
Laje 3
Figura 21. Projeto estrutural da laje.
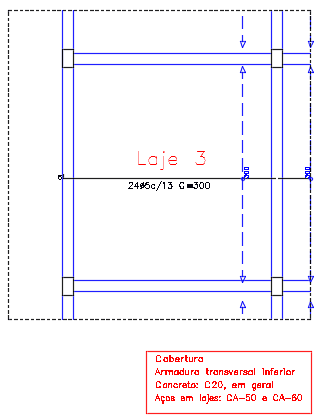
Vão da laje em x = 275 cm
Vão da laje em y = 300 cm
Sobrecarga de acordo com a Norma 6120 = 0,150 tf/ m²
Carga Permanente adotada = 0,100 tf/m²
Espessura = 10 cm
Cobrimento = 2,5 cm
fck = 20 Mpa; fyk = 500 Mpa
Peso próprio = espessura * 2,5 / 100 = 10 * 2,5 / 100 = 0,250 tf/m²
Carga total = Peso próprio + Sobrecarga + Carga Permanente = 0,250 + 0,150 + 0,100 = 0,500 tf/m²
Resistência do concreto majorada (Ocd) = fck / (1,4 * 0,85) /100 = 0,168 tf/cm²
fyd = fyk / 1,15 / 100 = 4,348 tf/cm²
ly / lx = 300 / 275 = 1,091
A tabela de Czerny a ser utilizada para a laje escolhida é referente a 3 bordas engastadas.
Tabela 7. Tabela de Czerny
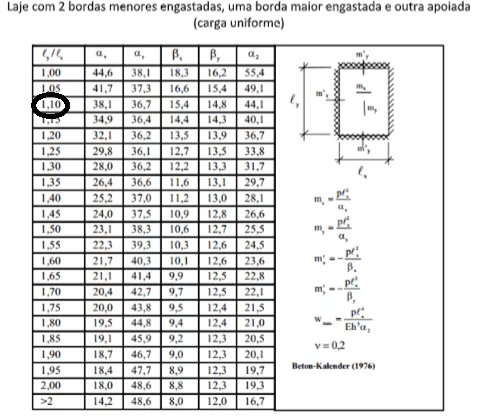
O ly / lx utilizado da tabela será 1,10, pois é o mais próximo do valor calculado.
Módulo de elasticidade
Inércia da Laje = (100 * espessura³ ) / 12 = (100 * 10³) / 12 = 8.333,333 cm4/m
Flecha = (Carga total / 100) * (lx4 / E) / Inércia da Laje / y
Flecha = (0,500 / 100) * (2754 / 212,873) / 8.333,33 / 44,1 = 0,365cm
Flecha máxima = lx / 250 = 275 / 250 = 1,1cm
A flecha calculada é menor que a flecha máxima, então pode-se manter a laje com 10 cm de altura.
Os próximos cálculos serão feitos através de uma tabela e as fórmulas utilizadas serão apresentadas abaixo.
| αx | Αy | βx | βy | y | |
| Dados base | 38.100 | 36.700 | 15.400 | 14.800 | 44.100 |
| Momento fletor | 0.099 | 0.103 | 0.245 | 0.255 | |
| Diâmetro da barra | 5.000 | 5.000 | 5.000 | 5.000 | |
| d | 7.250 | 7.250 | 7.250 | 7.250 | |
| µ | 0.016 | 0.016 | 0.039 | 0.040 | |
| ɛ | 0.016 | 0.016 | 0.040 | 0.041 | |
| As | 1.500 | 1.500 | 1.500 | 1.500 | |
| As barra | 0.196 | 0.196 | 0.196 | 0.196 | |
| Espaçamento | 13.000 | 13.000 | 13.000 | 13.000 |
Momento fletor = ( P * l²) / αx;
Diâmetro da barra = valor adotado;
d = espessura da laje – cobrimento – diâmetro da barra / espessura da laje / 2;
µ = Momento fletor * 1,4 / d² / Ocd;
ɛ = 1 – (1 – 2 * µ)0,5
As = ɛ * 100 * d * Ocd ou As = Espessura da laje * 100 * 0,0015
As barra = diâmetro da barra² * π / 4 /100
Foram encontradas armaduras de 5 mm com espaçamento de 13 cm.
Figura 22. Armadura Transversal Inferior da Laje 3
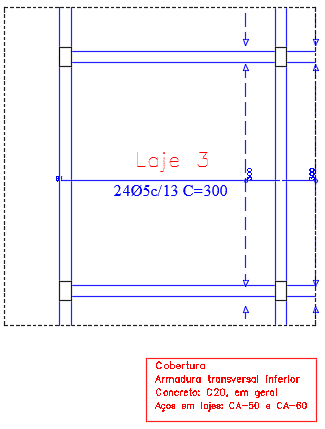
Figura 23. Armadura Longitudinal Inferior da Laje 3
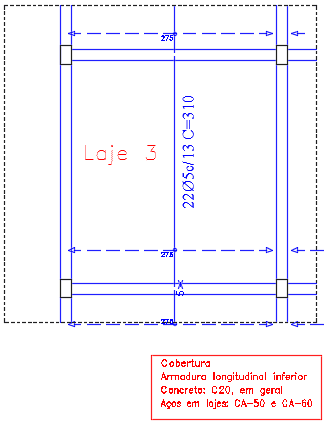
Armadura negativa em x
Cortante máxima = lx * Carga total * 0,65 = 2,75 * 0,500 * 0,65 = 0,890tf/m
Cálculo em Newtons Msx = 8,9kN/cm
Msdx = Msx * 1,4 * 100 = 1.246
Kc = (bw * d²) / Msdx = (100 * 7,5²) / 1.246 = 4,51
Ks encontrado na tabela 3 = 0,026
As = (Ks * Msdx) / d = (0,026 * 1.246) / 7,5 = 4,32
Adotando-se barras de 5mm:
Espaçamento (S) = As / Abarra = 4,32 / 0,20 = 21,6 ou arredonda-se para 20.
Armadura negativa em y
Cortante máxima = ly * Carga total * 0,65 = 3,00 * 0,500 * 0,65 = 0,975tf/m
Cálculo em Newtons Msx = 9,75kN/cm
Msdx = Msx * 1,4 * 100 = 1.365
Kc = (bw * d²) / Msdx = (100 * 7,5²) / 1.365 = 4,121
Ks encontrado na tabela 3 = 0,026
As = (Ks * Msdx) / d = (0,026 * 1.365) / 7,5 = 4,732
Adotando-se barras de 5mm:
Espaçamento (S) = As / Abarra = 4,732 / 0,20 = 23,66 ou arredonda-se para 20.
Figura 24. Armadura Transversal Superior da Laje 3.
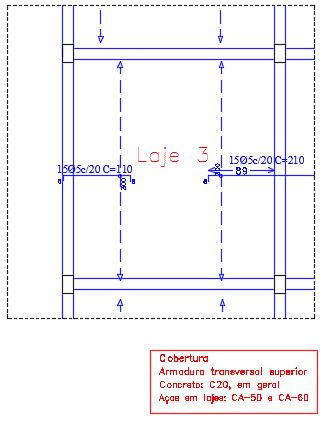
Figura 25. Armadura Longitudinal Superior da Laje 3.
15. CÁLCULO MANUAL DA SAPATA
Figura 26. Variáveis da sapata
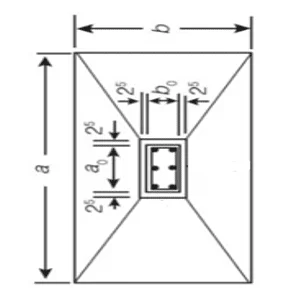
O método de cálculo para a sapata será o CEB70.
A sapata dimensionada será a S8 do projeto, referente ao pilar P8.
Nk = 92,2 kN
Maior seção do pilar (ap) = 25 cm
Menor seção do pilar (bp) = 15 cm
fyd = 50 / 1,15 = 43,478
diâmetro do aço do pilar = 10 mm
Fator de majoração do peso próprio da sapata Kmaj = 1,05
Tensão admissível do solo (σ adm) = 0,245 Mpa ou 0,0245 kN/cm²
fck = 20 Mpa
fcd = fck / 10 / 1,4 = 1,428 kN/cm²
Área da sapata (Ssap) = Kmaj * Nk / σ adm = 1,05 * 92,2 / 0,0245 = 3951,428 cm²
Cálculo das tensões na base da Sapata
σmáx = (Kmaj * Nk / (a * b)) * (1 + (6 * e / a)) = (1,05 * 92,2 / (70 * 60)) * (1 + (6 * 1 / 70)) = 0,025kN/cm²
σadm > σmáx = 1 (Se 1, ok, se 0 redimensionar).
A σmáx foi maior que a tensão admissível do solo, então adotaremos novas medidas para a sapata, sendo a = 75cm e b = 65cm.
σmáx = (Kmaj * Nk / (a * b)) * (1 + (6 * e / a)) = (1,05 * 92,2 / (75 * 65)) * (1 + (6 * 1 / 75)) = 0,021kN/cm²
Medidas da sapata finais são a = 75cm e b = 65cm.
Altura da sapata (h) = (a – ap) / 3 = (75 – 25) / 3 = 16,67 cm
Comprimento de ancoragem do pilar (lb) com gancho encontrado na tabela abaixo = 31cm
A altura da sapata precisa ser maior que o comprimento de ancoragem do pilar, então podemos escolher a altura da sapata = 35 cm.
Tabela 8. Tabela de comprimento de ancoragem
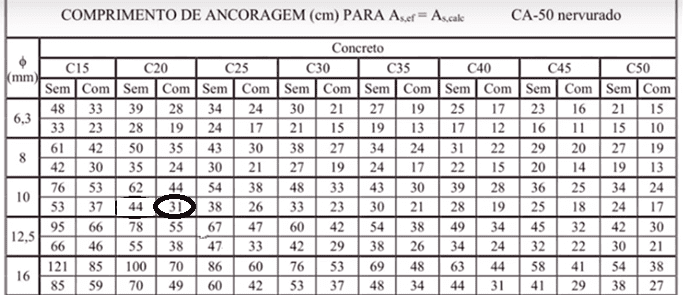
Altura útil da sapata (d) = h – cobrimento = 50 – 5 = 45cm
Altura da saia da fundação (h0’) > 15 ou h / 3
h / 3 = 15, então h0 = 15cm
Cálculo dos balanços (ca) = (a – ap) / 2 = (75 – 25) / 2 = 25cm
cb = (b – bp) / 2 = (65 – 15) / 2 = 25cm
α = atan ((h – h0) / ca) = atan (50 – 15) / 25 = 54,46º
h/2 = 25 cm
ca = 25 cm
2 * h = 100 cm
h/2 ≤ ca ≤ 2*h; 25 ≤ 25 ≤ 100; ok!
Cálculo dos momentos
σmáx = ((1,4 * Nk) / (a * b)) * (1 + (6 * e / a)) = ((1,4 * 92,2) / (75 * 65)) * (1 + (6 * 1 / 75)) = 0,028kN/cm²
σmín = ((1,4 * Nk) / (a * b)) * (1 – (6 * e / a)) = ((1,4 * 92,2) / (75 * 65)) * (1 – (6 * 1 / 75)) = 0,024kN/cm²
Cálculo das distâncias xa e xb
xa = ca + 0,15 * ap = 25 + 0,15 * 25 = 28,75 cm
xb = cb + 0,15 * bp = 25 + 0,15 * 15 = 27,25 cm
Tensões no solo na seção de referência S1A
P1.a = σmáx – ((σmáx – σmín) / a) * xa = 0,028 – ((0,028 – 0,024) / 75) * 28,75 = 0,026 kN/cm²
Reação de apoio (P1) = p1.a * xa = 0,026 * 28,75 = 0,747 kN
Reação de apoio (P2) = (σmáx – P1.a) * xa / 2 = (0,028 – 0,026) * 28,75 / 2 = 0,029 kN
M1a = ((P1 * xa / 2) + (P2 * (xa * 2 / 3))) * b = ((0,747 * 28,75 / 2) + (0,029 * (28,75 * 2 / 3))) * 65 = 734,110 kN.m
Pméd = (σmáx + σmín) / 2 = (0,028 + 0,024) / 2 = 0,026
M1b = pméd * (xb² / 2) * a = 0,026 * (27,25² / 2) * 75 = 723,998 kN.m
Cálculo das áreas de aço
As.a = M1a / (0,85 * d * fyd) = 734,110 / (0,85 * 45 * 43,478) = 0,441 cm²
As.a.mín = 0,0015 * bw * h = 0,0015 * 75 * 15 = 1,6875 cm²; Adota-se As.a.mín.
As.b = M1b / (0,85 * d * fyd) = 723,998 / (0,85 * 45 * 43,478) = 0,435 cm²
As.b.mín = 0,0015 * bw * h = 0,0015 * 65 * 15 = 1,462 cm²; Adota-se As.b.mín.
Considera-se 3 barras no sentido a. De acordo com a tabela de aço da figura temos barras com diâmetro de 10 mm.
Espaçamento (s) = 85 / n = 85 / 3 = 28,33, arredonda-se para 28.
Considera-se 3 barras no sentido b. De acordo com a tabela de aço da figura temos barras com diâmetro de 10 mm.
Espaçamento (s) = 75 / n = 75 / 3 = 25.
Figura 27. Projeto estrutural da Sapata.
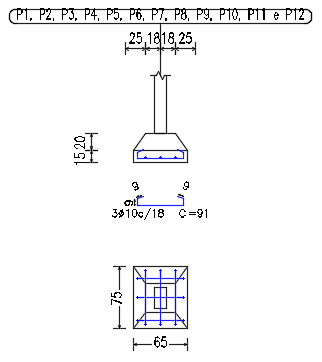
16. COMPARAÇÃO DE RESULTADOS
O pilar dimensionado foi o P8 e abaixo temos uma tabela comparando as medidas e armaduras encontradas:
| Pilar P8 | Dimensionamento automático pelo software | Verificado por cálculos tradicionais de dimensionamento |
| Medida em X | 15 | 15 |
| Medida em y | 25 | 25 |
| Armadura longitudinal | 4 Ø 12.5 | 4 Ø 10.0 |
| Diâmetro do estribo | 6.3 mm | 5 mm |
| Espaçamento do estribo | 15 cm | 12 cm |
O pilar P8 verificado por cálculos tradicionais apresenta armaduras e estribos com diâmetros menores. O espaçamento é menor, mas percebe-se que o cálculo manual trouxe um dimensionamento mais econômico.
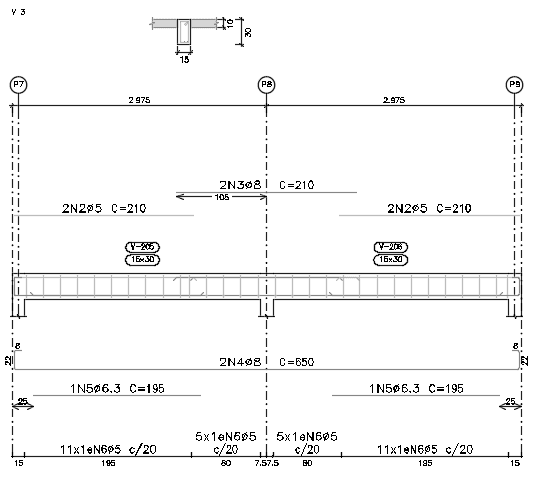
A viga dimensionada foi a V3 e a tabela de comparação está abaixo:
| Viga V3 | Dimensionamento automático pelo software | Verificado por cálculos tradicionais de dimensionamento |
| Altura da viga | 30 cm | 30 cm |
| Largura da viga | 15 cm | 15 cm |
| Armadura superior no trecho 1 e 3 | 2 Ø5 mm | 2 Ø5 mm |
| Armadura superior no trecho 2 | 2 Ø6.3 mm e 1 Ø8 mm |
2 Ø8 mm |
| Armadura inferior no trecho 1 e 3 | 1 Ø6.3 mm | 1 Ø6.3 mm |
| Armadura inferior ao longo da viga | 2 Ø6.3 mm | 2 Ø8 mm |
| Diâmetro do estribo | 5 mm | 5 mm |
| Espaçamento do estribo | 16 ou 15 cm | 20 cm |
A armadura superior no trecho 2 tem quantidade menor de aço de acordo com o cálculo manual, mas a armadura inferior ao longo da viga foi mais econômica quando dimensionada pelo software. O cálculo convencional ainda permitiu um espaçamento maior e no geral uma menor quantidade de armaduras. Abaixo temos a figura da viga e os 3 trechos para visualização.
Figura 28. Projeto estrutural da viga 203.
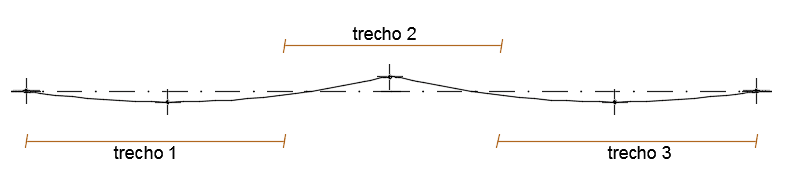
A laje dimensionada foi a laje 3 e a tabela de comparação de armaduras está abaixo:
| Laje 3 | Dimensionamento automático pelo software | Verificado por cálculos tradicionais de dimensionamento |
| Altura da laje | 10 cm | 10 cm |
| Armadura transversal inferior e espaçamento | 24 Ø5 mm Espaçamento = 13 cm | 24 Ø5 mm Espaçamento = 13 cm |
| Armadura longitudinal inferior e espaçamento | 22 Ø5 mm Espaçamento = 13 cm |
22 Ø5 mm Espaçamento = 13 cm |
| Armadura transversal superior e espaçamento | 24 Ø4.2 mm Espaçamento = 13 cm | 15 Ø5 mm Espaçamento = 20 cm |
| Armadura longitudinal superior e espaçamento | 14 Ø5 mm Espaçamento = 20 cm | 14 Ø5 mm
Espaçamento = 20 cm |
Na laje tivemos os resultados mais parecidos calculados pelo software e manualmente. A diferença está na armadura transversal superior. O software dimensionou armaduras com espessura menor, mas houve a necessidade de um espaçamento menor. Pode-se considerar dimensionamentos equivalentes entre as 2 opções.
A sapata dimensionada foi a S8 e abaixo está a comparação do dimensionamento.
| Sapata S8 | Dimensionamento automático pelo software | Verificado por cálculos tradicionais de dimensionamento |
| Medida em X | 85 cm | 65 cm |
| Medida em y | 85 cm | 75 cm |
| Altura da sapata | 30 cm | 35 cm |
| Armadura longitudinal | 3 Ø10 mm | 3 Ø10 mm |
| Comprimento da barra | 118 cm | 91cm ou 101cm |
O cálculo manual trouxe resultados melhores para as sapatas. As medidas em x e y menores permitiram também uma menor quantidade de aço na armadura.
17. CONSIDERAÇÕES FINAIS
Sabe-se que os softwares de cálculo aumentaram a velocidade de execução de projetos estruturais e apresentam um satisfatório grau de confiabilidade nos dimensionamentos. Mas ainda devem ser utilizados como ferramenta de auxílio. O projetista pode ter estruturas superdimensionadas se deixar a análise somente para os softwares.
Os resultados desse trabalho mostraram que é possível economizar na estrutura se forem feitas análises manuais profundas nas estruturas. Esse projeto é de pequeno porte e melhorias foram possíveis. Em projetos de grande porte o estudo do engenheiro civil pode trazer maiores economias em comparação com dimensionamentos automatizados. Deve-se lembrar também que é possível alterar dimensionamentos feitos pelos softwares. Um projetista pode alterar armaduras e medidas de peças estruturais nos softwares manualmente, mas para isso deve ter conhecimento profundo de normas e cálculos para verificações.
18. REFERÊNCIAS
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – procedimentos. Rio de Janeiro, 2014.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. Projeto e execução de fundações – Procedimento: NBR 6122. Rio de Janeiro, 1996.
BASTOS, Paulo Sérgio dos Santos. Fundamentos do Concreto Armado. 2006. 98 f. Estruturas de Concreto I, Curso de Engenharia Civil da Faculdade de Engenharia, da Universidade Estadual Paulista – UNESP, Campus de Bauru, 2006.
CARVALHO, Roberto Chust; FIGUEIREDO FILHO, Jasson Rodrigues de. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado. 3. ed. São Carlos: Edufscar, 2009.
DUCATTI, V. A. Concreto de elevado desempenho: estudo da aderência com a armadura. 1993. 259f. Tese (Doutorado em Engenharia) – Escola Politécnica, Universidade de São Paulo, São Paulo.1993.
GIONGO, José Samuel. Concreto armado: Projeto estrutural de edifícios. Apostila – Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, SP, 2007.
PINHEIRO, Libânio Miranda; Fundamentos do Concreto e Projeto de Edifícios. São Carlos: Edufscar, 2004.
ROCHA, A. M., Concreto Armado, Volume 1, Editora Nobel, São PauloRio de Janeiro,1981.
RODRIGUES, Paulo Cesar. Notas de Aula da disciplina de Estruturas deConcretoArmado I. Curso de graduação em Engenharia Civil. Universidade Regional do Noroeste do Estado do Rio Grande do Sul. Ijuí, 201.
SILVA, Ney Amorim. Concreto Armado I – (Apostila utilizada em sala de aula) Escola de Engenharia da UFMG, Departamento de Engenharia de Estruturas DEEs, Belo Horizonte 2005.
VALLE, Ângela do; ROVERE, Henriette Lebre La; Pillar, Nora Maria De Patta. Apostila de análise estrutural I. Apostila – Universidade Federal de Santa Catarina, Florianópolis, SC, 2013.
[1] Engenheiro civil; Especialista em Projeto, execução e dimensionamento de Estruturas e Fundações; Especialista em Gestão de Projetos em Engenharias e Arquitetura.
Enviado: Setembro, 2019.
Aprovado: Outubro, 2019.
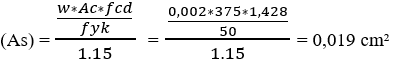
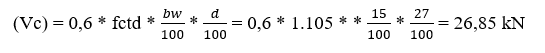
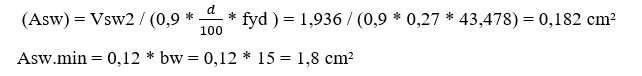


Uma resposta
Muito bom o material