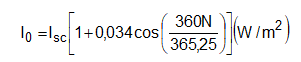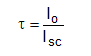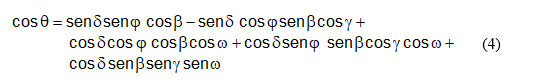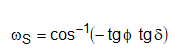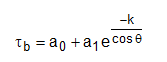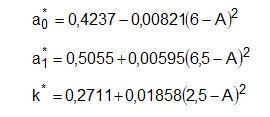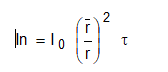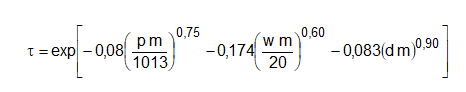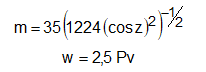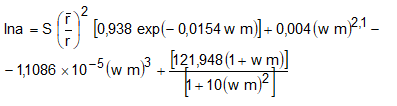ARTIGO ORIGINAL
PAIVA, Edinei Canuto [1]
PAIVA, Edinei Canuto. Energia Solar, no topo da atmosfera, ao nível do solo e simulações. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 12, Vol. 07, pp. 51-68 Dezembro de 2018. ISSN:2448-0959. Link de Acesso: https://www.nucleodoconhecimento.com.br/engenharia-agricola/no-topo-da-atmosfera
RESUMO
Este trabalho foi realizado com o objetivo de se fazer um estudo sobre a constante solar, a partir das relações astronômicas terra-sol e chegar a um modelo teórico para a intensidade da radiação no nível do solo. Após o estudo da radiação solar e sua interação com a atmosfera foi possível chegar a um modelo que estime a radiação solar ao nível do solo. Por fim foram feitas simulações para quantificar a quantidade de energia solar disponível em cada metro quadrado de superfície para diferentes latitudes. As simulações foram feitas para plana horizontal, superfície inclinada e superfície móvel. Os resultados indicam que as superfícies móveis apresentam um ganho de energia consideravelmente maior do que as superfícies fixas, sendo elas inclinadas ou não.
Palavras chave: Constante solar, Espalhamento, Irradiância.
INTRODUÇÃO
O sol é uma fonte singular de energia renovável situada no centro do sistema solar emitindo energia na forma de ondas eletromagnéticas numa taxa extremamente grande e relativamente constante. A taxa de emissão é equivalente à emitida por um forno de 6050K. Se fosse possível coletar a energia proveniente de 25 hectares da superfície do sol, ter-se-ia energia suficiente para suprir a demanda mundial.
Entretanto isto é impossível, veja três razões. Primeiro a terra se encontra a uma distância muito grande do sol, assim recebe apenas uma fração da energia emitida pela superfície do sol. Segundo a terra gira e recebe energia apenas uma parte do dia. Terceiro os efeitos da atmosfera terrestre diminui a intensidade da radiação na superfície terrestre, que na melhor das hipóteses causa uma perda de 30%, podendo variar com as condições atmosféricas como no caso de incidência de nuvens que pode ficar dias cobrindo o sol.
A taxa com que a energia solar chega à superfície terrestre é chamada de irradiância solar ou insolação e tem como unidade de medida no, sistema internacional de unidades (SI), é o Watt por metro quadrado (W / m ²). A irradiância é uma grandeza instantânea que varia no tempo. O valor Máximo da irradiância determina o pico de energia que entra no sistema, e deve ser usada para a construção do projeto. Se o armazenamento de energia for incluído ao sistema, o projetista deve conhecer também a variação da irradiância no tempo para aperfeiçoar o design do sistema.
Para um projetista de sistemas de coletores solares é também interessante saber quanto de energia chega ao coletor num período de um dia, uma semana, ou ano. Este somatório é chamado de radiação ou irradiação. A unidade de medida para radiação solar é joules por metro quadrado (J / m²), mas também pode ser usado watt-hora por metro quadrado ( W h/m²).
Como é mostrada, a seguir, a radiação solar é simplesmente a integração ou o somatório da irradiância solar num dado intervalo de tempo.
1.1 A CONSTANTE SOLAR
A intensidade de radiação na superfície do sol é aproximadamente 6,33 x 10 7 W / m². Como a intensidade cai com o quadrado da distância, na terra esta é de apenas , como ilustra a Figura 1.
Figura 1: Divergente de energia a partir do sol até a terra.
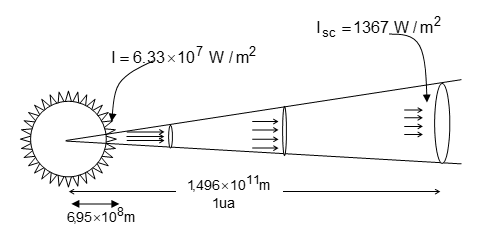
A intensidade de radiação proveniente do sol é relativamente constante. Portanto, a radiação solar, a uma distância de uma unidade astronômica (ua) é chamada de constante solar, lsc , e tem seu valor aceito como 1367 W/m 2 (IQBAL, 1983).
Outros valores para a constante solar são históricos na literatura como, 1,353 W/m 2 aparece em muitas publicações. Estes geralmente trazem discrepâncias devido a erros de calibração de instrumentos de medição (WHITE, 1977). A constante solar pode sofrer variações que não ultrapassam 0,25% para ciclo de 11 anos e para manchas solares nunca são superiores a 1%.
Apesar de a constante solar apresentar variações que são estudadas por terem potencial impacto sobre o clima, ela não é de primeira importância nos coletores solares. É estimado que uma diminuição apenas de 1% possa reduzir em 1ºC a temperatura média do planeta e que a terra seria coberta de gelo se a radiação decrescesse de 6%.
O tamanho angular aparente do disco solar pode ser calculado a partir do diâmetro da fotosfera e da distância terra-sol que a 1ua este é de 0,553 graus. A distância terra-sol varia de mais ou menos 1,7% devido a sua órbita elíptica.
1.2 ESPECTRO SOLAR EXTRA TERRESTRE
O espectro da radiação solar no topo da atmosfera se compara a uma curva de radiação espectral de um corpo negro a 6050K. Onde 45% da energia irradiada está compreendida em comprimentos de onda na faixa do espectro visível, normalmente entre 0,3 e 0,7 micrometros. Apenas uma pequena parte, por volta de 1% encontra-se na faixa de ondas curtas (UV e raios-x) os outros 54 % se encontra na região do infravermelho. O espectro solar varia ligeiramente quando atravessa a atmosfera terrestre.
Saber como a energia solar está distribuída nos vários comprimentos de onda permite ao engenheiro avaliar o impacto de fenômenos ondulatórios sobre a energia total coletada.
Para fazer considerações a respeito dos parâmetros dependentes do comprimento de onda (transmitância do vidro, obsorbância de uma superfície, ou resposta de foto células) é sempre proveitoso plotar esse parâmetro versus uma escala representando a porcentagem de energia solar contida naquele comprimento de onda. A área sobre a curva representa a porcentagem total de energia de todos os comprimentos de onda. E também uma escala não linear representando os comprimentos de onda pode ser incluída. Assim a dependência desde parâmetro com o comprimento de onda fica visualmente mostrada.
1.3 IRRADIÂNCIA SOLAR EXTRATERRESTRE
A constante solar é um parâmetro usado para caracterizar a entrada de radiação solar no topo da atmosfera sendo variável ao longo do ano devido a efeitos astronômicos como órbita da terra em torno do sol, manchas solares e ainda é função do comprimento de onda emitido, estudados em um novo enfoque da ciência, climatologia espacial (MARTINS, 2004).
Devida a órbita ligeiramente elíptica a intensidade da radiação solar recebida fora da atmosfera terrestre varia mais ou menos 3,4% com irradiância máxima ocorrendo no periélio (3-5 de janeiro) e o mínimo no afélio ( 5 de julho). Esta variação pode ser estimada na equação 1.
Onde I0 é a irradiância solar fora da atmosfera terrestre e N é o acréscimo dia do ano (começando em 1º de janeiro).
Um conceito sempre usado nos modelos de irradiância solar é que a irradiância solar extraterrestre é aquela incidente sobre uma superfície horizontal. Considerando uma superfície plana fora da atmosfera terrestre paralela ao solo. Onde a face desta superfície (normal ao raio central) fica voltada para o sol e recebe I0° Máximo possível de radiação solar.
Se a superfície não é normal aos raios solares, a irradiância sobre ela será reduzida com o cosseno do ângulo entre o vetor normal e o vetor que aponta diretamente para o centro do sol. Este conceito é ilustrado na Figura 2, onde se pode ver que a taxa em que a energia incidente em ambas as superfícies é a mesma. Entretanto a área da superfície é grande em relação à sua projeção, superfície hipotética B, fazendo com que a quantidade de energia incidente por unidade de área em A seja menor que em B.
Figura 2: O efeito cosseno e a irradiância extraterrestre. Adaptada de (ALVES, 2008)
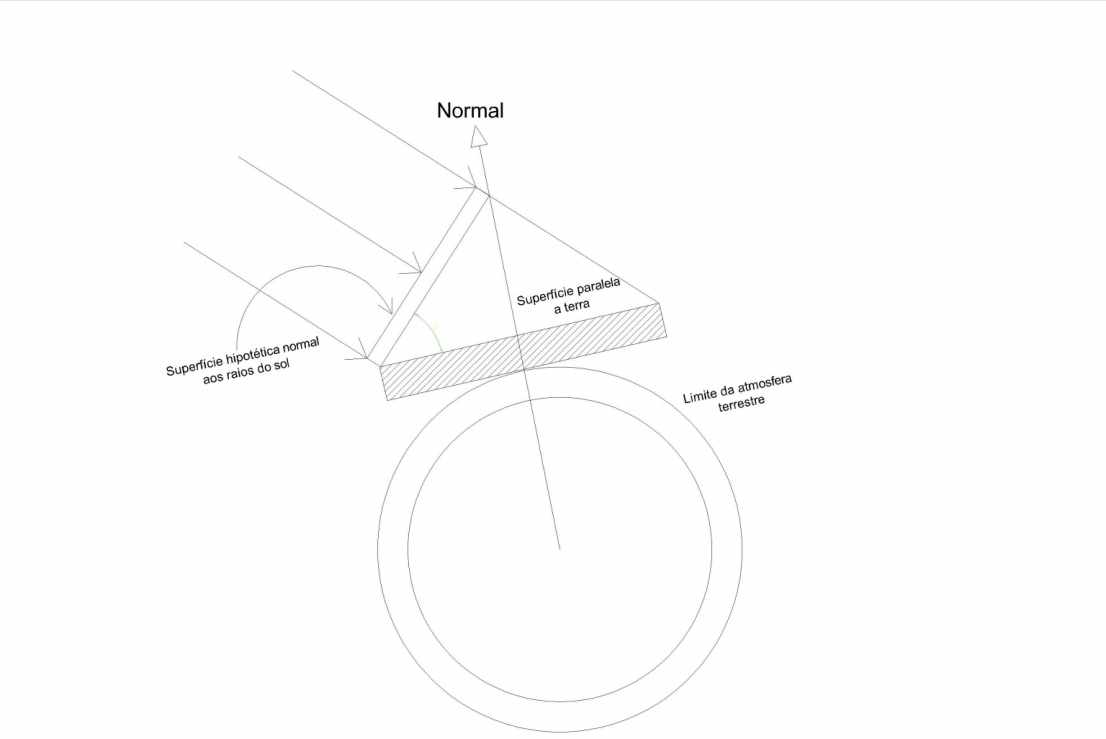
A irradiância solar extraterrestre sobre uma superfície paralela ao solo é I0,h = I0 cos0z onde I0 é a irradiância solar extraterrestre e 0z o ângulo entre as duas superfícies, que é o mesmo ângulo que os raios solares fazem com a normal à superfície terrestre, conhecido como ângulo zenital. A relação entre a radiação da radiação pelo cosseno do ângulo zenital é chamado de efeito cosseno. O efeito cosseno é um conceito extremamente importante na otimização da orientação de coletores solares.
Devido ao efeito cosseno, a irradiância solar extraterrestre sobre uma superfície horizontal varia ciclicamente com a rotação da terra em torno de seus eixos.
A irradiância solar que incide na superfície da terra dependerá destes efeitos, além de outros associados à interação da radiação eletromagnética com os constituintes da atmosfera da terra. A transmissão da radiação solar na atmosfera é um processo complexo e de difícil descrição devido ao grande número de propriedades físicas da atmosfera que a influenciam.
A razão entre a irradiância solar na superfície terrestre e no topo da atmosfera é definida como transmitância atmosférica (Equação 2).
Ao atravessar a atmosfera, a radiação eletromagnética é atenuada por processos de espalhamento e absorção causados pelas partículas (denominados aerossóis) e moléculas de gases atmosféricos. Assim quando chega à superfície a radiação solar global Rg , apresenta duas componentes, difusa Rc (espalhada pela atmosfera) e direta Rd (equação 3).
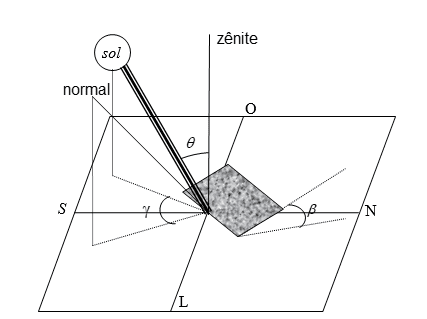
As relações geométricas entre um plano em uma orientação particular num dado instante e a radiação direta incidente (que é a posição relativa do sol em relação ao plano) foram descritas em termos de uma série de ângulos (DUFFIE & BEKMAN, 1980). Figura 3.
A equação 4 relaciona o ângulo de incidência e os outros ângulos.
em que
φ → Latitude, que é a localização angular ao norte ou ao sul do equador, assumindo valores positivos para o norte – 90 ≤ φ ≤ 90° ;
δ → Declinação solar, é a posição angular do sol em relação ao equador sendo positivo para o hemisfério norte e negativo para hemisfério sul -23,45° ≤ δ ≤ 23,45°;
β → Inclinação, ou seja, o ângulo entre a superfície considerada e a horizontal no local 0° ≤ β ≤ 180° ( β>90° o plano está coma a face voltada para baixo);
γ → Azimute da superfície é o ângulo formado entre a projeção do sol e da normal à superfície no plano horizonte local;
ϖ → Ângulo horário, desvio do sol a oeste ou a leste do meridiano local devido a rotação da terra. Negativo pela manhã e positivo a tarde.
∅ → Ângulo de incidência e o ângulo entre o feixe de radiação e a normal ao horizonte local (zênite).
Figura 3: Azimute, ângulo de incidência e ângulo de inclinação do plano.
A declinação solar, δ , pode ser estimada por meio da equação 5, de COOPER (1969).
em que n é o enésimo dia do ano, conhecido como dia juliano.
Ao penetrar na atmosfera a radiação solar atravessa uma massa de ar (caminho óptico). A espessura da camada de ar varia com o ângulo de incidência da radiação (ângulo θ ) da seguinte forma (Equação 6):
m=(cosθ)-1
Esta relação é valida para 0 < θ < 70°, para ângulo de incidência maior que setenta graus a relação acima começa a apresentar desvio significativo (ROBINSON, 1966 E KONDRATYEV, 1969).
O somatório da radiação solar recebida sobre uma superfície horizontal no topo da atmosfera forma um limite superior para energia total que incide sobre uma superfície horizontal abaixo da atmosfera, mas sem a complicação da massa de ar e cobertura por nuvens.
A energia total depositada sobre uma superfície num dado período de tempo é encontrada por integração (ou somatório) da irradiância solar neste intervalo de tempo. Esta soma é chamada de radiação solar e tem unidade de energia por unidade de área.
È sempre interessante determinar a energia total que incide sobre uma superfície ao longo do dia. A radiação solar extraterrestre sobre uma superfície horizontal dado por pode ser calculada a partir de valores instantâneos da irradiância solar extraterrestre.
Onde o tempo é medido em segundos e varia do sol nascente (ns) até o pôr do sol (ps). Usando as relações geométricas terra-sol foi possível desenvolver uma expressão abaixo para a radiação solar extraterrestre sobre uma superfície paralela à terra.
Onde, ϖs, é o ângulo horário do por do sol dado em função da declinação solar e latitude (equação 9).
Todos estes ângulos e tem unidade de radianos nesta equação. Desde que a constante 86400 tenha unidade de segundos a unidade da irradiância solar extraterrestre deve ser Watt por metro quadrado (W/m ²).
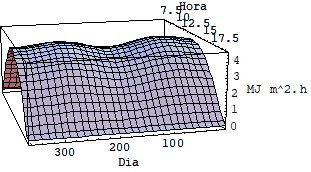
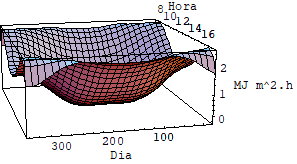
Valores da radiação solar extraterrestre sobre uma superfície horizontal para um período de um ano, para três latitudes, usando a equação 3 são mostrados na Figura 4.4. Esta figura mostra pontos interessantes sobre a energia que recebemos do sol. Note que o maior valor de energia incidente diária ocorre em latitude norte no verão. Também pode perceber que no equador a radiação mais alta ocorre na primavera e no outono (nos equinócios) e não no verão como poderia se esperar. O valor máximo ocorre no verão apenas para latitudes acima de 23,5 graus.
A energia total acumulada em um ano é a integral da radiação solar mostrada na Figura 4. Como pode se esperar, o somatório da radiação solar sobre uma superfície horizontal é maior no equador. Superfícies em grandes latitudes perdem muita energia com o efeito cosseno, discutido anteriormente.
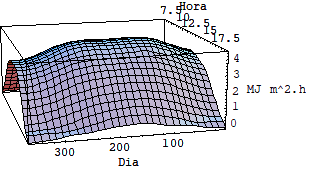
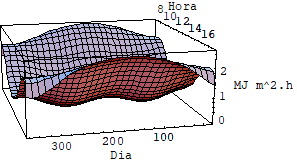
Se a superfície é colocada voltada para o sol (mas considerando-a fora da atmosfera) a radiação solar extraterrestre varia como mostra a Figura 5. Quando a latitude aumenta em direção ao norte, maior será a energia disponível no verão e menor no inverno.
Figura 4: Variação sazonal da radiação solar extraterrestre diária incidente sobre uma superfície horizontal fora da atmosfera terrestre.
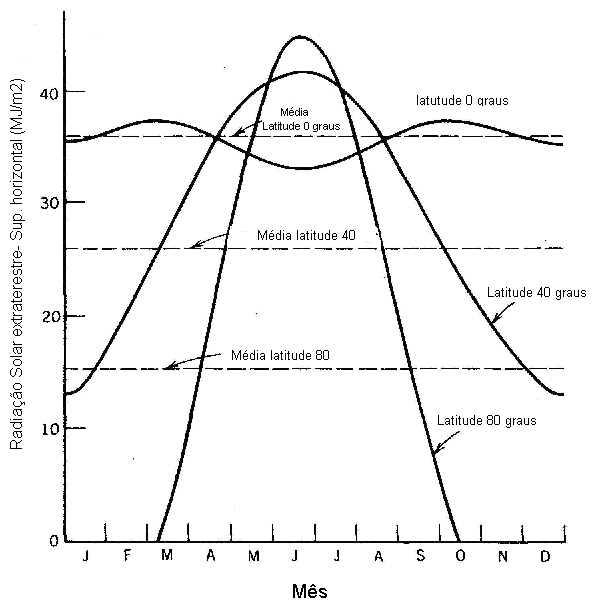
Figura 5: Variação sazonal da radiação solar extraterrestre diária incidente sobre uma superfície colocada normal aos raios solares, fora da atmosfera terrestre.
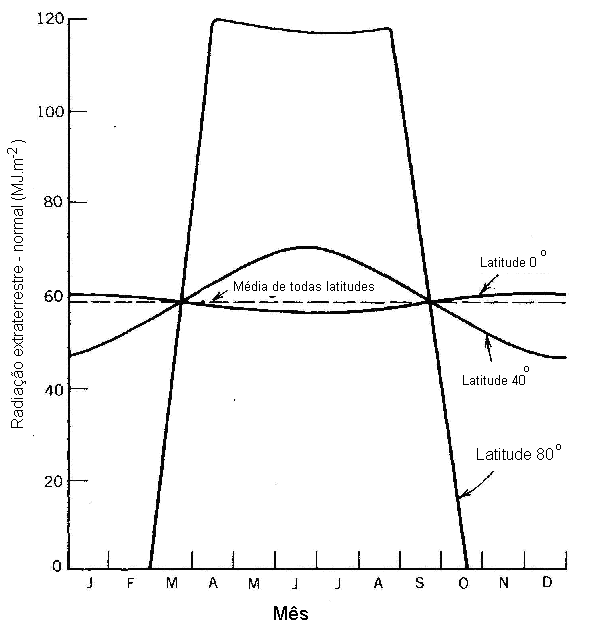
Ainda percebe-se que a radiação solar anual sobre uma superfície mantida perpendicular aos raios solares é essencialmente a mesma para todas as latitudes. Isso acontece porque em qualquer lugar a terra recebe 4380 horas de radiação. Entretanto existe uma diferença na radiação solar durante o inverno, aumentando 6% para o verão, mas a média anual se mantém constante.
Nota-se também que a média anual corresponde ao valor de radiação de um dia com duração de 12 horas. O que corresponde a 59,1MJ/ m ² . Comparando a Figura 4 com a Figura 5 percebe-se que o efeito cosseno reduz a radiação solar sobre a superfície horizontal em 39% no equador, 52% para uma latitude de 40 graus e até 74% para uma latitude de 80 graus.
É importante estudar a radiação solar sobre uma superfície hipotética acima da atmosfera terrestre porque dá uma idéia dos efeitos da mecânica do sistema terra-sol sobre a energia recebida. A seguir são mostrados os efeitos da atmosfera terrestre (vapor d’agua, dióxido de carbono, nuvens, neblina e particulados) sobre a radiação solar abaixo da atmosfera.
2. CARACTERÍSTICAS DA RADIAÇÃO SOLAR AO NÍVEL DO SOLO
A medida que a radiação atravessa a atmosfera, esta é absorvida, refletida, espalhada e transferida diretamente.
Na superfície da terra o sol tem baixa intensidade, uma cor diferente e uma forma diferente do abservado acima da atmosfera.
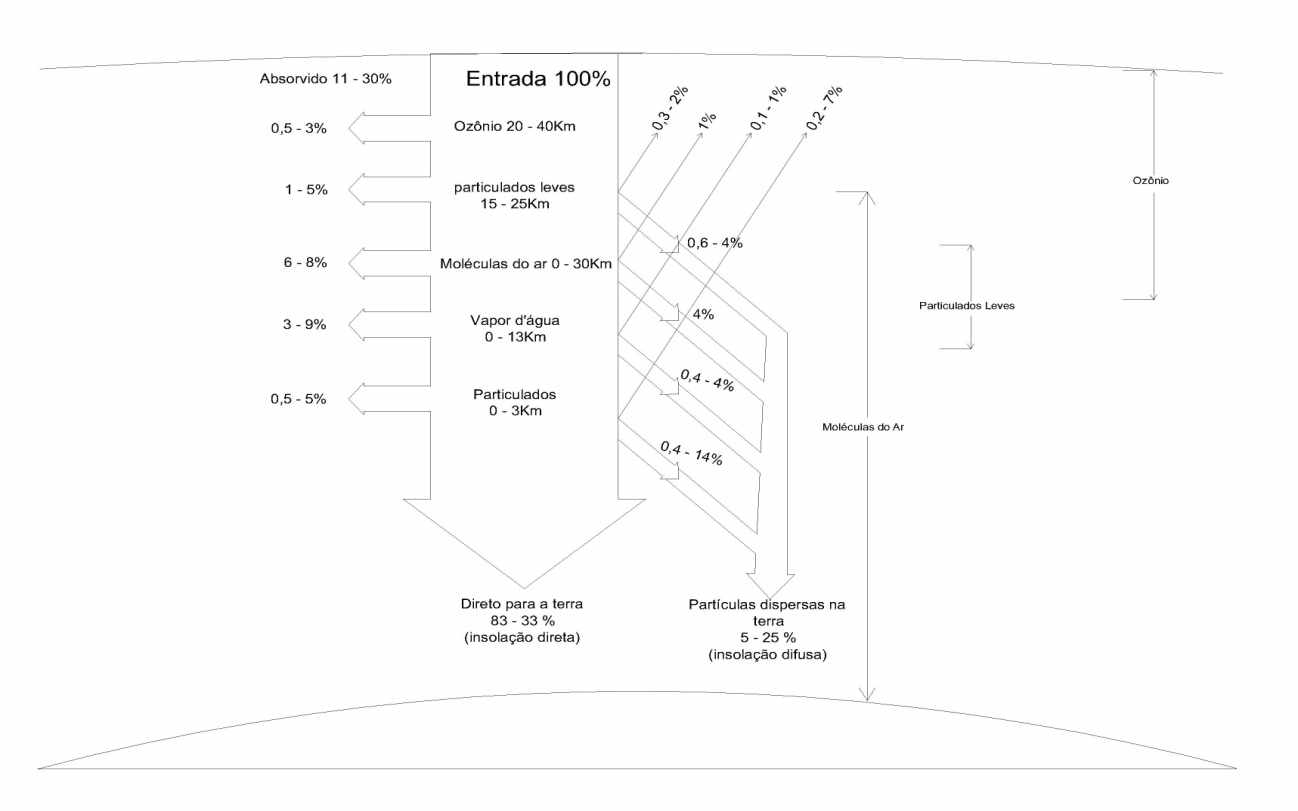
A atmosfera causa uma redução na irradiação solar em torno de 30% em um dia claro e aproximadamente 90% em dias muito nublados.
A Figura 6 ilustra a quantidade de energia absorvida e espalhada (refletida e difundida) causada por diferentes componentes atmosféricos.
Figura 6: Absorção e espalhamento da energia solar incidente na atmosfera. Valores típicos para uma massa de ar.
2.1 RADIAÇÃO DIRETA SOBRE UMA SUPERFÍCIE EM MOVIMENTO
Até aqui foi apresentada uma metodologia para estimar a radiação solar sobre superfícies fixas, como janelas, coletores planos ou superfícies inclinadas. O mais importante para o presente trabalho é estimar a intensidade da radiação sobre superfícies que seguem caminhos predeterminados.
Os coletores concentradores utilizam mais efetivamente a radiação direta, portanto é necessário que mantenham suas faces voltadas para o sol e para isso é interessante que se tenha pelo menos dois eixos de rotação, um para corrigir a declinação solar e outro para corrigir o ângulo horário.
A radiação solar direta sobre uma superfície em qualquer instante pode ser estimada por meio da equação 10.
em que é calculado pela equação (4).
O principal problema da equação (10) é a determinação da transmitância atmosférica para a radiação, τΒ . Hottel, em 1976, apresentou um método para estimar a transmitância atmosférica (equação 11).
em que , e são constantes para uma atmosfera típica, com 23 km de visibilidade e podem ter seus valores estimados a0*, a1* e k* , para altitudes inferiores a 2,5 km, pelas relações 12, 13 e 14.
em que é altitude do local observado em quilômetros.
Para viçosa-MG tem A é igual 0,65 km o que resulta nos coeficientes de Hotel a seguir:
a*0= 0,189
a1*= 0,709
k*= 0,335
3. RADIAÇÃO GLOBAL SOBRE SUPERFÍCIES E SIMULAÇÕES
Como já foi dito a radiação solar ao atravessar a atmosfera sofre atenuações, dessa forma, a radiação global chega á superfície dividida em componentes, direta (In) e difusa (Di).
A radiação global pode estimada pela equação 15.
em que é ângulo de incidência da radiação direta, no caso de superfície horizontal é o próprio ângulo zenital do sol.
De acordo com Brooks, a irradiância solar direta pode ser estimada por meio da equação 16.
Sendo a constante solar, a distância terra-sol, a distância media terra-sol e a transmitância atmosférica, dada por:
em que:
p = pressão atmosférica em (mb);
m = massa ótica de ar (adimencional);
w = quantidade de água preciptavel na atmosfera (mm);
d = parâmetro adicional de poeiras.
A quantidade de água precipitável é dada pela fórmula de Hann (equação 1.) e, massa ótica de ar varia com o ângulo zenital do sol (z) e pode ser estimada pela equação 18:
sendo a pressão de vapor d’água em milibars. Para Viçosa-MG, o valor encontrado de w foi 0,41,para junho.
A radiação difusa é dada por:
sendo K um coeficiente empírico, que para o Congo, por exemplo, obteve-se:
A irradiância solar direta sobre uma superfície normal aos raios ao nível do solo, considerando apenas o vapor d`agua como agente atenuador pode ser estimada por:
em que w é expresso em milímetros.
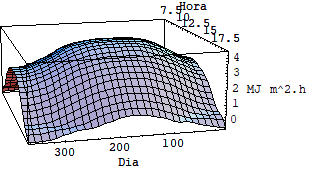
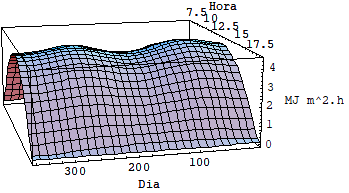
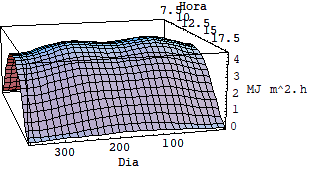
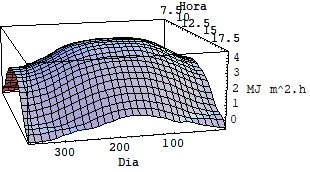
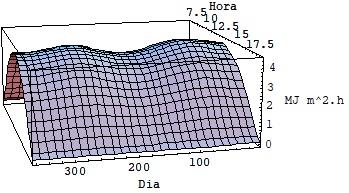
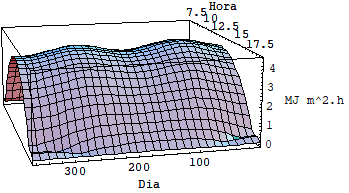
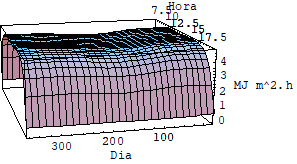
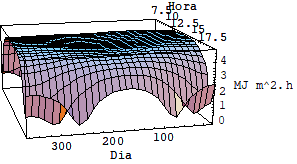
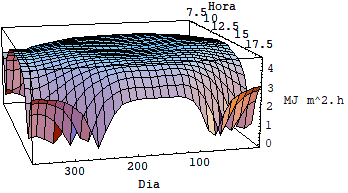
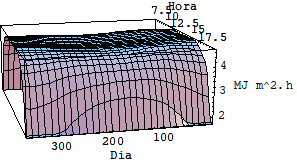
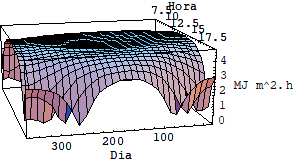
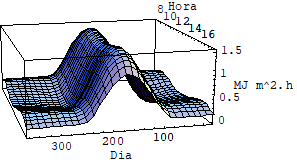
Usando as equações acima foi possível fazer uma simulação utilizando se o software mathematica e avaliar as diferenças entre a intensidade de radiação incidente sobre superfícies horizontais fixas, inclinadas fixas e moveis sob dois graus de liberdade. Veja o quadro de gráficos a seguir.
3.1 RESULTADO DAS SIMULAÇÕES
Rg s Rg superfície horizontal fixa latitude 0º
Rg superfície horizontal fixa latitude 20º
Rg superfície horizontal fixa latitude 40º
Fg superfície fixa com i = latitude 10º
Rg superfície horizontal fixa latitude 10º
Rg superfície horizontal fixa latitude 30º
Fg superfície fixa com i = latitude 0º
Fg superfície fixa com i = latitude 20º
Rg superfície fixa com i = latitude 40º
Rg superfície com 2 graus de liberdade i=z e azimute=a latitude 10º
Rg superfície com 2 graus de liberdade i=z e azimute=a latitude 30º
Rg superfície fixa com i = latitude 30º
Rg superfície com 2 graus de liberdade i=z e azimute=a latitude 0º
Rg superfície com 2 graus de liberdade i=z e azimute=a latitude 20º
Rg superfície com 2 graus de liberdade i=z e azimute=a latitude 40º
Diferença entre Rg sup horiz fixa e 2GL Lat = 10º
Diferença entre Rg sup horiz fixa e 2GL Lat = 20º
Diferença entre Rg sup horiz fixa e 2GL Lat = 40º
Diferença entre Rg sup fixa inclinada de Lat e 2GL lat=10º
Diferença entre Rg sup fixa inclinada de Lat e 2GL Lat = 20º
Pela analise dos cinco últimos gráficos fica clara a diferença entre o nível de radiação em superfícies fixas e superfícies móveis que rasteiam o sol.
É evidente que no modelo simulado não se levou em conta o aparecimento de nuvens e também, pressão atmosférica, água precipitável e parâmetro de poeiras foram considerados constantes. Embora todos estas grandezas são vaiáveis e participam da atenuação da radiação solar.
Outros fatores que podem influenciar na radiação recebida por uma superfície são possíveis erros e o consumo de energia do rastreador real.
DUFFIE e BECKMAN (1974), apresentam o efeito da orientação de uma superfície na radiação anual incidente para latitude de 35° norte, do sudoeste dos Estados Unidos (quadro abaixo).
| Orientação da superfície | Radiação | |
| 106 kJ/m2 | % | |
| 1. Horizontal fixa. | 5,34 | 100 |
| 2. Fixa, com inclinação igual a da latitude. | 6,19 | 115,9 |
| 3. Variável com ajuste contínuo no eixo norte-sul. | 7,43 | 139,1 |
| 4. Variável, com ajuste contínuo no eixo paralelo ao eixo da terra. | 8,14 | 152,4 |
| 5. Ajuste contínuo sobre os dois eixos para manter os raios solares perpendiculares à superfície. | 8,38 | 156,9 |
Conforme é mostrado no Quadro, a orientação da superfície influencia na radiação anual incidente (levando em consideração a nebulosidade). Nesse caso, a radiação solar incidente em superfície horizontal fixa foi de 5,34 x 106 kJ/m2 (100 %), em superfície com inclinação igual à latitude do local, 6,19 x106 kJ/m2 (115,9 %), já numa superfície com ajuste contínuo no eixo paralelo ao eixo da terra, a radiação incidente foi de 8,14 x 106 kJ/m2 (152,4 %).
4. CONSIDERAÇÕES FINAIS
Fazer um estudo da constante solar e desenvolver a capacidade de cálculo teórico da mesma é imprescindível para se ter previsões sobre a intensidade de radiação solar ao nível do solo. De posse destas previsões fica mais fácil dimensionar uma planta solar que atenda às exigências específicas de cada projeto.
As simulações realizadas apresentam a fração adicional de energia solar que poderá ser disponibilizada caso o sistema implantado possua um rastreador solar. Estes resultados podem ser usados como fator para tomada de decisão para aqueles que desejam implantar um sistema de energia solar com ou sem rastreador, uma vez que faz uma estimativa da quantidade extra de energia com o rastreador. Permitindo assim fazer uma planilha de custo benefício e escolher o sistema mais viável economicamente.
Outras variáveis podem ser adicionadas ao modelo para simulação, como por exemplo, a incidência de nuvens, porem a natureza estocástica dessa variável pode dificultar o entendimento dos resultados e até mesmos fornecer resultados com margem de erros mais elevadas.
REFERÊNCIAS
ALVES, A. F. Desenvolvimento de um Sistema de Posicionamento Automático para Painéis Fotovoltaicos. 2008. Tese (Doutorado em Agronomia) – Faculdade de Ciências Agronômicas, Universidade Estadual Paulista “Júlio de Mesquita Filho”, Botucatu-SP, 2008.
IQBAL MUHAMMED, An introduction to solar radiation, Academic Press, Canada, 1983.
THEKAEKARA M.P., Solar radiation meansuriment: Tecniques and instrumentation, Solar Energy, 18, 309 (1976).
MARTINS F.R., PEREIRA E.B. E ECHER M.P., Levantamento dos recursos de energia solar no Brasil com o emprego de satélite geoestacionário – o Projeto Swera, Revista Brasileira de Ensino de Física, v. 26, n. 2, p. 145 – 159, (2004).
COOPER P.I., The Absorption of Solar Radiation in Solar Stills, Solar Energy, 12, 3 (1969).
DUFFIE J.A. E BEKMAN W.A., Solar engineering of thermal processes,Wiley-Interscience, New York, 1980.
KONDRATYEV K.Y., Radiation in the atmosphere, Academic Press, Nova Iorque e Londres, 1969.
ROBINSON, N. (ed.), Solar Radiation, Elsevier, Amsterdam (1966).
HOTTEL H.C., A Simple Model for Estimating the Transmittance of Direct Solar Radiation Through Clear Atmospheres, Solar Energy, 18, 129 (1976).
Stine W. e Geyer M., Power from the Sun Solar, Energy Industries Association – SEIA, livro online disponível em: http://www.powerfromthesun.net/book.htm.
[1] Doutor em engenharia Agrícola. Mestre em física Aplicada. Graduado em física.
Enviado: Dezembro, 2018
Aprovado: Dezembro, 2018