ARTIGO ORIGINAL
AGUIAR, Samuel Ferreira de [1]
AGUIAR, Samuel Ferreira de. Imagem do campo escuro, unidade natural e efeito anamórfico. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed.02, Vol. 02, pp. 57-75. Fevereiro de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/fisica/campo-escuro, DOI: 10.32749/nucleodoconhecimento.com.br/fisica/campo-escuro
RESUMO
O presente artigo objetivou demonstrar, experimentalmente, a modelagem da unidade natural interativa utilizando o efeito anamórfico formado em tubo de alumínio, visando provar, por meio dela, a imagem microscópica do campo escuro e seu formato modelado naturalmente. Portanto, trata-se de uma pesquisa bibliográfica de cunho descritivo e qualitativo que possibilitou a identificação da imagem e do formato do campo escuro, visto a provação da sua densidade.
Palavras-chave: Campo escuro; efeito anamórfico; unidade natural.
1. INTRODUÇÃO
Este artigo tem por finalidade demonstrar, experimentalmente, a modelagem da unidade natural interativa utilizando o efeito anamórfico formado em tubo de alumínio e, por meio dela, comprovar a imagem microscópica do campo escuro e seu formato modelado naturalmente.
2. UNIDADE NATURAL E IMAGEM DO CAMPO ESCURO
Quando se trata da questão da interação entre sistemas de espaços mais sutis e matéria rígida, por vezes, a mesma aparece como sendo a maior dificuldade da Física moderna Snoke (2020), mesmo com muitos esforços acadêmicos válidos. Isso também se observa no conhecimento secular filosófico, com a necessidade de se estabelecer um formato modular entre esses estados mais sutis e as estruturas materiais consistentes. Existem fontes teóricas consideráveis e consistentes sobre o tema, mas fica evidente a dificuldade de uso para fins práticos, no sentido do desenvolvimento aplicacional. (KITTEL, 1996; MARTINS e MIHALY, 1996; HEINONEM e TAYLOR, 2002)
Neste sentido, a proposta deste artigo é encontrar algo mais sujeito à análise física que possa trazer, de forma visível, a demonstração dos estágios dessa interatividade, não representando apenas uma teoria, mas buscando a forma como os sistemas naturais realmente modelam e utilizam essa comunicação. Para isso, é utilizado o efeito anamórfico concebido em um simulador geométrico no formato de tubo, cujo efeito é explicado por Collins (1992).
Daqui para frente, o efeito anamórfico gerado em tubo de alumínio será utilizado para demonstrar que existe um estado de unidade natural, tornando possível, através deste, a identificação do modelo de imagem do campo escuro pela sombra projetada no tubo de alumínio, nos pontos da trilha similar interna.
O principal ponto aqui é mostrar que a sombra projetada a partir do efeito da luz no tubo de alumínio é a primeira forma básica que a natureza tem para diluir o campo escuro em um modelo de desenrolamento do campo, desacelerando o espaço e gerando este formato visível de unidade natural que interage com os anéis de cores, projetados no interior do tubo de alumínio, como mostrado na figura 3. Com este mesmo desenrolamento é possível mapear o modelo de imagem do campo escuro.
A eficiência comunicativa entre os sistemas naturais e seus níveis mais sutis, permite pensar que é quase certa a existência de uma unidade natural que interage por meio de uma característica similar a todos estes sistemas. Se isso ocorre é porque também, este ponto de combinação, que muito provavelmente poderá ser visto, apresenta a interação do campo escuro com essa região similar aos três sistemas: luz, espaço e geometria do tubo. Isso é o que será demonstrado nesse artigo, analisando, antes, os sistemas mais sutis conhecidos como espaço, luz e campo escuro.
A necessidade de um modelo a partir do qual todos os sistemas naturais se comunicam em um ponto comum, num formato interativo entre os três sistemas mais sutis, leva à observação do efeito dessa interação em tubo de alumínio. Foi pensando nessa unidade encontrada na análise subjetiva que esse artigo foi desenvolvido, projetando essas condições na experiência organizada através de um tubo de alumínio. O efeito satisfaz as necessidades e as previsões citadas anteriormente.
Para este estudo, feito nas áreas de ciências naturais, física e computação, as percepções filosóficas de Vacariu e Vacariu (2020) encontram respaldo na natureza. Assim, existe um ponto de auto simplificação na forma de unidade comunicativa e adaptativa denominada, neste artigo de unidade natural. Há um forte indicativo de que a natureza se utiliza dessa unidade para localizar, organizar, interagir e modelar sistemas, nos níveis mais sutis (REMORTEL, 2016).
Neste artigo são abordados três tipos de unidades sugeridas:
- Natural – Transparência da unidade.
- Interativa – Região da similaridade.
- Comunicativa – Linha de campo escuro.
2.1 BUSCA PARA ENCONTRAR A UNIDADE NATURAL, INTERATIVA E COMUNICATIVA
Em uma verificação teórica sobre pontos de interação entre múltiplos sistemas naturais, foi possível identificar essa ocorrência orquestrada a partir de pontos similares que surgem entre eles, onde se é possível a identificação desses pontos utilizando um simulador semelhante, com geometria cilíndrica ou modelo tubo.
As formas geométricas físicas e visíveis repetem-se nos níveis mais sutis em sistemas menos visíveis (PATY, 2010). Verifica-se, assim, uma ocorrência e necessidade natural de que as mesmas geometrias existam nos dois estados.
Analisando o raio de luz projetado em superfícies como alumínio cromado, é possível identificar uma característica homogênea e resplandecente. Essa característica é a mesma informação que caracteriza a unidade natural no tubo de alumínio. Porém, quando se projeta luz no modelo de tubo, o efeito se torna mais visível (figura 6), surgindo como uma densidade móvel adaptada à geometria do tubo utilizado. Aqui esse efeito será tratado como um adaptador sutil, um estado e um efeito que formam padrões espelhados no limite e orifício do simulador, a partir da luz refletida em tubo de alumínio.
A adaptação entre o movimento do efeito e a geometria cilíndrica ocorre através dos pontos similares identificados na linha de sombra ou espiral, que aparece no tubo de alumínio (figura 5).
Naturalmente, a integração geométrica entre o estado rígido do material que forma o tubo e seu efeito anamórfico ocorre na linha de sombra que é representada pela trilha similar e o ponto de diluição do campo que, por sua vez, atende aos princípios de orientação e movimento dessa unidade. Na mesma observação e experimento, é possível verificar a recorrência da forma de espiral ou sombra que forma no tubo de alumínio, e que pode ser tratada aqui como recorrência comunicativa. A unidade natural ou efeito anamórfico, gerado pela reflexão e motivação de limite do tubo e linha de sombra na forma de espiral, cria uma espécie de desenrolamento padrão e modelador natural gerado no comprimento interno do tubo até o limite final do orifício.
A partir desse ponto, é possível deduzir que este efeito gerado no tubo de alumínio interage e se move por indução da trilha principal – a mesma região que o campo escuro é desenrolado – na mesma perspectiva e trilha de sombra, sendo essa sombra responsável em modelar os anéis de forma a serem vistos dentro do tubo. Logo, essa ocorrência é a mesma que permite a visualização da densidade homogênea ou unidade natural junto à reflexão da luz. Neste caso, haveria dois tipos de diluição do campo escuro, através da frequência da luz e da orientação espacial, estabelecendo fortes indicativos de que a natureza utiliza as mesmas regiões interativas para os dois formatos.
A partir da apresentação seguinte, mostrando dados e elementos físicos, teóricos e experimentais, pode-se verificar que a natureza organizacional da matéria, espaço, luz e campo escuro, a partir de uma determinada combinação, localiza esse efeito de forma ao mostrar um condicionamento natural e uma modulagem entre os três sistemas visíveis mais sutis. Assim, as estruturas materiais mais rígidas passam a ter um canal para interagirem nestes níveis, uma vez que as três unidades (interativa, natural e comunicativa) tornam-se visíveis a partir de um ponto comum de interação, como demonstrado nas imagens a seguir. Esse formato de unidades naturais demonstra ser uma ferramenta eficiente para aplicação em muitos outros modelos e sistemas teóricos (ASKELAND, 2019).
3. VISUALIZAÇÃO E SEPARAÇÃO FÍSICA DAS UNIDADES
A unidade comunicativa é representada pela linha sombreada que aparece como linha de espiral projetada no tubo (figura 3). A unidade natural aparece como sendo efeito homogêneo da transparência reflexiva (figura 6). Já a unidade interativa representa os pontos e a região da similaridade que surge no comprimento interno do tubo no formato de anéis da espiral – essa região se torna visível e delineada na forma de sombra (NETO, 2015).
Nessa verificação, a correlação do formato geométrico e das convergências reflexivas, a partir da região similar no tubo, imprime os mesmos pontos de interação entre espaço, luz, superfície, materiais e campo escuro.
3.1 O QUE SÃO EFEITOS ANAMÓRFICOS?
São processos de transformação, distorção, recombinação, aumento de complexidade e fusões. Os efeitos anamórficos ocorrem naturalmente, mas também de forma induzida, e o conceito de anamorfose aplica-se a qualquer situação em que a base constitutiva transfere suas características para a constituição geral – tal como um fractal, estrutura geométrica complexa cujas propriedades, em geral, repetem-se em qualquer escala. Dada a gama de interpretações que o conceito permite, ele foi adotado por diversas áreas.
Para melhor entendimento serão apresentadas algumas análises comparativas quanto à óptica, que significa “visão’’ e é o ramo da Física que estuda os fenômenos que têm como causa determinante a energia radiante. A óptica explica, a partir das proposições quanto às trajetórias seguidas pela luz, o estudo da natureza constitutiva da luz, as causas dos defeitos de visão, a projeção de imagens e o funcionamento de espelhos, entre outras aplicações.
Figura 1: Base representativa de Maxwell.
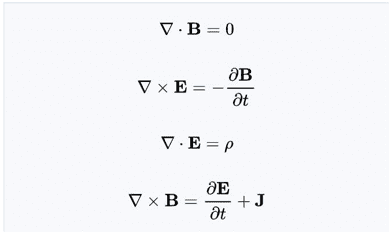
As equações de Maxwell (1862) podem ser divididas em duas grandes variações: (i) grupo “microscópico” que utiliza os conceitos de carga total e corrente total, incluindo as cargas e correntes em níveis atômicos, que comumente são difíceis de se calcular e (ii) grupo “macroscópico” que define os dois novos campos auxiliares que podem evitar a necessidade de ter que se conhecer tais cargas e correntes em dimensões atômicas.
As equações de Maxwell (1862) são chamadas assim em homenagem ao físico e matemático escocês James Clerk Maxwell, publicadas originalmente em um artigo dividido em quatro partes, intitulado On Physical Lines of Force (ou “Acerca das linhas físicas de força”, em português). Maxwell publicou entre 1861 e 1862, podendo as equações serem encontradas sob outras notações matemáticas. A lei da força de Lorentz, sob a forma matemática, também está presente neste artigo.
3.2 BASE MATEMÁTICA DE REFLEXÃO DA LUZ
As resoluções e elucidações das equações de Maxwell (1862) são oriundas dos estudos de Willebrord Snellius e René Descartes. Os estudos indicavam que os raios de luz mudam de direção quando se refletem de uma superfície, movem-se de um meio transparente para outro ou viajam através de um meio cuja composição está mudando continuamente. A lei da reflexão afirma que, no reflexo de uma superfície lisa, o ângulo do raio refletido é igual ao ângulo do raio incidente. Por convenção, todos os ângulos da óptica geométrica são medidos em relação ao normal à superfície – ou seja, a uma linha perpendicular à superfície (FASSARELLA, 2007).
Neste contexto, o raio refletido está sempre no plano definido pelo raio incidente e o normal ao raio incidente na superfície. A lei da reflexão pode ser usada para entender as imagens produzidas por espelhos planos e curvos. Ao contrário dos espelhos, a maioria das superfícies naturais é irregular na escala do comprimento de onda da luz, e como consequência, os raios de luz incidentes paralelos são refletidos em muitas direções diferentes ou difusamente. A reflexão difusa é responsável pela capacidade de ver a maioria das superfícies iluminadas de qualquer posição, já que, os raios atingem os olhos após refletir todas as partes da superfície (SILVA et al., 2012).
Quando a luz que viaja em um meio transparente encontra um limite com um segundo meio transparente (por exemplo, ar e vidro), uma porção da luz é refletida e uma porção é transmitida para o segundo meio. À medida que a luz transmitida se move para o segundo meio, ela muda sua direção de viagem; ou seja, é refratada. A lei da refração (Figura 2), também conhecida como lei de Snell-Descartes, descreve a relação entre o ângulo de incidência (θ1) e o ângulo de refração (θ2), medido em relação à normal, (“linha perpendicular”) à superfície, em termos matemáticos: n1 sin θ1 = n2 sin θ2, onde n1 e n2 são o índice de refração do primeiro e do segundo meios, respectivamente. O índice de refração para qualquer meio é uma constante adimensional igual à razão entre a velocidade da luz no vácuo e sua velocidade nesse meio (FASSARELLA, 2007).
Figura 2: Reflexão e refração segundo a lei de Snell-Descartes.
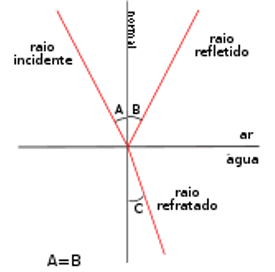
O princípio de Fermat (derivado das leis de reflexão e refração) afirma que a luz viaja entre dois pontos, de forma que o tempo total percorrido seja mínimo. Como a luz viaja em velocidades diferentes por diferentes superfícies, o caminho de menor tempo pode não ser uma linha reta. Em particular, a luz viaja uma distância maior ao passo que possui uma velocidade mais alta. Assim, é possível encontrar o caminho seguido pelo raio de luz (caminho ótico) arrastando o ponto no limite entre as duas superfícies para minimizar o tempo total percorrido, neste contexto, fica estabelecido os mecanismos para dedução da ótica geométrica (MARTINS; SILVA, 2013).
4. ANÁLISE COMPARATIVA E REFERENCIAL DE MODELOS FRACTAIS
Fractais são figuras da Geometria não euclidiana. Um fractal é um objeto geométrico que pode ser dividido em partes, cada uma semelhante ao objeto original. Diz-se que os fractais têm infinitos detalhes e são geralmente auto-similares. Em muitos casos, um fractal pode ser gerado por um padrão repetido, em um processo tipicamente recorrente e iterativo. O termo, criado em 1975 por Benoit Mandelbrot, matemático nascido na Polónia, que descobriu a geometria fractal na década de 70, século XX, também significa “quebrar”.
4.1 LEIS DA REFLEXÃO
As leis da reflexão podem ser analisadas a partir da teoria corpuscular da luz. Trata-se da colisão dos fótons com superfícies espelhadas, de forma análoga à colisão de uma esfera completamente elástica, inclinada a um determinado ângulo, com uma superfície, como se observa na imagem a seguir.
Figura 3: Comparativo entre fótons e similaridade do tubo.

Para fins práticos, nessa análise, a luz funciona como um localizador que imprime a região e os pontos da similaridade entre os cinco sistemas: campo escuro, luz, espaço, tubo e pontos similares. A característica elástica dos fótons indica a relação com pontos de similaridade geométrica.
A similaridade recorrente no tubo de alumínio e os fótons provocam um relacionamento entre eles, criando anéis de cores. É possível verificar dois modelos de interação do fóton com a região similar: um que forma anéis fixos (figura 4) e outro que forma a unidade natural no limite do tubo (figura 7). São dois tipos de diluição: fixa e dinâmica. A região de similaridade entre eles está representada na forma de sombra e linha de espiral, marcada pela diluição do campo escuro. Esse encontro torna visível a unidade natural, comunicativa, indicando que a transferência de informação, nesses níveis, segue orientação das regiões similares.
a) Desenho do campo escuro: O tubo cria uma linha similar por onde o campo escuro pode percorrer essa trilha de orientação, em que as informações geométricas presentes no espaço podem ser vistas e reconhecidas. É possível verificar que é nessa trilha da diluição de campo escuro que a região interativa é impressa.
- b) Desaceleramento de espaço: A linha de campo escuro apresenta características que desaceleram o espaço no limite do tubo, na forma de transparência refletida (unidade natural). Essa análise prioriza a interpretação de que o campo escuro está sendo desenrolado a partir dos pontos de ligações similares de tubo.
Apresentação de anéis:
Anel 1= cor branca.
Anel 2= cores primárias.
Anel 3= cores primárias
Anel 4 = cores primárias
Anel 5= cores primárias
A figura 4, na sequência, ilustra essa elucidação.
Figura 4: Imagens dentro do tubo de alumínio.

A ilustração a seguir mostra o tubo de alumínio utilizado neste experimento.
Figura 5: Tubo de alumínio redondo 30 cm / 3,17 cm × 3,17mm.

As condições de recorrência similar em um tubo de alumínio fornecem ao campo escuro uma trilha de interação com a luz na forma de sombra, em um processo natural de diluição. Esse ponto similar causa uma interatividade modular que se repete nos níveis sutis e físicos consistentes. Essa análise permite também entender e mapear, visualmente, esse efeito na escala microscópica em superfícies.
Ao verificar o comportamento da luz quando projetada em um tubo de alumínio, é possível iniciar a observação e o experimento para entender o campo escuro, que é identificado na ciência atual como sendo a falta de luz.
Nessa verificação, fica evidente um estado de densidade sutil do campo escuro, ao considerar a ocorrência interativa entre a sombra projetada no tubo e os anéis formados no seu interior, e que a linha de campo escuro utiliza as mesmas posições para se orientar e projetar no formato de espiral, apropriando-se dos pontos e da linha de autossimilaridade no tubo.
Considerando que os anéis coloridos apresentam características de padrão fixos sem movimento, e que o estado sutil e físico (rígido) apresenta as mesmas geometrias, os pigmentos no formato de cores também podem ser considerados fixações de escalas. A seguir, a imagem apresenta a unidade natural espalhada em tubo (figura 6).
Figura 6: Unidade natural espalhada em tubo.

Apesar da unidade da transparência (figura 7) concentrar-se no final do tubo, seu espalhamento pode ocorrer em toda a região interna do tubo (figura 6) por ser uma densidade mais baixa. Pode mover-se por toda região interna em uma camada de interatividade mais sutil.
De acordo com essa observação é possível verificar, experimentalmente, que a ausência de luz, ou campo escuro, apresenta características de densidade separadas do espaço. Esse campo escuro segue a orientação dada pela região similar onde a linha sombreada se projeta no tubo (mostrada na imagem 4). Quando é analisado o modelo de sombra, verifica-se a relação desta e o formato do tubo, além do espaço que é ajustado ao formato do tubo, sendo que esse ajustamento pode ser identificado pela linha de sombra. A região espiralada dentro do tudo traz essa forte evidência de que o campo escuro é um estado separado do espaço, logo, com densidades sutis diferentes do espaço, e passam a se comunicar quando suas densidades tornam-se parecidas a partir de uma região de similaridade entre os dois. Assim, o campo escuro precisaria de uma região similar para interagir com o espaço menos denso.
5. UNIDADE COMUNICATIVA
Na observação, o primeiro anel de cor branca, formado no limite final do tubo, concentra e torna visível o efeito de unidade natural de menor densidade, gerando a unidade homogênea transparente – indicando sua menor densidade. Essa unidade se forma no orifício e representa a primeira entrada de luz no tubo de alumínio que, por sua vez, permeia virtualmente os anéis e se move através da via principal similar maior e menor. Essa capacidade de sobrepor tem evidência na densidade baixa, o que significa que essa unidade possui capacidades de adaptações. A evidência interativa entres os dois modelos, anéis de cores e unidade da transparência, ocorre na multiplicidade de trilhas similares presentes nessa unidade.
Na imagem 7, representa-se a unidade de menor densidade capaz de se adaptar com os estados. Essa unidade se movimenta no tubo e permite as trilhas interativas com níveis mais sutis. Ademais, possui multiplicidades de vias em fluxo e é natural, com cor transparente, que se forma e se acumula no início e no limite do tubo.
Figura 7: Unidade de menor densidade.

A seguir é apresentada uma imagem que ilustra a unidade transparente virtualmente espalhada na região do tubo.
Figura 8: Unidade transparente ou unidade adaptativa.

5.1 CONFIRMAÇÕES
Prova-se que o tubo é o formato ideal para esse tipo de apresentação, por reproduzir as condições naturais do raio de luz projetado no espaço. No tubo físico, pode-se verificar o interior do raio de luz e o comportamento do espaço no interior do raio de luz.
Figura 9: Espectro do raio de luz utilizando os pixels de uma tela de TV de LED.

A densidade do campo escuro pode ser identificada a partir do formato geométrico do tubo de alumínio quando na presença da luz, que sensibiliza as regiões similares por onde o campo escuro se projeta, desenrolando em uma orientação no espaço interno do tubo, podendo ser comparado com o raio de luz. Logo, deduz-se que se o campo escuro é uma linha que está sendo desenrolada e apresenta características de densidade, então o campo escuro existe, microscopicamente, como uma estrutura sobreposta na forma de linha enrolada, uma vez que o tubo faria o desenrolamento na base.
A seguir são apresentadas imagens microscópicas ilustrativas com o formato da linha de campo escuro antes do desenrolamento, segundo a análise feita em tubo de alumínio.
Figura 10: Imagens microscópicas ilustrativas.

5.2 RECORRÊNCIA COMUNICATIVA
A recorrência comunicativa ocorre no desenrolamento geométrico do campo escuro, (imagem 4) quando a linha de sombra faz a conexão com espaço invisível, tornando-o visível, ou seja, causando visibilidade às reflexões na forma de unidade natural transparente (essa mesma linha de campo escuro é responsável por delinear e subdividir os anéis presentes nos níveis apresentados na imagem 4)
As soluções de interatividade entre os estados materiais e os espaços mais sutis, aparentemente, podem ser resolvidas com este modelo demonstrado.
5.3 DILUIÇÃO DO CAMPO ESCURO EM SUPERFÍCIE
A sombra obtida no tubo aparece como um estado que localiza os pontos similares por onde ocorre a modulação, a transmissão e a diluição. Para que haja uma interação com o espaço, o campo escuro precisa ser uma densidade separada dele, passando a se orientar a partir do estado de unidade natural e da região de múltiplas similaridades, que também são observadas em superfícies.
Abaixo é apresentada uma imagem ilustrativa de campo escuro sendo desenrolado em superfície, teoricamente em regiões similares, a partir de uma tela luminosa ou superfície refletora.
Figura 11: Campo escuro sendo desenrolado em superfície.

A escala de diluição do campo escuro em superfície ocorre por fases:
Fase 1 – Superfície.
Fase 2 – Rugosidade.
Fase 3 – Fragmentos.
Fase 4 – Fervilhamento.
Fase 5 – Subfases.
Fase 6 – Unidades
5.4 IMAGEM DO CAMPO ESCURO
Se o campo escuro segue uma orientação natural, ou seja, uma das três unidades, através das linhas similares, formando a diluição de campo escuro, logo ele passa a ter um modelo separado do espaço e ganha o formato apresentado na figura 12. Porém, se o campo escuro se desenrola como uma linha, pode-se afirmar que ele tem as características de uma linha enrolada antes do desenrolamento, como mostra a figura abaixo.
Figura 12 – Características de imagem de campo escuro.

São diversos os sistemas que podem ser estudados e entendidos a partir desse formato mas, aqui, o que se pretende é apenas demonstrar que por meio dessa análise em tubo de alumínio, o modelo de imagem do campo escuro fica bastante evidente.
Na sequência, a imagem apresenta um modelo de luz projetado no tubo e seu desenrolamento a partir da sombra espiralada.
Figura 13: Elaborado pelo autor (2019).

Para essa análise, o campo escuro representa a parte escura da imagem acima. Já a sombra, na forma de espiral sendo diluída, representa o estado de desenrolamento do campo escuro, sendo um formato de diluição do campo escuro.
CONSIDERAÇOES FINAIS
Ao longo desta abordagem se percebeu que o campo escuro, ou falta de luz, produz evidências de ser uma densidade separada do espaço. A diluição do campo escuro ocorre quando a luz, o campo escuro e o espaço passam a interagir através da região similar apresentada em tubo de alumínio, que cria níveis de orientação e interação. Experimentalmente, em uma análise descritiva, pode-se notar isso projetando luz em um tubo de alumínio como demonstrado nas imagens deste artigo. Ao observar esses pontos similares, percebe-se que o campo escuro é diluído através da região similar no tubo. Logo, entende-se que o campo escuro, desde que provada sua densidade, passa a ter uma imagem no formato de linha enrolada e sobreposta, como apresentado anteriormente.
REFERÊNCIAS BIBLIOGRÁFICAS
ASKELAND, D. R. Ciência e engenharia dos materiais. São Paulo: Cengage, 2019.
COLLINS, D. L. Anamorphosis and the Eccentric Observer: History, Technique and Current Practice. Leonardo, Vol. 25, n. 2, 1992, p. 179-187.
EXPLICATORIUM Reflexão da luz. 2005. [Internet] Disponível em: <http://www.explicatorium.com/cfq-8/reflexao-da-luz.html>. Acesso em 03.02.2020.
FASSARELLA, L. Lei de Snell generalizada. Rev. Bras. Ensino Fís., v. 29, n. 2, p. 215-224, 2007.
HEINONEN, O.; TAYLOR, P. L. A quantum approach to condensed matter physics. Cambridge University Press, 2002.
KITTEL, C. Introduction to solid state physics. Wiley, 1996.
LUZ, M. L. G. da. Sistemas de Unidades. 2012. Disponível em: <https://wp.ufpel.edu.br/mlaura/2012/09/15/sistemas-de-unidades/>. Acesso em: 01 de fevereiro de 2020.
MANDELBROT, B. Princípio da auto similaridade. Disponível em: <https://blogpai.wordpress.com/principio-da-auto-similaridade-nocoes-de-geometria-fractal/>. Acesso em 12 de dezembro de 2019.
MARTIN, M. C.; MIHALY, L. Solid State physics: problems and solutions. Wiley-Interscience, 1996.
MARTINS, R. A.; SILVA, A. P. B. Princípios da óptica geométrica e suas exceções:
Heron e a reflexão em espelhos. Revista Brasileira de Ensino de Física, v. 35, n. 1, 1605, 2013.
NETO, B. J. Teoria eletromagnética: Parte Clássica. 1º ed. Livraria da Física. 2015.
PATY, M. O conhecimento na física: do invisível segundo a observação ao visível segundo o pensamento. Sci. stud. vol. 8, n. 8. 2010.
REMORTEL, N. V. The nature of natural units. Nature Physics, v. 12, n. 1, 1. 2016.
MAXWELL, J. C. On Physical Lines of Force, 1862.
SADAO, M. Introdução ao Fractal. 2010. Disponível em: <https://www.dm.ufscar.br/~sadao/download/?file=article/fractal.pdf>. Acesso em 07 de janeiro de 2020.
SILVA, O. H. M. et. al. Cad. Bras. Ens. Fís., v. 29, n. 3: p. 1188-1199, 2012.
SNOKE, D.W. Solid State Physics. 2º ed. Cambridge: Cambridge Press, 2020.
VACARIU, G.; VACARIU, M. Rethinking “Dark Matter” within the Epistemologically Different World (EDW) Perspective. In: SMITH, M. Cosmology 2020: The Current State. 1º ed. London: IntechOpen., 2020. cap. 1, p. 1-18.
[1] Iniciado em Ciência da Computação.
Enviado: Agosto de 2020.
Aprovado: Janeiro de 2021.




